大模型- 强化学习-SVM算法与TRPO 中的拉格朗日二次优化--91

目录

• 参考
• 核心思想：拉格朗日对偶与约束优化
• 1. SVM：经典的二次规划问题
• TRPO：迭代中的二次规划子问题

参考

https://gemini.google.com/app/7580b35a3150bf5a

核心思想：拉格朗日对偶与约束优化

在机器学习不同分支中“殊途同归”的经典优化思想，SVM和TRPO都利用了拉格朗日对偶性（Lagrangian Duality）来解决一个带约束的二次优化问题，但它们解决的问题背景和具体实现方式有所不同。

在深入算法之前，我们先简单回顾一下“拉格朗日二次优化”的核心思想。
当我们需要在一个或多个约束条件下，寻找某个目标函数的最小值或最大值时，就遇到了一个约束优化问题
拉格朗日对偶是一种强大的数学工具，它通过引入拉格朗日乘子 (Lagrange Multipliers)，将这个“有约束”的原始问题（Primal Problem）转化为一个“无约束”的对偶问题（Dual Problem）

这个转换的妙处在于：
对偶问题往往更容易求解。
在某些条件下（如KKT条件满足时），对偶问题的解与原始问题的解是等价的。

当目标函数是二次函数（即变量的最高次数为2），并且约束是线性的时候，我们就称之为二次规划 (Quadratic Programming, QP)。SVM和TRPO的核心步骤都涉及求解这样一个问题。

1. SVM：经典的二次规划问题

SVM的目标： 在特征空间中找到一个最大间隔超平面，将两类数据点分得最开。

原始问题（Primal Problem）：
最小化目标：
这里的 是一个关于权重向量 w 的二次项。最小化它等价于最大化间隔 2/∣∣w∣∣
约束条件对于所有样本 i。
这个约束保证了所有样本点都被正确分类，并且位于间隔边界之外。这是一个线性约束
这是一个非常标准的二次规划问题。

如何使用拉格朗日对偶解决？
构建拉格朗日函数： 引入拉格朗日乘子 ，将约束条件融入目标函数中：

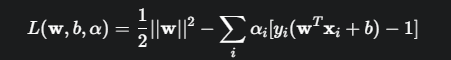
求解对偶问题（Dual Problem）
通过对 w 和 b 求偏导并令其为零，可以消去这两个原始变量，最终得到一个只关于乘子 α 的最大化问题：

最大化目标：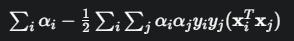
约束条件：

这个对偶问题依然是一个二次规划问题，但它的变量是拉格朗日乘子 αi。它的优势在于
引入核技巧：目标函数中的内积 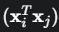可以被核函数替代，轻松地将SVM扩展到非线性分类。
稀疏解大部分 αi会等于0，只有少数不为0，这些对应的样本点就是“支持向量”，决定了最终的超平面。

TRPO：迭代中的二次规划子问题

TRPO的目标： 在保证新策略与旧策略不会相差太远的前提下，最大化策略的性能提升。

原始问题（在每次迭代中）：
最大化目标：
这是一个衡量策略提升的“代理优势函数”
约束条件：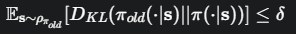
这个约束保证了新旧策略的KL散度在一个很小的“信任区域” δ 内

这个问题的目标函数和约束都非常复杂，难以直接优化。
如何近似并使用拉格朗日思想？

TRPO的关键一步是局部近似：
将目标函数在旧策略参数 θold处进行一阶泰勒展开（线性近似）。
将KL散度约束在θold处进行二阶泰勒展开（二次近似）。

这样，在每次迭代中，TRPO实际求解的是下面这个近似后的二次约束优化问题：
目标：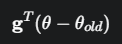
约束条件：

这里的 g 是策略梯度，F 就是我们上一问中提到的费雪信息矩阵（Hessian的近似）
这个问题同样可以通过拉格朗日对偶理论来求解。其KKT条件给出了最优解的形式，最终推导出更新步长的计算公式，其中涉及到求解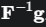 。TRPO使用共轭梯度法高效地计算这一项，而避免了直接求逆。

SVM和TRPO都运用了拉格朗日二次优化的框架来解决各自领域的核心问题。
SVM 将其作为一个一次性的、精确的工具来求解一个定义明确的几何问题（最大化间隔）。
TRPO 则将其作为一种迭代的、近似的手段，在每一步更新中为策略的改进方向和幅度提供一个稳定、可靠的理论依据。