大模型- 强化学习-GPTQ量化算法与TRPO中的海森矩阵--90
参考
https://g.co/gemini/share/6804174d7c5f
内容背景
海森矩阵在GPTQ与TRPO中的应用:关联性深度解析
在机器学习领域,优化算法的演进日新月异,其中,二阶优化方法因其能利用损失函数的曲率信息而备受关注。
海森矩阵(Hessian Matrix)作为二阶导数的泛化,在诸多先进算法中扮演着核心角色。本文将深入剖析海森矩阵在GPTQ量化算法和TRPO强化学习算法中的应用,阐述其内在关联,并对海森矩阵本身进行详尽的讲解。
海森矩阵详解:洞察函数曲率的窗口
海森矩阵是一个方阵,由一个多变量函数的二阶偏导数构成。对于一个定义域为\(\mathbb{R}^n\),输出为实值的函数 f(x),其海森矩阵 H 在点 x 处的定义如下:
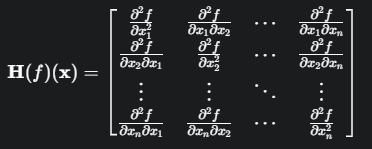
核心作用:
描述局部曲率: 海森矩阵的本质是描述了函数在某一点附近的局部曲率。梯度(一阶导数)指明了函数值增长最快的方向,而海森矩阵则揭示了函数在该方向上的“弯曲程度”。
判断极值点: 在驻点(梯度为零的点),海森矩阵的性质可以帮助我们判断该点是局部最小值、局部最大值还是鞍点。
正定矩阵: 所有特征值为正,对应局部最小值。
负定矩阵: 所有特征值为负,对应局部最大值。
不定矩阵: 特征值有正有负,对应鞍点。
在机器学习中,我们通常处理的是高维的损失函数,海森矩阵为我们提供了一个理解和优化复杂损失函数曲面的有力工具。
GPTQ量化算法:利用海森矩阵进行精准“瘦身”
GPTQ(Generative Pre-trained Transformer Quantization) 是一种先进的训练后量化(Post-Training Quantization, PTQ)(已经是局部最小)算法,旨在将大型语言模型的权重从高精度(如FP16)压缩到低精度(如INT4),同时最大程度地减少精度损失。
在GPTQ中,量化过程被视为一个逐层、逐个权重进行的优化问题。其核心思想是,在量化某个权重时,需要对其他未量化的权重进行微调,以补偿量化所带来的误差。海森矩阵在此过程中扮演了“误差分配”的关键角色。
“一张吸满水的海绵 从左往右 把水 挤掉”
具体来说,GPTQ的目标是最小化量化前后模型输出的差异。这个差异可以用一个二次型来近似,而这个二次型的核心就是损失函数关于权重的海森矩阵。
已经是局部最小,一阶项=0
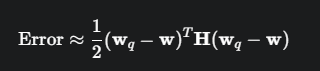
其中,w 是原始权重,wq是量化后的权重,H 是海森矩阵。
GPTQ利用海森矩阵:
确定量化顺序: GPTQ通过分析海森矩阵的逆,来决定哪些权重对模型的性能影响较小,可以优先进行量化。具体来说,它会选择那些即使被量化,也能通过调整其他权重来轻松补偿其误差的权重。
权重更新: 在量化一个权重后,GPTQ利用海森矩阵的逆来计算对剩余未量化权重的最佳更新量,从而弥补因量化引入的精度损失。这确保了每一步量化都是在最小化对模型整体性能影响的前提下进行的。
简而言之,GPTQ将海森矩阵作为模型参数重要性的衡量标准和误差补偿的指导。它利用二阶信息来更智能地进行权重的舍入和调整,而不是简单地进行最近邻取整。
TRPO算法:借助海森矩阵构建“信任区域”
TRPO(Trust Region Policy Optimization) 是一种强化学习中的策略优化算法,旨在解决传统策略梯度(PG)方法中步长选择困难、容易导致策略崩溃的问题。
海森矩阵的应用:
TRPO的核心思想是在每次策略更新时,都定义一个“信任区域”(Trust Region)。在这个区域内,对目标函数的近似是可靠的,因此可以安全地进行策略更新。这个信任区域的大小由新旧策略之间的KL散度(Kullback-Leibler divergence)来衡量。
为了在满足KL散度约束的同时最大化策略提升,TRPO在推导中对KL散度进行了二阶泰勒展开,此时海森矩阵便自然而然地出现了。
具体来说,TRPO使用的是KL散度关于策略参数\(\theta\)的海森矩阵,这个矩阵在强化学习中通常被称为费雪信息矩阵(Fisher Information Matrix, FIM),它可以被看作是海森矩阵的一种特殊形式或近似。
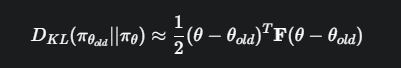
其中,F 是费雪信息矩阵。
TRPO利用海森矩阵(FIM):
定义信任区域: 费雪信息矩阵定义了策略参数空间中的一个度量,用于衡量策略变化的“真实”大小。TRPO利用它来构建一个椭圆形的信任区域,确保更新后的策略不会与旧策略相差太远。
计算更新方向: TRPO的更新方向是通过求解一个约束优化问题得到的,其中涉及到费雪信息矩阵的逆。然而,对于大型神经网络策略,直接计算和求逆巨大的费雪信息矩阵是极其耗费计算资源的。因此,TRPO巧妙地采用了共轭梯度法(Conjugate Gradient Method),在不显式计算整个矩阵的情况下,高效地计算出所需的更新步长(即\(\mathbf{F}^{-1}\mathbf{g},其中\mathbf{g}\)是策略梯度)。
GPTQ与TRPO中海森矩阵应用的关联性分析
尽管GPTQ和TRPO应用于截然不同的领域(模型压缩 vs. 强化学习),但它们在使用海森矩阵的底层逻辑上存在着深刻的关联性:
共同的理论基础:二阶近似
两个算法都利用了泰勒展开的二阶近似思想。GPTQ用它来近似量化误差,TRPO用它来近似策略间的KL散度。这使得它们能够超越只考虑梯度(一阶信息)的算法,通过捕捉函数的局部曲率信息,做出更稳健、更精确的优化决策。
核心作用:指导优化方向和步长
在两个算法中,海森矩阵(或其近似FIM)都充当了优化过程的“导航仪”。在GPTQ中,它指导如何分配和补偿量化误差。在TRPO中,它定义了策略参数更新的安全边界(信任区域),并帮助计算出在该边界内最有效的更新方向和大小。
面临的共同挑战:计算复杂性
对于现代深度学习模型,其参数量巨大,导致海森矩阵的维度极高,直接计算和存储、求逆都是不现实的。因此,两个算法都采用了近似或高效的计算策略。
GPTQ 通过一系列优化,如延迟更新和Cholesky分解,来高效地处理海森矩阵的计算。
TRPO 则通过共轭梯度法,巧妙地规避了对整个费雪信息矩阵的显式计算和求逆,转而计算其与梯度向量的乘积,极大地提升了算法的可行性。
总结来说,GPTQ和TRPO都将海森矩阵作为一种度量工具,用于衡量参数空间中微小变动对某个目标函数(量化误差或策略分布)的影响。通过利用海森矩阵提供的曲率信息,它们得以实现比一阶方法更稳定和高效的优化。它们之间的关联性,体现了二阶优化思想在不同机器学习子领域中解决核心挑战的普适性和强大能力。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号