大模型- 强化学习-GAE--87

目录

参考

https://g.co/gemini/share/e45888162cfb
https://newfacade.github.io/notes-on-reinforcement-learning/13-gae.html

内容

先理解一下 真实值与期望值
真实值是无偏的 但是方差很大

泛化优势估计 (Generalized Advantage Estimation, GAE)
在现代强化学习，特别是策略梯度方法（如 PPO, TRPO）中，几乎成为标配的关键技术。
理解 GAE 的核心是理解偏差-方差权衡 (Bias-Variance Tradeoff)。

Generalized Advantage Estimation (GAE) described an advantage estimator, with two separate parameters γ and λ, both of which contribute to the bias-variance tradeoff when using an approximate value function.

There are several different related expressions for the policy gradient, which have the form
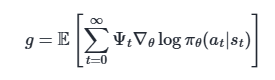
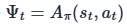image
image

imageyields almost the lowest possible variance, though in practice, the advantage function is not known and must be estimated.

优势估计的“两难困境”

Actor-Critic 方法中，我们知道了策略更新需要一个“指导信号”——优势函数 A(s, a)。但如何精确地估计这个优势函数，一直是个难题。我们之前接触过两种主要的估计方法，它们各有优劣，形成了一个两难的局面。

REINFORCE (高方差，无偏差)

REINFORCE 算法（带有基线 V(s)）使用蒙特卡洛 (Monte Carlo) 的方式来估计优势：
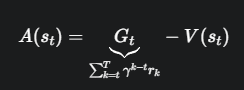
image

  • 优点 (无偏差 Unbiased)：它使用了从 t 时刻开始直到回合结束所有的真实奖励，是对未来回报的无偏估计。从理论上讲，它的期望是准确的。
  • 缺点 (高方差 High Variance)：G_t 的值依赖于一长串的动作和状态转移，其中任何一步的随机性都会累积起来，导致 G_t 的值波动非常大。这使得训练过程很不稳定。

基础 Actor-Critic (低方差，有偏差)

基础的 Actor-Critic 方法使用时序差分 (TD) 的方式，只往后看一步：
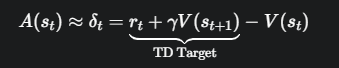
image

  • 优点 (低方差 Low Variance)：优势的计算只依赖于一步的奖励 r_t 和下一个状态的价值估计 V(s_{t+1})，随机性来源少，所以估计值相对稳定。
  • 缺点 (有偏差 Biased)：它严重依赖于 Critic 对下一个状态的价值估计 V(s_{t+1})。如果 Critic 当前的估计不准（在训练早期几乎肯定不准），这个不准确性（偏差）就会被引入到优势估计中，从而指导 Actor 错误地更新。

总结一下这个困境：
想得到准确（无偏）的估计，就得承受不稳定（高方差）的代价 (REINFORCE)。 G_t的计算
想得到稳定（低方差）的估计，就得承受不准（有偏差）的风险 (TD Actor-Critic)。 critic输出TD_error

有没有一种方法可以让我们在这两者之间自由地权衡，找到一个最佳的平衡点呢？GAE 就此诞生。

GAE 的核心思想与公式

GAE 巧妙地通过引入一个新参数 λ (lambda)，对多步 TD 误差进行指数加权平均，从而统一了上述两种估计方法。

Let V be an approximate value function.
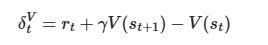
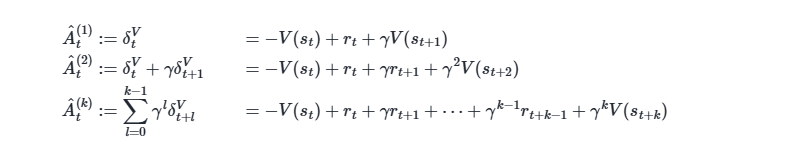
image
image

上面的k步估计 指数加权平均
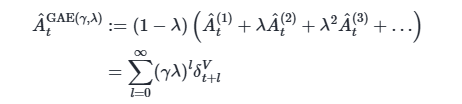
image

two notable special cases of this formula, obtained by setting
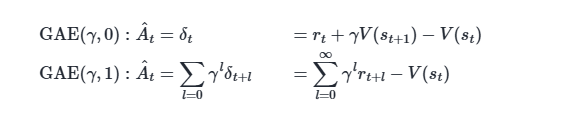
image

结论：通过调整 λ 在 0 和 1 之间，我们可以在“完全信任 Critic”和“完全不信 Critic，只信真实奖励”之间进行平滑过渡，从而为特定的任务找到最佳的平衡点。在实践中，λ 通常被设置为 0.9 到 0.99 之间的一个值（如 0.95），这被证明在很多任务上效果都很好。

GAE 的代码实现

上面的无穷级数公式在代码中并不好实现。幸运的是，它有一个等价的、更实用的递归形式。
我们在一个回合结束后，收集了所有的 (奖励 r_t, 价值 V(s_t))。然后，我们从后往前遍历这些数据来计算 GAE 优势。
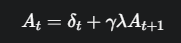
image
直观理解：在 t 时刻的优势，等于当前这一步的 TD 误差 δ_t，再加上由 γ 和 λ 共同折扣的下一步的优势 A_{t+1}。

代码实现逻辑 (通常放在 finish_episode 或类似函数中)
假设我们已经在一个回合中收集了 rewards 列表和 values 列表

# GAE 参数
GAMMA = 0.99
LAMBDA = 0.95 # GAE 的核心参数 λ

# ... 在 finish_episode() 内部 ...

gae = 0 # 初始化 A_T = 0
advantages = [] # 存储每个时间步的 GAE 优势

# 从后往前遍历数据 (从 t=T-1 到 t=0)
for t in reversed(range(len(rewards))):

    # 1. 计算 TD 误差 δ_t = r_t + γ * V(s_{t+1}) - V(s_t)
    # 对于最后一步，V(s_{t+1}) = 0
    if t == len(rewards) - 1:
        next_val = 0 # 终止状态的价值为0
    else:
        next_val = values[t+1] # Critic 对下一个状态的价值估计

    delta = rewards[t] + GAMMA * next_val - values[t]
    
    # 2. 计算 GAE 优势 A_t = δ_t + γ * λ * A_{t+1}
    # 上一步计算出的 gae 就是 A_{t+1}
    gae = delta + GAMMA * LAMBDA * gae
    
    # 将计算好的当前步的优势 A_t 插入到列表的前端
    advantages.insert(0, gae)

# --- 后续步骤 ---
# 此时，`advantages` 列表中就包含了每个时间步的 GAE 优势值
# 1. Actor 的损失: policy_loss = -log_prob * advantage
# 2. Critic 的训练目标:
#    Critic 仍然需要学习去预测真实回报 G_t，而不是优势 A_t。
#    G_t 可以通过 A_t 和 V(s_t) 计算得出： G_t = A_t + V(s_t)
#    returns = advantages + values
# 3. Critic 的损失: value_loss = MSE(V(s_t), G_t)

总结

GAE 旨在解决策略梯度方法中优势估计的偏差-方差权衡问题。
通过引入参数 λ，对多步 TD 误差进行指数加权平均，灵活地融合了蒙特卡洛方法（高方差、无偏）和单步 TD 方法（低方差、有偏）的优点。
λ 的作用：λ 是一个控制旋钮。λ=0 等价于 TD，λ=1 等价于蒙特卡洛。
在代码中，通常采用一个高效的从后往前的递归方式来计算 GAE 优势。
GAE 是现代高性能 Actor-Critic 算法（如 PPO）的基石，是一项非常重要和实用的技术。

posted @ 2025-07-16 17:35  jack-chen666  阅读(303)  评论(0)    收藏  举报