大模型- 强化学习-策略梯度方法（Policy Gradient）log-derivative trick--86

想象一下，你是一位国王，想让你的弓箭手们射箭射得更准。这里的“更准”就是我们要最大化的目标 J(θ)，而 θ 就是你给弓箭手们的“指导方针”（比如，往哪个方向瞄准，用多大的力气等等）。
我们想调整这个“指导方针” θ，让所有弓箭手射出的箭靶得分的期望（平均分）最高。

J(θ) = E[R(τ)]

J(θ): 指导方针 θ 的好坏程度（所有可能射箭路径的平均分）。
θ: 你的指导方针。
τ: 一次完整的射箭行为（从瞄准到射中靶子），我们称之为一条“轨迹”。
R(τ): 这一条轨迹最终的得分（比如10环、5环或者脱靶）。
$E[...] $: 代表“期望”，也就是平均值。我们需要考虑所有可能的射箭轨迹，然后计算它们的平均分。

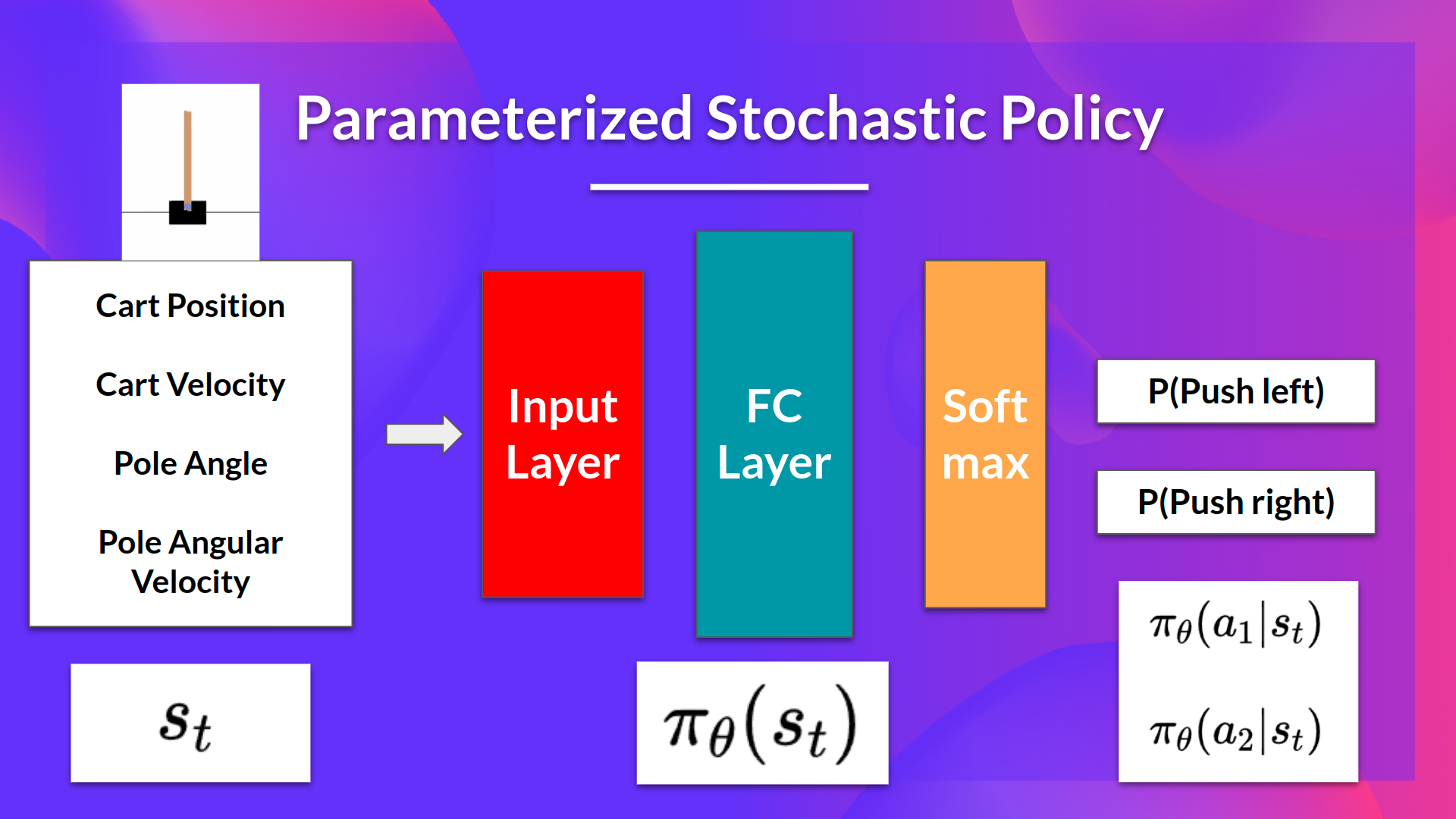
问题来了，你作为国王，并不知道“指导方针 θ”和“最终得分 R(τ)”之间精确的数学关系

这就好像你面对一个黑盒子：
输入：你的指导方针 θ。
黑盒子内部：弓箭手根据你的方针射出一箭（这个过程有随机性，每次射的轨迹 τ 都可能不一样）。
输出：这次射箭的得分 R(τ)。

我们想用梯度上升法来优化，就需要计算梯队 ∇θJ(θ)，
也就是“当我稍微调整一下指导方针 θ，平均分 J(θ) 会怎么变化？”

直接对 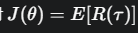求导，就像是隔着一个黑盒子（并且这个黑盒子还带随机性）去求导，非常困难。因为平均分 R(τ) 不直接是 θ 的函数，而是通过一个随机的射箭过程 τ 间接关联的。

先回顾一下背景

The objective function outputs the expected cumulative reward:

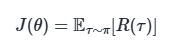
Policy-gradient is an optimization problem: we want to find the values of
that maximize our objective function 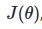, so we can use gradient-ascent:

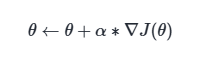
However, there are two problems with computing the derivative of ，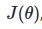

继续回到主题，
“log-derivative trick”魔法登场

这个魔法的精髓在于，它巧妙地把我们头疼的求导对象，从“黑盒子”的外部（期望 E）搬到了“黑盒子”的内部。

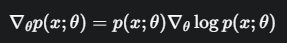
别被公式吓到，我们来分解一下这个魔法的步骤：

首先，我们把期望 E[R(τ)] 写成更具体的数学形式：积分（或求和）。它等于把所有可能轨迹的“（得分）x（该轨迹出现的概率）”加起来。

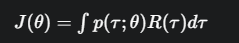
对这个积分求导

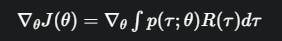
交换积分和求导,
我们可以把求导符号 ∇θ放到积分里面去（在大多数情况下数学上是允许的）

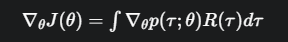
但我们依然很头疼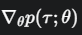，这一项不好处理

施展“log”魔法
我们对 p(τ;θ) 变个戏法，乘以它再除以它，这显然不改变任何东西

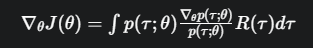
神奇的事情发生了
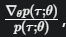这正好是微积分里 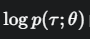的导数！

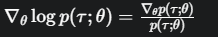
把这个结果代换回去：

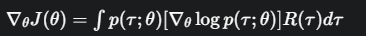
变回期望形式

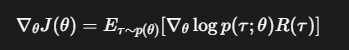
对比一下施法前后的变化：

施法前 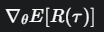（求导在期望外面，很难搞）
施法后 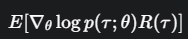（求导在期望里面，变得可行了！）

为什么说变得可行了呢？
可计算了:我们不需要知道那个“黑盒子”内部复杂的函数了。我们只需要能计算 logp(τ;θ) 的梯度就行。在强化学习里，这个 p(τ;θ) 就是我们的策略网络，它的形式是已知的，所以求导很方便。
可以用采样来估算了:这个最终的期望形式，意味着我们可以让弓箭手们（我们的智能体）实际去射很多次箭，得到一堆轨迹样本 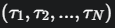和它们对应的得分 。然后用这些样本的平均值来近似整个梯度：

一个绝妙的比喻

这个魔法就像是：
之前：你站在山顶，想知道山脚下哪条路能让你走得最远（收益最大）。但你视野被浓雾（随机性）遮挡，根本看不清路和终点的关系。
施展魔法后：你不用站在山顶看了。你派了很多探险家（采样）下山去走不同的路。每个探险家回来后，你只问他们两个问题：

“你的行走日志（logp(τ;θ)）是怎么写的？” （这条路在你当前指导方针下出现的概率的对数）
“你走了多远（R(τ)）？”

然后，你重点分析那些走得远（R值高）的探险家的行走日志。你会调整你的“指导方针” θ，使得这些“好日志”里记录的行为，在未来出现的概率更大（通过 ∇ θlogp 来调整）。

对于那些走得近甚至掉坑里（R值低）的探险家，你就调整方针，让他们日志里记录的行为概率更小。

总结一下“log-derivative trick”的魔法本质：

它是一个数学工具，巧妙地将对一个期望值的求导，转化为了对一个期望内部的对数概率的求导。

这使得我们能够绕开对复杂、未知或随机过程直接求导的难题，从而可以通过实际采样的方式，来估计梯度，并优化我们的策略。
这就是强化学习中策略梯度方法（Policy Gradient）的核心魔法。