大模型- 强化学习-策略梯度 (Policy Gradients)--84

目录

• 参考
• 内容
  • 为什么要直接学习策略？
  • 核心思想：参数化策略与目标函数
  • 数学核心：策略梯度定理
• REINFORCE 算法：一种简单的实现
  • 代码解读 (以CartPole为例)
  • 总结与展望
• 完整代码

参考

https://gemini.google.com/app/247cc5d3d5bad7de
https://newfacade.github.io/notes-on-reinforcement-learning/11-policy.html
这是强化学习中与我们之前学习的 Q-learning 和 DQN（价值方法）并列的另一大类核心方法

内容

思想转变：从“学习价值”到“直接学习策略”

首先，我们必须理解策略梯度方法与DQN的根本区别。

DQN (价值方法): 它的核心是学习一个价值函数 Q(s, a)。它费尽心思计算出在某个状态 s 下，做某个动作 a 能有多好。学好了Q函数后，策略是“派生”出来的：在每个状态，选择那个能让Q值最大的动作（argmax_a Q(s, a)）。这是一种间接学习策略的方式。 -- 总结太到位了！！

策略梯度 (PG) 方法: 它跳过了计算价值的中间环节，直接去学习一个策略函数 π(a|s)。这个策略函数本身就是一个网络，它的输入是状态 s，输出是每个动作被选择的概率。我们直接通过训练，让这个策略函数变得越来越好。这是一种直接学习策略的方式。 -- 太棒了 ！策略函数 π(a|s) 是一个概率分布！

为什么要直接学习策略？

直接学习策略有几个非常重要的优势：

• 支持随机策略 (Stochastic Policy): 策略网络的输出是概率。这在某些场景下是必须的。比如在“石头剪刀布”游戏中，最优策略就是随机出拳；而在一个迷宫中，如果两个方向一样好，随机选择可以避免卡在原地。DQN的贪心策略是确定性的，无法学习这种随机性。
• 能处理连续动作空间: 想象一下控制一个机器人的关节角度，动作是连续的（比如从0°到180°）。DQN在这种情况下几乎无法工作，因为它无法对无限个动作去计算 max_a Q(s, a)。而策略梯度可以很好地处理，比如让网络输出一个高斯分布的均值和方差，然后从中采样一个动作。-- 支持输出连续空间的action
• 收敛可能更平滑: 有时价值函数 Q(s, a) 的形式非常复杂，但最优策略 π(a|s) 可能很简单。直接学习一个简单的策略会比学习一个复杂的价值函数更容易，训练过程可能更稳定。

核心思想：参数化策略与目标函数

策略梯度(GP)方法将策略表示为一个带有参数 θ 的函数 π(a|s; θ)，这里的 θ 就是神经网络的权重。
策略 π(a|s; θ): 一个神经网络，输入是状态 s，输出一个动作的概率分布。
目标: 找到一组最优参数 θ*，使得由该策略产生的期望总回报最高。

我们定义一个目标函数 J(θ)，它代表了使用策略 π_θ 时，我们能获得的期望总回报。

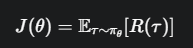
这里的 τ (tau) 代表一个完整的轨迹（episode），R(τ) 是这个轨迹的总回报。我们的目标就是通过调整 θ 来最大化 J(θ)。

一个完整的轨迹（episode）？
一部电影从头看到结尾，一盘游戏超级玛丽玩到结束，一局围棋或者象棋游戏

数学核心：策略梯度定理

为了用梯度上升（Gradient Ascent）来最大化 J(θ)，我们需要计算它的梯度 ∇_θ J(θ)。直接对这个期望求导很困难，但通过一个被称为“log-derivative trick”的数学魔法，我们可以得到一个非常优美的结果，这就是策略梯度定理 (Policy Gradient Theorem)：

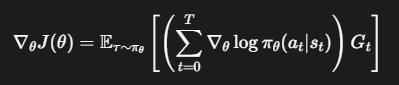
π_θ(a_t|s_t): 在状态 s_t 时，根据我们当前的网络，选择动作 a_t 的概率。
log π_θ(a_t|s_t): 对这个概率取对数。取对数是为了计算方便，不改变梯度的方向。
∇_θ log π_θ(a_t|s_t): 这个对数概率对参数 θ 的梯度，它指向一个方向，如果沿着这个方向更新 θ，那么未来再次遇到状态 s_t 时，选择动作 a_t 的概率就会增加。
未来回报 (Return)。它代表从时间步 t 开始，直到这个回合结束，我们所获得的累积折扣奖励总和。G_t = r_t + γr_{t+1} + γ^2r_{t+2} + ...。这个值衡量了动作 a_t 到底“好不好”。

公式的直观含义:
遍历一个回合中的每一步 t，计算其未来回报 G_t。
如果 G_t 是一个很大的正数（意味着在 s_t 做的动作 a_t 带来了很好的长期结果），我们就让 θ 沿着 ∇_θ log π_θ(a_t|s_t) 的方向更新。这会提高未来在 s_t 选择 a_t 的概率。
如果 G_t 是一个负数或很小的正数（意味着动作 a_t 带来了糟糕的结果），我们就让 θ 沿着梯度的反方向更新，这会降低未来在 s_t 选择 a_t 的概率。
简单来说，就是 “好的行为，使其出现的概率增加；坏的行为，使其出现的概率降低”。

REINFORCE 算法：一种简单的实现

REINFORCE 算法是策略梯度定理最直接的一种实现。它采用蒙特卡洛 (Monte Carlo) 的方式，即必须等待一个完整的游戏回合（episode）结束后，才能进行学习和更新。

初始化策略网络 π(a|s; θ)
循环很多个回合：

• 用当前的策略网络 π_θ 与环境交互，玩完一整个回合。同时，保存好这个回合中所有的 (状态, 动作, 奖励)。
• 回合结束后，从最后一步 T 倒推到第一步 0，为每一步 t 计算它的未来回报 G_t。
• 根据策略梯度公式计算梯度，并更新网络参数 θ：
  
  (其中 α 是学习率)
• 清空保存的轨迹数据，开始新的回合。

代码解读 (以CartPole为例)

看一下 REINFORCE 算法在代码层面是如何实现的，并与DQN进行对比。

1. 策略网络 (Policy Network)

import torch.nn as nn
import torch.nn.functional as F

class Policy(nn.Module):
    def __init__(self):
        super(Policy, self).__init__()
        self.fc1 = nn.Linear(4, 128)
        self.dropout = nn.Dropout(p=0.6)
        self.fc2 = nn.Linear(128, 2) # 输出层大小为动作数量

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.dropout(x)
        # 关键区别！使用 Softmax 将输出转换为概率分布
        action_scores = self.fc2(x)
        return F.softmax(action_scores, dim=1)

与DQN网络的最大区别: 在 forward 函数的最后，我们使用了 F.softmax。DQN的输出是原始的Q值，而策略网络的输出必须是一个合法的概率分布，即所有动作的概率加起来等于1。

2. 动作选择 (select_action)

from torch.distributions import Categorical

def select_action(state):
    # state是当前状态
    probs = policy_network(state) # 得到动作的概率，例如 [0.7, 0.3]
    
    # 关键区别！从概率分布中采样
    m = Categorical(probs)
    action = m.sample() # 根据概率采样一个动作
    
    # 保存该动作的对数概率，用于后续计算损失
    policy_network.saved_log_probs.append(m.log_prob(action))
    
    return action.item()

与DQN的 select_action 完全不同:
这里没有 ε-greedy。
我们根据网络输出的概率 probs 创建一个分类分布 (Categorical Distribution)。
我们从这个分布中 .sample() 来得到一个动作。如果 probs=[0.7, 0.3]，那么我们有70%的概率采样到动作0，30%的概率采样到动作1。
最重要的一步是保存 m.log_prob(action)，也就是 log π_θ(a|s)，因为这是计算梯度所必需的。

3.训练与更新 (finish_episode)

def finish_episode():
    R = 0
    policy_loss = []
    returns = [] # 存储每个时间步的未来回报 G_t
    
    # 从后往前计算每个时间步的未来回报 G_t
    for r in policy_network.rewards[::-1]:
        R = r + GAMMA * R
        returns.insert(0, R)
        
    # 标准化回报（非常重要的技巧，可以稳定训练）
    returns = torch.tensor(returns)
    returns = (returns - returns.mean()) / (returns.std() + 1e-6)
    
    # 计算损失函数
    for log_prob, R in zip(policy_network.saved_log_probs, returns):
        policy_loss.append(-log_prob * R) # 损失函数的核心
        
    optimizer.zero_grad()
    loss = torch.cat(policy_loss).sum() # 将所有步的损失加起来
    loss.backward() # 反向传播
    optimizer.step()
    
    # 清空数据，为下一回合做准备
    del policy_network.rewards[:]
    del policy_network.saved_log_probs[:]

计算回报 G_t: 代码从后往前遍历奖励，高效地计算出每一步的折扣回报 G_t。
标准化回报: 这是一个非常关键的实践技巧。将回报G_t标准化（减去均值，除以标准差）可以显著降低方差，使训练更稳定。它不改变梯度的期望方向，但能控制梯度的大小。
计算损失:
policy_loss.append(-log_prob * R) 完美地对应了策略梯度的思想。
为什么是负号？ 因为优化器（Optimizer）通常是做梯度下降来最小化 (minimize) loss。而我们的目标是梯度上升来最大化 (maximize) log_prob * G_t。因此，最小化 -log_prob * G_t 就等价于最大化 log_prob * G_t。
最终的 loss 是一个回合中所有时间步损失的总和。

总结与展望

REINFORCE 算法非常优雅地实现了策略梯度的基本思想。但它也有一个显著的缺点：
高方差 (High Variance): 因为更新依赖于一整个回合的（随机）回报 G_t，这个回报值的波动可能非常大，导致梯度估计很不稳定，训练过程震荡且缓慢。
这个问题引出了后续更高级的策略梯度方法，例如 Actor-Critic，它会学习一个价值函数（Critic）来辅助策略网络（Actor）的训练，用一个更稳定的“优势函数” A(s, a) 来替代噪声很大的 G_t，从而大幅降低方差。这是您未来学习路径上非常重要的一步。

完整代码

import gym
from collections import deque
env = gym.make('CartPole-v1')
env.reset(seed=1)
env.observation_space.shape[0], env.action_space.n


import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim


class Policy(nn.Module):
    """MLP"""
    def __init__(self):
        super(Policy, self).__init__()
        self.affine1 = nn.Linear(4, 128)
        self.dropout = nn.Dropout(p=0.6)
        self.affine2 = nn.Linear(128, 2)

        self.saved_log_probs = []
        self.rewards = []

    def forward(self, x):
        x = F.relu(self.affine1(x))
        x = self.dropout(x)
        x = F.relu(x)
        action_scores = self.affine2(x)
        return F.softmax(action_scores, dim=1)  # 转化成概率


policy = Policy()
optimizer = optim.Adam(policy .parameters(), lr=1e-2)


import numpy as np
from torch.distributions import Categorical


def select_action(state):
    state = torch.from_numpy(state).float().unsqueeze(0)
    probs = policy(state)
    m = Categorical(probs)
    action = m.sample()
    policy.saved_log_probs.append(m.log_prob(action))
    return action.item()


gamma = 0.99


def finish_episode():
    R = 0
    policy_loss = []
    eps = np.finfo(np.float32).eps.item()
    returns = deque()
    
    for r in policy.rewards[::-1]:
        R = r + gamma * R
        returns.appendleft(R)
    returns = torch.tensor(returns)
    returns = (returns - returns.mean()) / (returns.std() + eps)
    for log_prob, R in zip(policy.saved_log_probs, returns):
        policy_loss.append(-log_prob * R)
    optimizer.zero_grad()
    policy_loss = torch.cat(policy_loss).sum()
    policy_loss.backward()
    optimizer.step()

    del policy.rewards[:]
    del policy.saved_log_probs[:]


from itertools import count


def main():
    running_reward = 10
    for i_episode in count(1):
        state, _ = env.reset()
        ep_reward = 0
        for t in range(1, 10000):
            action = select_action(state)
            state, reward, done, _, _ = env.step(action)
            policy.rewards.append(reward)
            ep_reward += reward
            if done:
                break
        running_reward = 0.05 * ep_reward + (1 - 0.05) * running_reward
        finish_episode()
        if i_episode % 10 == 0:
            print('Episode {}\tLast reward: {:.2f}\tAverage reward: {:.2f}'.format(i_episode, ep_reward, running_reward))
        if running_reward > env.spec.reward_threshold:
            print("Solved! Running reward is now {} > {}".format(running_reward, env.spec.reward_threshold))
            break
    torch.save(policy.state_dict(), "policy.pth")


def eval_model():
    policy.load_state_dict(torch.load("policy.pth"))
    policy.eval()  # Switch to evaluation mode
    
    env = gym.make('CartPole-v1', render_mode='human')  # 设置render_mode为'human'以显示画面

    for i in range(5): # 跑5个回合看看效果
        state, _ = env.reset()
        for t in range(500): # CartPole-v1最多500步
            env.render() # 渲染画面
            
            with torch.no_grad(): # 在评估时不需要计算梯度
                # 对于策略梯度方法
                probs = policy(torch.from_numpy(state).float().unsqueeze(0))
                action = probs.max(1)[1] # 直接选择概率最大的动作

                # 对于DQN方法
                # q_values = policy_network(torch.from_numpy(state).float().unsqueeze(0))
                # action = q_values.max(1)[1] # 直接选择Q值最大的动作
                
            state, reward, done, _, _ = env.step(action.item())
            
            if done:
                print(f"Episode {i+1} finished after {t+1} timesteps")
                break

    env.close()
if __name__ == '__main__':
    # main()
    eval_model()