大模型-qwen3 RoPE旋转位置编码详细解读-69
旋转位置编码(RoPE)是当前大语言模型(如 Llama, Qwen, Mixtral)中事实上的标准技术。要完全理解它,我们非常有必要回顾一下位置编码技术的发展历程,这能帮助我们明白 RoPE 到底解决了什么痛点,以及它为什么如此巧妙。
我们将分两大部分来详细解读:
位置编码技术的发展简史:从 Transformer 的诞生到现在,我们是如何表示位置信息的。
Qwen3 RoPE 代码深度解析:逐行分析您提供的代码,理解其数学原理和实现细节。
第一部分:位置编码技术发展简史
为什么需要位置编码?
Transformer 模型的核心是自注意力机制(Self-Attention),它让每个词(Token)都能关注到句子中的其他所有词。但这个机制有一个天生的“缺陷”:置换不变性 (Permutation Invariance)。也就是说,它把输入看作一个无序的“词袋”,无法感知到单词的顺序。句子 "猫追老鼠" 和 "老鼠追猫" 在它看来可能是一样的,这显然是不可接受的。
因此,必须引入一种信息来告诉模型每个词在序列中的位置,这就是位置编码(Positional Encoding, PE)的由来。
阶段一:绝对位置编码 (Absolute Positional Encoding)
最直接的想法是:为每个绝对位置(第0个、第1个、第2个...)赋予一个独特的编码。
正弦/余弦位置编码 (Sinusoidal PE)
出处:最早由 Transformer 论文《Attention Is All You Need》(2017) 提出。
思想:使用不同频率的正弦和余弦函数来为每个位置生成一个独特的向量。其公式为:
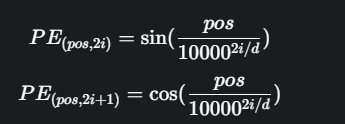
其中 pos 是位置,i 是向量的维度索引,d 是向量总维度。
优点:无需训练,是固定的;理论上可以外推到比训练时更长的序列。
缺点:它是通过加法(X_final = X_embedding + PE)注入位置信息的,这种方式不够“有机”,并且在深层网络中位置信息可能会被“冲淡”。
可学习的绝对位置编码 (Learned Absolute PE)
出处:由 BERT、GPT 等模型广泛采用。
思想:像词嵌入一样,创建一个位置嵌入矩阵 nn.Embedding(max_position, hidden_size)。每个位置(0, 1, 2...)对应一个可学习的向量,让模型在训练中自己学会每个位置的最佳表示。
优点:简单、直观、有效。
缺点:外推性极差。如果模型训练时最大长度是512,那么它完全不知道位置513应该是什么样的编码,泛化能力受限。
阶段二:相对位置编码 (Relative Positional Encoding)
研究者们很快意识到,单词的相对位置(比如两个词之间隔了多远)可能比它们的绝对位置更重要。
出处:Transformer-XL (2019) 等工作。
思想:不再将位置编码加到输入上,而是在计算注意力分数时引入一个表示相对距离的偏置项(bias)。计算 query_i 和 key_j 的注意力分数时,会额外加上一个代表 i 和 j 之间距离的学到的标量。
优点:直接建模相对位置,逻辑上更合理,泛化性更好。
缺点:实现更复杂,需要修改注意力计算的核心逻辑。
阶段三:旋转位置编码 (Rotary Positional Embedding, RoPE)
RoPE 是一种革命性的设计,它优雅地统一了绝对位置和相对位置的概念。
出处:论文《RoFormer: Enhanced Transformer with Rotary Position Embedding》(2021)。
核心思想:通过绝对位置来表达相对位置。它不把位置信息“加”到向量中,而是根据词的绝对位置,对 query 和 key 向量进行旋转。
想象一下,每个词的 query 和 key 向量都在一个二维复平面上。当一个词位于位置 m,就将它的 q 和 k 向量顺时针旋转 m * θ 度。当计算位置 m 的 query 和位置 n 的 key 的注意力(点积)时,它们的夹角只取决于 (m-n) * θ,也就是它们的相对位置 m-n,而与绝对位置 m 和 n 无关。
优点:
实现了相对位置编码:注意力分数仅依赖于相对位置。
外推性好:由于其周期性,可以很好地泛化到更长的文本。
无参数:像正弦编码一样,无需学习。
实现简洁:无需修改注意力评分的核心,只需在送入注意力计算前,对 Q 和 K 向量进行预处理即可。
正因为这些优点,RoPE 成为了 Llama、Qwen 等现代主流大模型的首选。
第二部分:Qwen3 RoPE 代码深度解析
def apply_rotary_emb(
x: torch.Tensor,
cos: torch.Tensor,
sin: torch.Tensor,
) -> torch.Tensor:
# cos 和 sin 的形状是 (num_tokens, rotary_dim/2)
# 增加一个维度以进行广播,形状变为 (num_tokens, 1, rotary_dim/2)
cos = cos.unsqueeze(-2)
sin = sin.unsqueeze(-2)
# 将输入的向量 x (query 或 key) 在最后一个维度上切成两半
# x1 和 x2 的形状都是 (num_tokens, num_heads, rotary_dim/2)
x1, x2 = torch.chunk(x.to(torch.float32), 2, dim=-1)
# 这两行就是 RoPE 的核心数学操作,等同于一个二维旋转矩阵的乘法
# 对应于复数乘法 z * e^(iθ) = (x1+ix2)(cosθ+isinθ) 的实部和虚部
y1 = x1 * cos - x2 * sin
y2 = x2 * cos + x1 * sin
# 将旋转后的两半重新拼接起来
return torch.cat((y1, y2), dim=-1).to(x.dtype)
这部分代码实现的是 d/2 个二维旋转。x 向量的 head_size 维度被两两一组,看作是 head_size/2 个二维向量 [x_i, x_{i+1}]。每个二维向量都乘以一个由 cos 和 sin 构成的旋转矩阵:
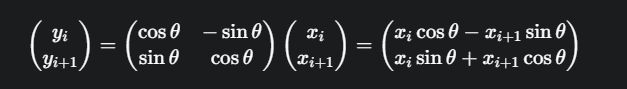
RotaryEmbedding 类 - 预计算与应用
class RotaryEmbedding(nn.Module):
def __init__(...):
super().__init__()
# ... 初始化参数 ...
# --- 预计算 cos 和 sin 缓存 ---
# 1. 计算旋转频率 theta
# inv_freq 的形状是 (rotary_dim/2),包含了 d/2 个不同的频率
inv_freq = 1.0 / (base**(torch.arange(0, self.rotary_dim, 2, dtype=torch.float) / self.rotary_dim))
# 2. 创建所有可能的位置索引
# t 的形状是 (max_position_embeddings)
t = torch.arange(self.max_position_embeddings, dtype=torch.float)
# 3. 计算每个位置(t)在每个频率(inv_freq)上的旋转角度
# einsum("i,j -> ij") 是计算外积的优雅方式,结果 freqs[i, j] = t[i] * inv_freq[j]
# freqs 的形状是 (max_position_embeddings, rotary_dim/2)
freqs = torch.einsum("i,j -> ij", t, inv_freq)
# 4. 计算所有角度的 cos 和 sin 值
cos = freqs.cos()
sin = freqs.sin()
# 5. 将 cos 和 sin 拼接在一起,方便一次性查找
cache = torch.cat((cos, sin), dim=-1)
# 6. 注册为 buffer
# register_buffer 意味着它是模型状态的一部分,会随模型移动(如.to(device))
# 但它不是模型参数,不会在训练中被优化器更新
self.register_buffer("cos_sin_cache", cache, persistent=False)
@torch.compile # PyTorch 2.0 的 JIT 编译器,用于加速
def forward(...):
# ...
# 从缓存中根据当前批次中所有 token 的位置 `positions`,高效地取出对应的 cos 和 sin 值
cos_sin = self.cos_sin_cache[positions]
cos, sin = cos_sin.chunk(2, dim=-1)
# ... Reshape Q 和 K, 应用旋转 ...
query = apply_rotary_emb(query, cos, sin).view(query_shape)
key = apply_rotary_emb(key, cos, sin).view(key_shape)
return query, key
解读:
缓存思想:在模型初始化时,一次性计算出所有可能位置(最多 max_position_embeddings 个)的旋转参数并存起来。在实际计算时,只需根据 positions 列表进行查表操作,速度极快。
@torch.compile:这是一个优化器装饰器,可以将这部分热点代码编译成更高效的底层代码,进一步加速计算。
@lru_cache(1)
def get_rope(...):
assert rope_scaling is None # 当前实现不支持 rope_scaling
rotary_emb = RotaryEmbedding(head_size, rotary_dim, max_position, base)
return rotary_emb
解读:
@lru_cache(1):这是 Python 内置的一个装饰器,用于缓存函数调用结果(LRU = Least Recently Used)。
作用:在一个复杂的模型中,可能会有多处代码需要获取 RoPE 实例。@lru_cache(1) 保证了对于同样一套参数(head_size, max_position 等),RotaryEmbedding 这个昂贵的对象只会被创建一次。后续所有调用都会立即返回第一次创建的那个缓存好的实例,避免了重复的计算和内存分配,是一种非常好的工程实践。
总结
这份 Qwen3 的 RoPE 实现是高效、简洁且工程化的典范:
数学上正确:apply_rotary_emb 精准实现了 RoPE 的核心旋转操作。
计算上高效:通过在 init 中预计算和缓存 cos_sin_cache,将前向传播中的昂贵计算转变为快速的查表操作。
工程上健壮:使用 @lru_cache 确保 RoPE 实例在整个模型中是单例的,节省了资源。同时使用 @torch.compile 进一步 JIT 加速热点代码。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号