机器学习-线性分类-支持向量机SVM-SMO算法-14
1. SVM算法总结
-
选择 核函数 以及对应的 超参数
为什么要选择核函数?
升维 将线性问题不可分问题 升维后转化成 线性可分的问题
核函数 有那些? linea gauss polinormail tanh -
选择惩罚项系数C
min ||w||2 + Csum(ei) -
构造优化问题:
![]()
-
利用SMO算法 计算 α*
-
根据α* 计算w*
-
根据α* 得到支撑向量 计算每个支撑向量 对应的bs*
-
bs* 求平均得到b*
学得超平面:![]()
仔细观察这个式子就会发现:
其实只需要关注 支撑向量的C>α>0 非支撑向量的alpha为0
W*的计算:
![]()
其实也就只需要关注 是支撑向量的几个点,支撑向量对于W,b的求解起关键作用,其他的非支撑向量,对模型没起任何作用
- 得到最终的判别式
![]()
神奇的SMO算法到底是如何进行的?
2. SMO算法
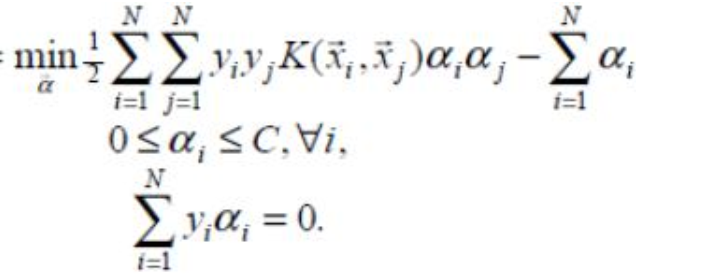
其中(xi,yi)表示训练样本数据,xi 为样本特征,yi∈{−1,1}为样本标签,C 为惩罚系数由自己设定。上述问题是要求解 N 个参数(α1,α2,α3,...,αN),其他参数均为已知
把原始求解 N 个参数二次规划问题分解成很多个子二次规划问题分别求解,每个子问题只需要求解 2 个参数,方法类似于坐标上升,节省时间成本和降低了内存需求。每次启发式选择两个变量进行优化,不断循环,直到达到函数最优值。
同时优化两个参数,固定其他 N-2 个参数,假设选择的变量为α1,α2,
固定其他参数α3,α4,...,αN,由于参数α3,α4,...,αN 的固定, 可以简化目标函数为只关于α1,α2的二元函数,Constant 表示常数项(不包含变量α1,α2 的项)。
v1 表示 x1 与 3---N 之后所有的样本运算
v2 表示 x2 与 3---N 之后所有的样本运算
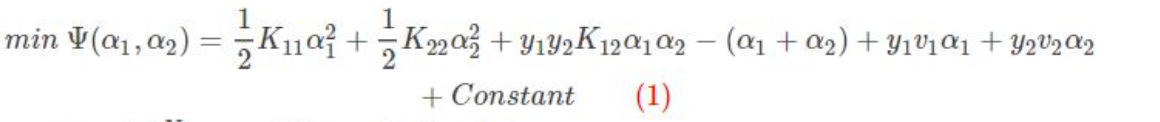
其中:

Kij表示 xi 与 xj 输入到核函数 进行运算的结果
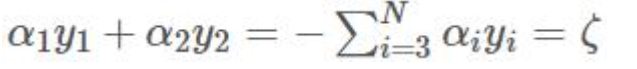
两边同时乘以 y1, 任意的y*2 = 1
得到:
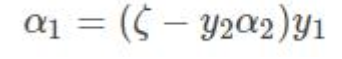
需要优化的目标函数转化成:

上式中是关于变量α2 的函数,对上式求导并令其为 0 得:
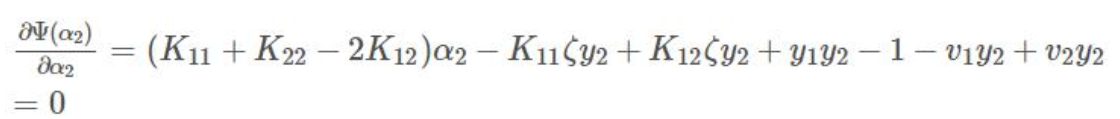

将4, 6, 7 带入求导=0 的式子
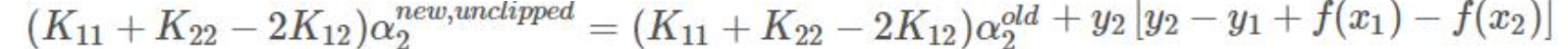
令η=K11+K22−2K12
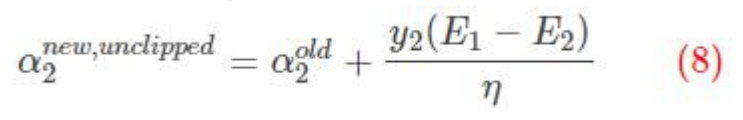
这里得到的α2 是未经过修建的alpha 不一定满足约束条件
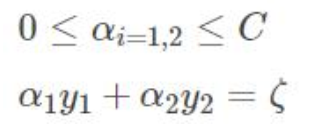


翻译一下:
两个拉格朗日算子 0< α1 α2 < C限定必须在正方形盒子内部
α1y1+α2y2=固定值 限定了必须在直线上 最优解 必须是一条线段
新的α2 下限L 上限H

修建后的alpha
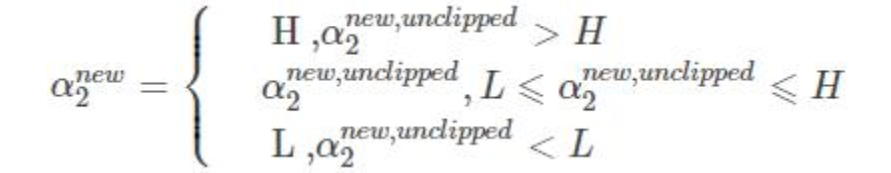
由于其他 N-2 个变量固定:

两边同时乘以y1:
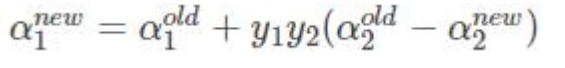
选择α1 α2采用上述方法进行优化,直到不违反kkt条件

α1 α2优化的同时对b进行更新:
- 如果:
![]()
则 x1 y1 为支撑向量![]()
两边乘以y1:
![]()
得到bnew:
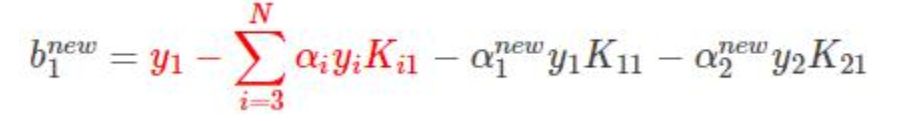
只不过是拆成3部分而已
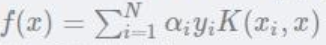

前两项可以替换为
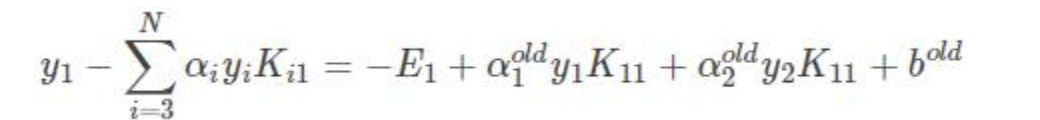
得到:
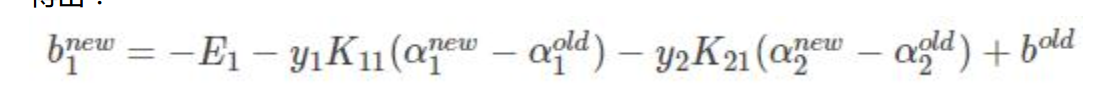
如果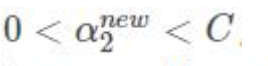
同理:
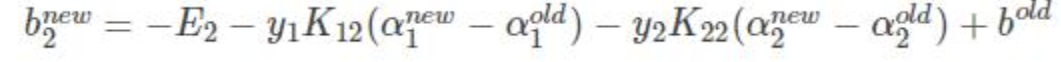
-
α1 α2 都满足:
![]()
取一个就行:![]()
-
如果都不满足 他们的中点:
取1/2 *(α1 + α2)

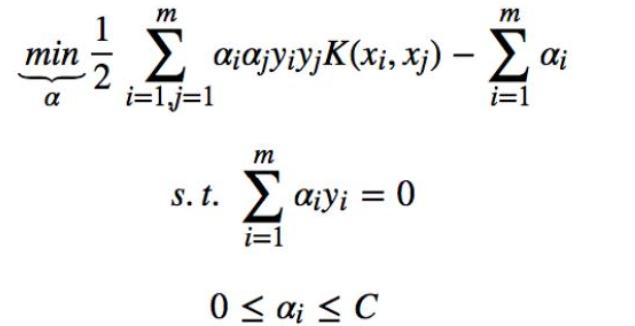
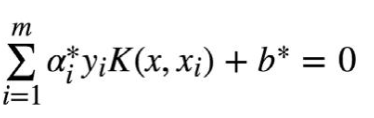
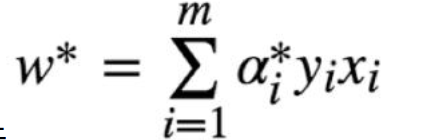

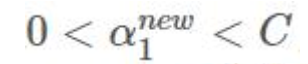

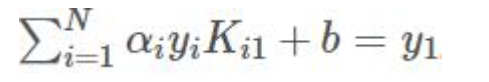
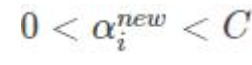
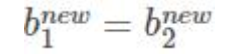

 浙公网安备 33010602011771号
浙公网安备 33010602011771号