数学基础-快速幂、快速乘、矩阵快速幂

快速幂

幂运算的本质是做乘法，对于 \(a^b\)，其核心思想是将指数 \(b\) 进行二进制分解，然后对 \(b\) 的每一位进行进行乘法，时间复杂度为 \(O(\log b)\)。

ll quick_power(ll a, ll b, ll p) {
    ll ans = 1 % p;
    for (; b; b >>= 1) {
        if (b & 1)
            ans = ans * a % p;
        a = a * a % p;
    }
    return ans;
}

快速乘

乘法运算的本质是做加法，对于 \(a\times b\)，其核心思想是将乘数 \(b\) 进行二进制分解，然后对 \(b\) 的每一位进行进行加法，\(O(\log b)\)。

ll quick_power(ll a, ll b, ll p) {
    ll ans = 0;
    for (; b; b >>= 1) {
        if (b & 1)
            ans = (ans + a) % p;
        a = a * 2 % p;
    }
    return ans;
}

矩阵快速幂

定义矩阵类，重载乘法运算符*，方便后续使用：

template <class T>
class Matrix {
public:
    int n, m;
    vector<vector<T>> mat;
    Matrix(int _n) : n(_n), m(_n) {
        mat = vector<vector<T>>(n, vector<T>(m));
    }

    Matrix(int _n, int _m) : n(_n), m(_m) {
        mat = vector<vector<T>>(n, vector<T>(m));
    }

    Matrix operator*(const Matrix &b) const {
        assert(m == b.n);
        Matrix c = Matrix(n, b.m);
        for (int i = 0; i < c.n; i++) {
            for (int j = 0; j < c.m; j++) {
                for (int k = 0; k < m; k++) {
                    c.mat[i][j] = (c.mat[i][j] + mat[i][k] * b.mat[k][j]) % mod;
                }
            }
        }
        return c;
    }

    void Input() {
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                cin >> mat[i][j];
            }
        }
    }

    void Output() {
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                cout << mat[i][j] << " \n"[j == m - 1];
            }
        }
    }

    Matrix I(int _n) {
        Matrix I = Matrix(_n);
        for (int i = 0; i < _n; i++) {
            I.mat[i][i] = 1;
        }
        return I;
    }
};

定义矩阵快速幂：

Matrix<int> matrix_power(Matrix<int> a, ll b) {
    Matrix<int> ans = a.I(a.n);

    for (; b; b >>= 1) {
        if (b & 1)
            ans = ans * a;
        a = a * a;
    }
    return ans;
}

1.矩阵快速幂可用于解决递推次数很大的问题，例如递推次数为 \(10^{18}\)。
此类问题的核心是确定要求的第 \(n\) 项 \(F(n)\) 需要用哪些变量，通过哪些常系数组合表示。

例题：
又见斐波那契
题目描述
给定递推式：

\[F(x)= \begin{cases} F(i-1) + F(i-2) + i^3 + i^2 + i + 1& i>1\\ 0& i=0\\ 1& i=1 \end{cases} \]

求 \(F(n)\) 的值，由于这个值可能太大，请对 \(10^9+7\) 取模。

输入描述
第一行是一个整数 \(T(1\le T\le 1000)\)，表示样例的个数。
以后每个样例一行，是一个整数 \(n(1\le n\le 10^{18})\)。

输出描述
每个样例输出一行，一个整数，表示 \(F(n)\mod10^9+7\)。

问题分析

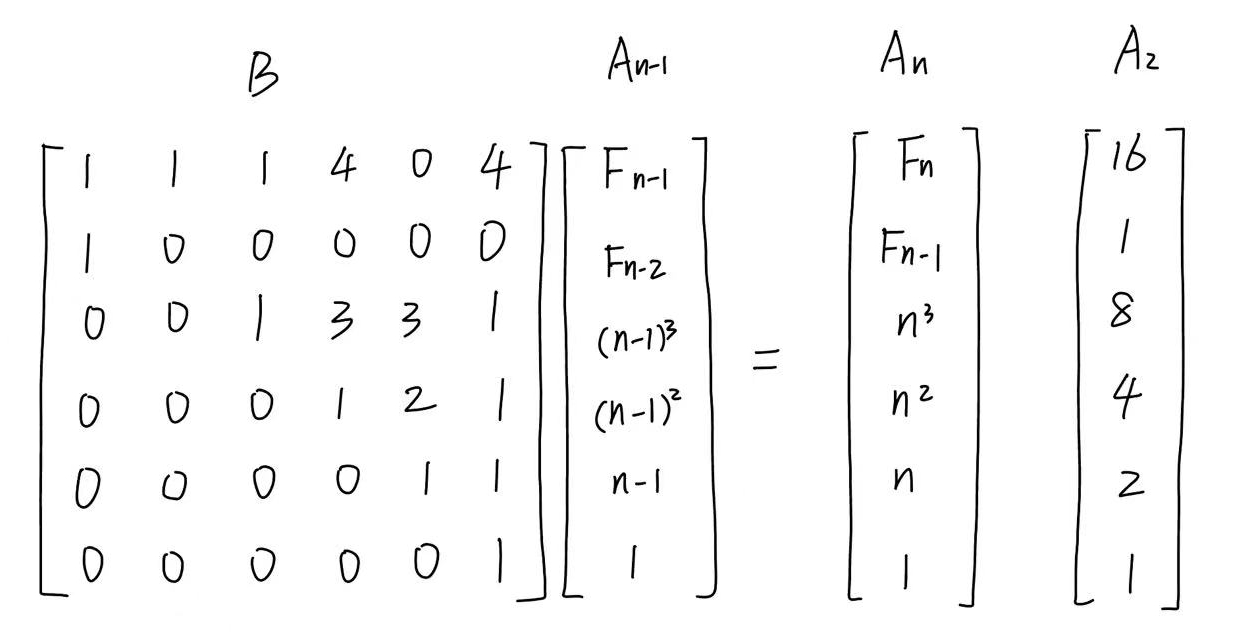
首先 \(A_n\) 的第一个元素为所求的 \(F_n\)，根据 \(A_n\) 确定 \(A_{n-1}\) 中需要哪些元素，然后确定 \(B\) 中的系数，最后确定 \(A_n\) 的初值，本题中从 \(A_2\) 开始。

核心代码

void solve() {
    int n;
    cin >> n;
    if (n < 2) {
        cout << n << "\n";
    } else {
        Matrix<int> A(6, 1), B(6, 6), ans(6, 1);
        A.mat = vector<vector<int>>({{16}, {1}, {8}, {4}, {2}, {1}});
        B.mat = vector<vector<int>>({{1, 1, 1, 4, 6, 4},
                                     {1, 0, 0, 0, 0, 0},
                                     {0, 0, 1, 3, 3, 1},
                                     {0, 0, 0, 1, 2, 1},
                                     {0, 0, 0, 0, 1, 1},
                                     {0, 0, 0, 0, 0, 1}});
        ans = matrix_power(B, n - 2) * A;
        cout << ans.mat[0][0] << "\n";
    }
}

2.矩阵快速幂还可用于解决图论中根据邻接矩阵求路径长度的问题。
由于邻接矩阵 \(A\) 的 \(m\) 次幂中的每一个元素 \(A^m_{i,j}\) 即为图中从 \(i\) 到 \(j\) 长度为 \(m\) 的路径条数，故求图中路径长度为 \(m\) 的路径条数即对 \(A^m\) 中的每一个元素求和。

例题：
Walk
核心代码

    int n, m;
    cin >> n >> m;
    Matrix<int> A(n);
    A.Input();
    A = matrix_power(A, m);

    int ans = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            ans = (ans + A.mat[i][j]) % mod;
        }
    }
    cout << ans << "\n";
}

矩阵快速幂的时间复杂度为 \(O(m^3\log n)\)，其中 \(m\) 为矩阵规模，\(n\) 为指数。