离散实验1：可简单图化、 连通图和欧拉图的判断

实验题目：

可简单图化、 连通图和欧拉图的判断。

实验要求：

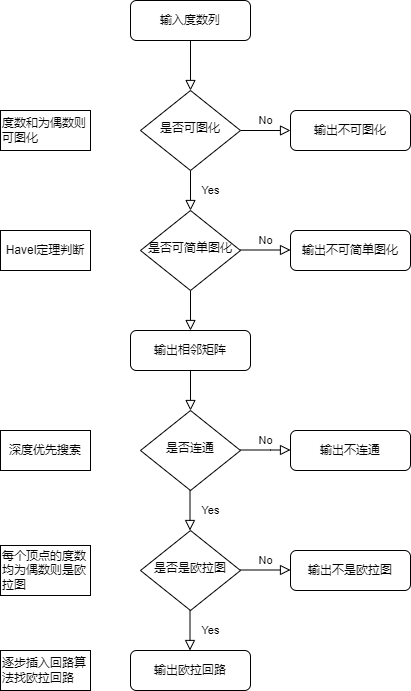
1. 给定一非负整数序列（例如： (4,2,2,2,2)）。
2. 判断此非负整数序列是否是可图化的，是否是可简单图化的。
3. 如果是可简单图化的，根据 Havel 定理过程求出对应的简单图，并输出此简单图的相邻矩阵（默认第 i 行对应顶点 vi）。
4. 判断此简单图是否是连通的。
5. 如果是连通图，判断此图是否是欧拉图。如果是欧拉图，请输出一条欧拉回路（输出形式如： v2->v1->v5->v3->v4->v5->v2）。
   说明： 要求学生设计的程序不仅对给定非负整数序列得出正确结果，还要对教师测试数据集得出正确结果，编程语言不限。

流程图：

源代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>
#include<ctime>
#include<stack>
using namespace std;
 
const int N = 100;//最大度数列
int martix[N][N];//图的相邻矩阵
bool visit[N];//dfs用来判断是否经过
bool visit2[N][N];//Fleury算法用来判断是否经过
int len = 1;//度数列长度
int m = 0;//边数
int cnt = 0;//计数判断连通图
pair<int, int>v[N];//v[i].first放度数列，v[i].second放点序号
bool issimple = true;//判断是否是简单图
bool iseuler = true;//判断是否是欧拉图
bool isnegative = false;//判断是否是负数
stack<int> s;//逐步插入回路算法储存顶点
 
/*Havel定理判断是否可简单图化，若可简单图化，建立图的邻接矩阵*/
bool Havel() {
	for (int j = 0; j < len; j++) {
		sort(v, v + len, greater<pair<int, int>>());
		if (v[0].first == 0) {//如果第一个数是0
			return true;
		}
		for (int i = 0; i < v[0].first; i++) {
			v[i + 1].first--;
			//建立图的相邻矩阵
			martix[v[0].second][v[i + 1].second] = martix[v[i + 1].second][v[0].second] = 1;
			m++;//边数加一
			if (v[i + 1].first < 0) {
				return false;
			}
		}
		v[0].first = 0;
	}
	return false;
}
 
/*深度优先搜索*/
void dfs(int x) {
	visit[x] = true;
	cnt++;
	for (int i = 0; i < len; i++) {
		if (martix[x][i] && !visit[i]) {
			dfs(i);
		}
	}
}
 
/*dfs判断是否连通，若cnt = len，则连通*/
bool Connect() {
	for (int i = 0; i < len; i++) {
		cnt = 0;
		dfs(i);
		if (cnt == len) {
			return true;
		}
	}
	return false;
}
 
/*逐步插入回路算法（又称Hierholzer算法）找欧拉回路*/
void Hierholzer(int k) {
	for (int i = 0; i < len; i++) {
		if (martix[k][i] && !visit2[k][i]) {
			visit2[k][i] = 1;
			visit2[i][k] = 1;
			Hierholzer(i);
		}
	}
	s.push(k);//栈用于储存顶点
}
 
int main() {
	while (1) {
		cout << "请输入非负整数列元素个数(输入0结束程序)：" << endl;
		cin >> len;
		if (len <= 0) {
			break;
		}
		int sum = 0;
		m = 0;
		cnt = 0;
		iseuler = true;
		issimple = true;
		memset(v, 0, sizeof(v));
		memset(martix, 0, sizeof(martix));
		memset(visit, 0, sizeof(visit));
		memset(visit2, 0, sizeof(visit2));
		while(!s.empty()) {
			s.pop();
		}
		cout << "请输入度数列(中间用空格隔开)：" << endl;
		for (int i = 0; i < len; i++) {
			int di;
			cin >> di;
			if (di < 0) {
				isnegative = true;
			}
			if (di % 2) {
				iseuler = false;
			}
			v[i].first = di;
			v[i].second = i;
			sum += di;
		}
		if (isnegative) {
			cout << "输入错误，度数列必须为非负整数！" << endl;
			break;
		}
		else if (sum % 2) {
			cout << "不可图化" << endl;
		} else {
			cout << "可图化" << endl;
			if (Havel()) {
				cout << "可简单图化" << endl << "图的相邻矩阵：" << endl;
				printf("    ");
				for (int i = 1; i <= len; i++) {
					printf("V%d ", i);
				}
				cout << endl;
				for (int i = 1; i <= len; i++) {
					printf("V%d ", i);
					for (int j = 0; j < len; j++) {
						printf(" %d ", martix[i - 1][j]);
					}
					cout << endl;
				}
				if (Connect()) {
					cout << "连通图" << endl;
					if (iseuler) {
						cout << "欧拉图" << endl;
						cout << "其中一条欧拉回路为：" << endl;
						srand((unsigned)time(NULL));
						unsigned long long start = clock();
						Hierholzer(0);
						while(!s.empty()) {
							cout << "V" << s.top() + 1;
							s.pop();
							if(!s.empty()) {
								cout << "->";
							}
						}
						cout << endl << "计算用时：" << (clock() - start) / 1000.0 << "s" << endl;
					} else {
						cout << "非欧拉图" << endl;
					}
				} else {
					cout << "非连通图" << endl;
				}
			} else {
				cout << "不可简单图化" << endl;
			}
		}
		cout << endl;
	}
	return 0;
}