大模型损失函数（一）：交叉熵、联合熵、条件熵

1. 信息熵

在信息论中，熵衡量概率分布中的不确定性。

 

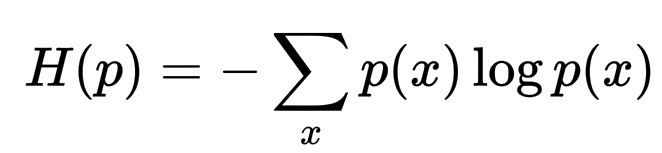
H(p) = -\sum_x p(x) \log p(x)

如果 p(x) 出现一个尖峰，一种结果几乎是确定的，则熵较低。如果 p(x) 分布广泛，多种结果皆有可能，则熵较高。从这个意义上讲，熵是一个系统的平均意外（混乱程度）。

2. 语言模型中的损失函数——交叉熵（cross entropy）

当模型学习预测下一个标记 x 时，模型会生成一个分布 q(x)。在训练过程中，损失函数会将预测分布 q(x) 与真实分布 p(x) 进行比较，最小化的损失函数是它们之间的交叉熵：

 

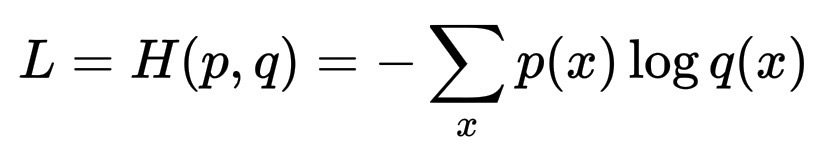
L = H(p, q) = -\sum_x p(x)\log q(x)

其中：

- p(x) = 每个结果的真实概率（来自数据）。
- q(x) = 模型的预测概率。

所以 H(p, q) 不关心两个随机变量的关系；它关心的是一个随机变量 X，其真实分布为 p，而另一个系统（模型）赋予它的概率为 q。它衡量的是，如果世界真的遵循 p，模型 q 平均会有多意外。

模型如何“降低熵”？我们可以用一种更直观的方式重写这个损失函数：

H(p, q) = H(p) + D_{KL}(p ∥ q)

这里，D_{KL}（Kullback-Leibler 散度）衡量了预测的世界与真实世界之间的距离。

- H(p) 是固定的，它是数据（上下文）本身的熵。
- D_{KL}(p ∥ q) 模型实际可以减少的。

所以，当模型训练时，模型不仅仅是在记忆，模型还在减少内部分布与现实之间的差异，这反过来又降低了预期意外。

---

联合熵（joint entropy） H(X, Y)，这是完全不同的概念：

 

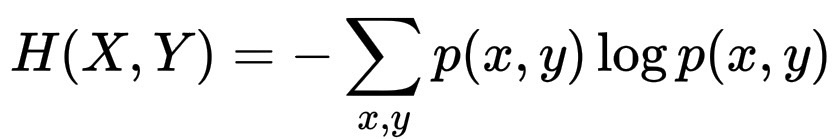
H(X, Y) = -\sum_{x,y} p(x, y)\log p(x, y)

这里我们处理的是两个随机变量 X 和 Y，它们的联合分布为 p(x, y)。它衡量的是这两个变量合在一起的总不确定性，平均需要多少比特才能同时描述 X 和 Y。

交叉熵和联合熵具有相同的数学形式，概率乘以对数之和，但代表不同的关系：一个是同一变量的两个分布之间的关系，另一个是同一分布下的两个变量之间的关系。

---

条件熵（conditional entropy）作为“剩余不确定性”：如果你已经知道 Y，那么你对 X 的不确定性程度如何？这就是条件熵：

 

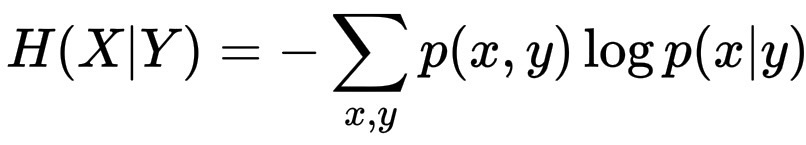
H(X|Y) = -\sum_{x,y}p(x,y)\log p(x|y)

它衡量的是 Y 被揭示后 X 中剩余的平均不确定性。

它和联合熵的关键关系如下：H(X,Y) = H(Y) + H(X|Y)。或者等价地，H(X|Y) = H(X,Y) - H(Y)

因此，联合熵自然分解为，H(Y)：Y 本身的不确定性，和，H(X|Y)：在知道 Y 之后，X 剩下的部分。

回到交叉熵，交叉熵 H(p,q) 可以看作是条件熵的推广：它是将真实的条件熵 p(x|y) 替换为模型的近似值 q(x|y) 时的结果，这就是为什么训练模型就像是最小化它在真实条件结构之外添加的“额外不确定性”。

---

因此，交叉熵不会忽略 y，它假设 y 是已经给定的、固定的，这个条件定义了上下文。

正式地说，我们可以将语言模型的交叉熵版本写为：

 

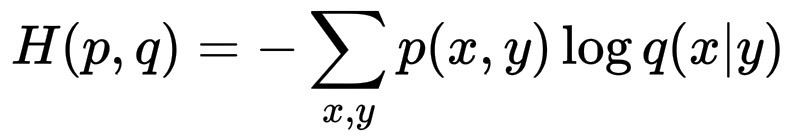
H(p,q)= -\sum_{x,y}p(x,y)\log q(x|y) 

这里将 y 视为上下文（已经出现过的单词），将 x 视为下一个标记。一旦 y 已知，剩下的不确定因素就是 x，不同的系统 q 会产生不同的条件分布 q(x|y)。

所以，y 在那一刻是不可变的，它是我们设定条件的信息。交叉熵随后比较每个系统的条件世界 q(x|y）与真实条件世界 p(x|y) 的偏离程度。差异越小，系统在相同条件下反映现实的准确性就越高。