大模型推理（八）：舍入误差 rounding error

 “舍入误差”（rounding error），最简单的理解是，当连续的数学量以离散的数值格式表示时，就会发生舍入误差，比如计算机中的浮点数。并非所有实数都能精确存储，因此机器会保留一个近似值。

形式上，如果真值为 x，存储值为 \hat{x}，则

\hat{x} = x + \epsilon

其中 \epsilon 是舍入误差，通常与机器精度一致（例如，对于 64 位浮点数，约为 10^{-16}）。

在大型语言模型内部，模型并不直接用“单词”来思考，而是将它们表示为向量，一个捕捉其在高维空间中含义的数字列表。因此，当模型计算类似下一个单词的概率分布时：

 

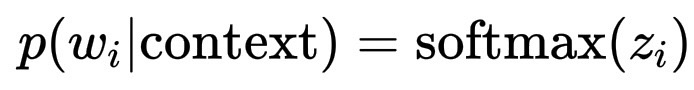
p(w_i | \text{context}) = \text{softmax}(z_i)

其中 z_i 是 logits（非归一化分数），大型浮点向量。

每个 z_i 值、网络中的每个权重、训练期间的每个梯度，它们都是浮点近似值。某一层的微小舍入误差可能会稍微改变下一个激活的神经元，从而将概率从 0.300001 微调到 0.299999。

通常这无关紧要，但在漫长而细致的对话中，这种微小的变化可能会在网络中产生连锁反应，微妙地改变语气、措辞或词汇选择。

---

有限精度的概念。在计算机中，每个实数都必须用有限位数存储。假设系统只能保留t位有效数字，任何实数 x 都会被舍入到接近 \hat{x} 的值：\hat{x} = x + \epsilon

舍入误差为：\epsilon = \hat{x} - x

我们通常将其描述为相对误差：

 

\frac{|\epsilon|}{|x|} \leq \text{machine epsilon} = \varepsilon_{\text{mach}}

对于双精度（大多数系统使用的格式）：

 

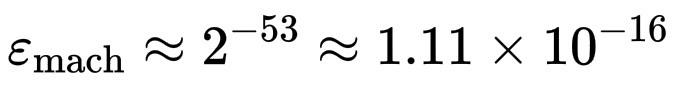
\varepsilon_{\text{mach}} \approx 2^{-53} \approx 1.11 \times 10^{-16}。

误差为何重要？每次计算（加法、乘法、幂运算）时，都会有一个微小的舍入误差进入结果。如果重复多次操作（就像神经网络数十亿次那样），这些误差可能会累积或略微放大。

例如，假设我们要将一个非常小的数加到一个很大的数上：x = 10^{10}, y = 10^{-5}

在实际算术中：x + y = 10^{10} + 10^{-5}

但在有限机器上，10^{10} 和 10^{10} + 10^{-5} 的存储位相同，小数太小，无法改变存储的值。因此，和就是 10^{10}。这就是舍入误差的一种：显著性损失。

这在大模型中会产生连锁效应，现在想象一下数百万次矩阵乘法，每个 W_l、h_l、b_l 都带有微小的舍入差异。在数千层中，这些微小的 ε 会微妙地改变最后的 softmax 概率。虽然不足以改变含义，但足以使短语听起来不同。常见的一个问题是语序颠倒，这在描述性场景问题不大，但是对于严格的数学定义或是代码，就会产生明显的错误。