二阶方向导数：凸函数来到高维空间

想象一根碗里的筷子，两端搁在表面上，但中间浮在上面，这时的碗就是一个凸面。

好的，现在的问题是：二阶导数检验的高维版本是什么？

在一维中，f''(x) > 0 告诉我们凸性。但现在我们有一个包含两个变量的函数 f(x,y)。我们可以求偏导数，x 方向的变化率和 y 方向的变化率。

我们也可以求二阶偏导数。有∂²f/∂x²、∂²f/∂y²，以及混合偏导数，例如∂²f/∂x∂y。所有这些二阶导数都被组织成一个矩阵，一个由数字组成的方格。而“那个”矩阵……就是 Hessian 矩阵！

 

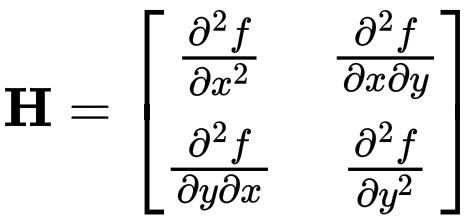
\mathbf{H} = 
\begin{bmatrix}
\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2} \\
\end{bmatrix}

所以我们已经到了！Hessian 矩阵只是“二阶导数”在多维空间的自然推广。就像f''(x)告诉你一维空​​间的曲率一样，Hessian 矩阵告诉你高维空间的“曲率”。

---

我们为什么需要这些奇怪的混合导数？

首先是好消息：∂²f/∂x∂y 和 ∂²f/∂y∂x 实际上是同一个东西（对于光滑的函数来说）。顺序无关紧要，但真正的问题是：我们为什么需要它们？

这样想，∂²f/∂x² 告诉你曲面在纯 x 方向上的弯曲程度，就像你沿着与 x 轴平行的方向切开一个碗一样。 ∂²f/∂y² 表示纯 y 方向的曲率。但是……对角线方向呢？如果你沿着曲面东北方向行走，或者沿着任何其他对角线路径行走，会怎么样？

混合导数 ∂²f/∂x∂y 捕捉的是曲面的扭曲。它测量的是 x 轴的增加是否会改变曲面在 y 方向上的陡度。

想象一个马鞍形曲面，它在一个方向上向上弯曲，在另一个方向上向下弯曲。纯二阶导数可能无法捕捉到这种扭曲。但混合导数可以。

---

假设你沿着 x = y 轴行走，也就是说你在 x 和 y 方向上的移动量相等。如果表面在 x 方向上向上弯曲，在 y 方向上向下弯曲的量相同，那么直觉上，是的，它们可能会抵消，你甚至会沿着某个平面行走！

“马鞍面”并非指某种特定的形状，它涵盖了一系列曲面。它们都具有朝一个方向向上弯曲、朝另一个方向向下弯曲的特性，但细节取决于具体的函数。

例如：

- f(x,y) = x² - y² 是马鞍面
- f(x,y) = xy 也是马鞍面
- f(x,y) = x² - 2y² 也是马鞍面

它们都是马鞍面，但扭曲方式不同！混合导数 ∂²f/∂x∂y 各不相同。

所以，当你沿着 x = y 的对角线行走时，你的体验，无论是平地、上坡、下坡，还是坡度，都取决于具体的公式。Hessian 矩阵捕捉到了所有这些信息：x 方向的曲率、y 方向的曲率，以及扭曲度。这就是 Hessian 矩阵如此强大的原因，它不仅仅告诉你“这是一个马鞍形”或“这是一个碗状”。它准确地告诉你表面是如何在各个方向上弯曲和扭曲的。

---

 “v 方向曲率”有两种截然不同的含义，根据你具体想问什么，测量“曲率”的方法有很多种。

公式 v^T H v 为二阶方向导数（second directional derivative）。它告诉你当你沿着方向 v 行走时，斜率的变化速度，这是曲率的一个概念。其中，f 为 v 方向的“二阶方向导数” 高度函数，f(x,y) 在 xy 平面上沿 v 弯曲的速度（纯解析），v 通常在 \mathbb{R}^2 中被视为单位向量：

 

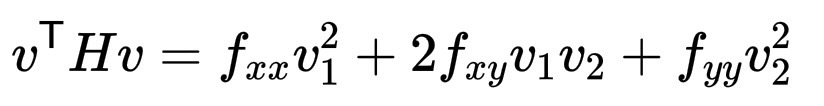
v^\mathsf{T} H v = f_{xx}v_1^2 + 2f_{xy}v_1v_2 + f_{yy}v_2^2 

但是，如果你从微分几何的角度来查找“曲率”，比如嵌入空间的曲线的曲率，你可能会发现分子是 v^T H v，分母是某种归一化函数。例如，如果曲面以图形 z = f(x, y)  的形式给出，并且你正在寻找由水平单位向量 (v_1, v_2)  给出的方向上的法向曲率（normal curvature），则公式（从一般公式推导而来）简化为：

 

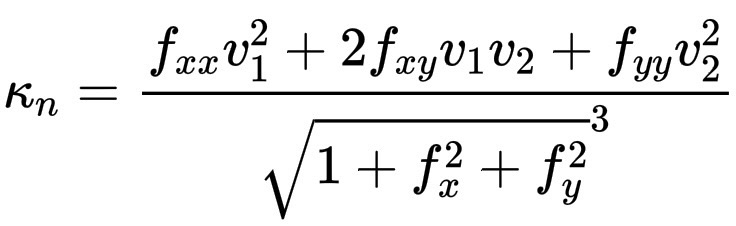
\kappa_n = \frac{f_{xx}v_1^2 + 2f_{xy}v_1v_2 + f_{yy}v_2^2 }{\sqrt{1 + f_x^2 + f_y^2}^3}