柯尔莫哥洛夫复杂度与停机问题

想象一下，你有一个信息，比如一串数字、一张图片或一段旋律。现在来问自己：“能够生成这个信息的最短计算机程序是什么？”这个最短程序的长度，以比特为单位，就是该对象的柯尔莫哥洛夫复杂度（Kolmogorov complexity）。

这不再是关于概率的问题；而是关于描述的问题，重现这个对象需要多少理解？

形式上，字符串 x 相对于通用计算机 U 的柯尔莫哥洛夫复杂度为：

 

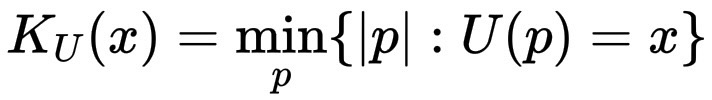
K_U(x) = \min_{p} \{ |p| : U(p) = x \}

其中，U 是某种通用图灵机，基本上是任何计算机的模型。p 是一个程序，一个比特序列。|p| 是该程序的比特长度。

因此，K_U(x) 是输出 x 且程序终止的最短程序的长度。如果不存在比直接打印数据更短的程序，那么 x 就是不可压缩的。或者，用诗意的语言来说，它是没有结构的纯粹信息。

为什么它很重要？如果 K(x) 很小，则对象具有结构，可以利用的模式、对称性、重复或逻辑，例如：“1010101010…” 可以描述为“重复 10 五次”。如果 K(x) 很大，则该对象没有更简单的解释，它本身就是随机的，例如：“1011010110…” 没有任何可发现的规则。从这个意义上讲，复杂度与随机性相反，或者更确切地说，当描述失效时，随机性就是复杂度的最大值。

你可以定义柯尔莫哥洛夫复杂度，但你实际上无法计算任意数据的复杂度。因为要知道一个程序是否是最短的，你必须解决停机问题，而停机问题是可证明不可判定的。

---

停机问题是什么？假设你有两个东西：一个程序 P，以及一个输入 x。

问题是，“你能否编写另一个程序 H(P, x)，使其能够正确判断 P 在输入 x 上运行时最终是会停止（结束），还是会永远运行下去？”

简单来说，一台计算机能否完美地预测任何其他计算机的行为，而无需实际运行它直至完成？

1936 年，艾伦·图灵证明了不存在这样的通用程序 H。为什么？因为如果 H 存在，就可以利用它制造逻辑悖论，自相矛盾。他设想了以下巧妙的设置：

假设 H(P, x) 存在。现在构建一个新的程序 D(Q)，该程序：

1. 使用 H 分析输入为 Q 的 Q。

2. 如果 H 的结论是“Q 终止”，则 D 将无限循环。

3. 如果 H 的结论是“Q 不终止”，则 D 终止。

现在，如果将 D 代入自身 D(D)，会发生什么？如果 H 的结论是 D 终止，则根据定义，D 将无限循环。如果 H 的结论是 D 循环，则 D 将终止。这个矛盾表明 H 不存在。因此，没有一种通用的方法可以预先判断任意程序是否会终止。

---

假设我们正在寻找能够输出特定对象，例如，一串数字、一张图片或一段旋律的最短程序。我们可以想象逐一测试所有可能的程序。有些程序会很快停止并产生结果，而另一些程序似乎会永远运行下去。

问题是，我们如何知道一个运行了很长时间的程序永远不会停止？也许它会在运行一百万年后停止，或者也许它会无限循环。除了让它永远运行下去之外，没有通用的方法来判断，而我们当然不可能做到这一点。

要知道真正的柯尔莫哥洛夫复杂度 K(x)，我们需要验证是否存在更短的程序能够生成 x。但如果我们无法判断这些更短的程序是否会终止，我们就无法确定它们最终不会生成 x。

因此，我们永远无法证明我们已经找到了绝对的最小长度描述。我们只能通过压缩、启发式或洞察力来近似它，但理论上的理想状态总是与我们擦肩而过。