有一种考前背书的美（省选 2026 Edition）

考前复习资料（省选 2025 Edition）

有一些太熟悉的例如线段树、树状数组、FWT 感觉就不写了。注意，要看的是不熟悉的！

目录

经典永流传

OI 赛制比赛 emergency kit（2024 Winter Edition） - Blog - Qingyu✨'s blog

【欢迎投稿】一文概括所有比赛注意事项，以及同类资料推荐 - 洛谷专栏

Linux 相关

虚拟机配置

如果需要用虚拟机，记得把配置调高一点，但是如果配置过高的话，虚拟机可能无法启动。参考的参数是四核、4GB。另外记得检查一下共享文件夹是否存在。

.gdbinit

set max-value-size unlimited

unlimited 可以换成一个整数，单位是字节。

.vimrc

用 vim 打开 ~/.vimrc 后首先输入 :0r $VIMRUNTIME/vimrc_example.vim，可以适当使用 tab 补全，输入 :0r $VIMR<TAB>/v<TAB> 然后回车就可以了，注意这个步骤是重要的，不可忽略。然后是 tab 四件套 + nu sm cin fdm + 三个 map：

set ts=2 sw=2 sts=2 et nu sm cin fdm=marker
map <C-K> <C-V>
nnoremap j gj
nnoremap k gk

另外有几个难绷的补丁。

  • 解除 vim 复制最多 50 行的限制：set viminfo='1000,<500。
  • 解决 vim 输入 O 会卡一下的问题：set tm=10（数字可以更小）

.bashrc

如果主机名太长以至于感觉严重影响使用体验，可以输入 :%s/\\h/localhost。然后末尾加入：

alias python=python3
alias calc=gcalccmd
alias gdb='gdb -q'
alias rm='rm -i'
alias cp='cp -i'
alias mv='mv -i'

backup.sh

#!/bin/bash
dst=`dirname $0`/tmp/`date +%H-%M-%S`
mkdir -p $dst
for p in; do
  src=`dirname $0`/$p/$p.cpp
  if [ -e $src ]; then
    cp $src $dst
    if g++ $src -o /dev/null -std=c++14 -O2; then
      echo Problem $p: ok
    else
      echo Problem $p: CE
    fi
  else
    echo Problem $p: not found
  fi
done

dp.sh

#!/bin/bash
p=`basename $PWD`
make bf $p || exit 1
for i in {1..524288}; do
  echo Testcase $i is running...
  ./dt.py > 0.in
  ./bf <0.in >0.ans
  ./$p <0.in >0.out
  diff 0.out 0.ans || exit 1
done

makefile

main: $(shell basename $$PWD).cpp
    g++ $< -o $@ -g -DNF -O0 -DLOCAL -fsanitize=undefined,address -D_GLIBCXX_DEBUG
%: %.cpp
    g++ $< -o $@ -g -DNF -O2 -Wall -Wconversion -Wextra -Wshadow -std=c++14 -pg

selfeval.sh

#!/bin/bash
p=`basename $PWD`
make $p || exit 1
ulimit -v 512000
ulimit -s 512000
ulimit -t 5
for f in `find . -name '*.in'`; do
  echo -e "\e[36mtest: $f\e[0m"
  \time ./$p < $f | diff - ${f%.*}.ans -sqBZ
done

diff 的选项解释： -Z 是忽略行末空格，-B 是忽略全空行（为了忽略文末回车）。-s 会在文件相同时报告，-q 会在文件不同时报告。

使用 echo -e "\e[36m文字\e[0m" 为“文字”染上 36 号颜色（青色）。

缺省源

template.cpp

#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define endl "\n"
#define debug(...) void(0)
#endif
using LL = long long;
int main() {
#ifndef LOCAL
  cin.tie(nullptr)->sync_with_stdio(false);
#endif
  return 0;
}

modint.min.hpp

template <unsigned umod>
struct modint {/*{{{*/
  static constexpr int mod = umod;
  unsigned v;
  modint() = default;
  template <class T, enable_if_t<is_integral<T>::value, int> = 0>
    modint(const T& y) : v((unsigned)(y % mod + (is_signed<T>() && y < 0 ? mod : 0))) {}
  modint& operator+=(const modint& rhs) { v += rhs.v; if (v >= umod) v -= umod; return *this; }
  modint& operator-=(const modint& rhs) { v -= rhs.v; if (v >= umod) v += umod; return *this; }
  modint& operator*=(const modint& rhs) { v = (unsigned)(1ull * v * rhs.v % umod); return *this; }
  modint& operator/=(const modint& rhs) { assert(rhs.v); return *this *= qpow(rhs, mod - 2); }
  friend modint operator+(modint lhs, const modint& rhs) { return lhs += rhs; }
  friend modint operator-(modint lhs, const modint& rhs) { return lhs -= rhs; }
  friend modint operator*(modint lhs, const modint& rhs) { return lhs *= rhs; }
  friend modint operator/(modint lhs, const modint& rhs) { return lhs /= rhs; }
  template <class T> friend modint qpow(modint a, T b) {
    modint r = 1;
    for (assert(b >= 0); b; b >>= 1, a *= a) if (b & 1) r *= a;
    return r;
  }
  friend int raw(const modint& self) { return self.v; }
  friend ostream& operator<<(ostream& os, const modint& self) { return os << raw(self); }
  explicit operator bool() const { return v != 0; }
  modint operator-() const { return modint(0) - *this; }
  bool operator==(const modint& rhs) const { return v == rhs.v; }
  bool operator!=(const modint& rhs) const { return v != rhs.v; }
};/*}}}*/

曾经出过将 enable_if_t 写成 enable_if 的事故。如果拿捏不准不如不写。

线性代数

行列式

\[\operatorname{det}(A)=\sum_p(-1)^{\operatorname{sgn}(p)}\prod_{i}A[i][p_i]. \]

  • 交换两行，行列式变号。
  • 某一行乘以 \(t\)，行列式值乘以 \(t\)。
  • 有两行相同，行列式为 \(0\)。
  • 用一行的倍数加到另一行，行列式不变。

柯西-比内公式

对于大小为 \(m\times n\) 的矩阵 \(A\) 和大小为 \(n\times m\) 的矩阵 \(B\)，柯西-比内（Binet-Cauchy）公式指出：

\[\operatorname{det}(AB)=\sum_{|S|=m, S\subseteq [n]}\operatorname{det}(A_{[m], S})\operatorname{det}(B_{S,[m]}) \]

注：\(m>n\) 时可以推出 \(AB\) 不满秩，此时行列式为 \(0\)。

代数余子式

对于 \(n\times n\) 的方阵 \(A\)，定义 \(A\) 划去第 \(i\) 行第 \(j\) 列的行列式乘上 \((-1)^{i+j}\) 为 \(a_{i,j}\) 的代数余子式，记作 \(A_{i,j}=(-1)^{i+j}A_{[n]\setminus\{i\}, [n]\setminus\{j\}}\)。

有如下定理，不知道为什么：

  1. \[\forall i, \sum_{j=1}^na_{ij}A_{ij}=|A| \]

  2. \[\forall j, \sum_{i=1}^na_{ij}A_{ij}=|A| \]

  3. \[\forall i\neq k, \sum_{j=1}^na_{ij}A_{kj}=0 \]

  4. \[\forall j\neq k, \sum_{j=1}^na_{ij}A_{ik}=0 \]

矩阵树定理

无向图：度数矩阵 \(-\) 邻接矩阵，划去第 \(k\) 行第 \(k\) 列的行列式（整数 \(k\) 任意）。

有向图：根向树的度数矩阵是每个点的出度。外向树的度数矩阵是每个点的入度。划去 \(k\) 则根为 \(k\)。

BEST 定理

有向图 \(G\) 的欧拉回路条数为 \(T\prod_{x\in V}(deg_x-1)!\)。其中 \(T\) 是任意一点为根的根向生成树个数，可以证明任意一个答案都相同。\(deg_x\) 是入度和出度随便取一个。需要保证存在欧拉回路。

LGV 引理

\[\begin{vmatrix} e(A_1,B_1)&e(A_1,B_2)&\cdots&e(A_1,B_n)\\ e(A_2,B_1)&e(A_2,B_2)&\cdots&e(A_2,B_n)\\ \vdots&\vdots&\ddots&\vdots\\ e(A_n,B_1)&e(A_n,B_2)&\cdots&e(A_n,B_n) \end{vmatrix}=\sum_{S:A\to B}(-1)^{\operatorname{sgn}(\sigma(S))}\prod_{i=1}^n w(P_i). \]

其中 \(S=\{P_1, P_2, \cdots P_n\}\) 为一组不相交的路径。\(e(\circ, \circ)\) 是路径方案数。

数论（约数）

积性函数

将以上看到的几个函数放在一起得到两条链，链上的一条边如 \(I\to Id\) 表示 \(I*I=Id, Id*\mu=I\)，往右走 \(*I\)，往左走 \(*\mu\)。其实已经有一点接近贝尔级数了。

  1. \(\mu\to\epsilon\to I\to d\)
  2. \(\varphi\to Id\)

MR & PR

LL qmul(LL a, LL b, LL n) { return (LL)((__int128)a * b % n); }
LL qpow(LL a, LL b, LL n) {
  LL r = 1;
  while (b) {
    if (b & 1) r = qmul(r, a, n);
    if (b >>= 1) a = qmul(a, a, n);
  }
  return r;
}
bool isprime(LL n) {
  if (n <= 2) return n == 2;
  LL d = n - 1, r = __builtin_ctzll(d);
  d >>= r;
  for (LL a : {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37}) {
    if (n % a == 0) return n == a;
    LL k = qpow(a, d, n);
    if (k == 1) continue;
    bool flag = false;
    for (int i = 1; i <= r && !flag; i++, k = qmul(k, k, n)) flag |= k == n - 1;
    if (!flag) return false;
  }
  return true;
}
mt19937_64 rng64{random_device{}()};
map<LL, int> divide(LL n) {
  if (n <= 1) return {};
  if (n == 4) return {{2, 2}}; // !!!
  if (isprime(n)) return {{n, 1}};
  LL d = 1;
  while (d <= 1) {
    auto f = [n, c = rng64() % (n - 1) + 1](LL x) { return (qmul(x, x, n) + c) % n; };
    LL l = f(0), r = f(l);
    do {
      LL p = 1;
      for (int i = 0; i < 127 && l != r; i++) {
        LL q = qmul(p, abs(l - r), n);
        if (!q) break;
        p = q, l = f(l), r = f(f(r));
      }
      d = gcd(p, n);
      if (d > 1) break;
    } while (l != r);
  }
  int c = 0;
  while (n % d == 0) n /= d, ++c;
  auto res = divide(n);
  for (auto e : divide(d)) res[e.first] += e.second * c;
  return res;
}

剩余系划分

在 \(n\) 个点的图中，点集为 \(\{0, 1, \cdots, n-1\}\)。若将 \(i\) 与 \((i+d)\bmod n\) 连边，则得到 \(\gcd(n, d)\) 个长为 \(n/\gcd(n, d)\) 的环。（提示：代入 \(d=1\)）

单位根及反演

设 \(\omega_n\) 为 \(n\) 次本原单位根，则有（可以代入 \(x=-1\) 等神秘数字）

\[x^n-1=\prod_{i=0}^{n-1}(x-\omega_n^i) \]

以下是单位根反演，其实质为 DFT 与 IDFT。

\[[n|k]=\frac{1}{n}\sum_{i=0}^{n-1}\omega_n^{ik} \]

如果有素数 \(p\) 和正整数 \(m\) 满足 \(m|(p-1)\)，则可以在 \(\mathbb F_p\) 下找到 \(m\) 次本原单位根（即原根的 \((p-1)/m\) 次方）。

若 \(m\) 极小，则可以扩域维护每个数为 \(f_0+f_1w+f_2w^2+\cdots+f_{m-1}w^{m-1}\) 的形式，最后将这个多项式模 \(m\) 级分圆多项式 \(\Phi_m(w)\) 获得真实值。

分圆多项式

\(m\) 级分圆多项式 \(\Phi_m(x)\) 是一个在 \(\mathbb Z[x]\) 上 \(\varphi(m)\) 次的不可约首一多项式，满足

\[\Phi_n(x)=(x-w_1)(x-w_2)\cdots(x-w_{\varphi(n)})=\prod_{i=0}^{n-1}(x-w^i)^{[\gcd(i, n)=1]} \]

其中 \(w_1, w_2, \cdots, w_{\varphi(n)}\) 是全部 \(n\) 次本原单位根，\(w\) 在 \(w_1, w_2, \cdots, w_{\varphi(n)}\) 中任取。根据一些资料可以得知：

\[\prod_{d|n}\Phi_d(x)=x^n-1 \]

\[\Phi_n(x)=(-1)^{[n=1]}\prod_{d|n}(1-x^d)^{\mu(n/d)} \]

数论（同余）

Cipolla 求二次剩余

给定 \(c, p\)，\(p\) 为奇质数，求解关于 \(x\) 的同余方程 \(x^2\equiv c\pmod p\)。

欧拉判别：对于任意 \(c\)，\(c^{(p-1)/2}\equiv \pm 1\pmod p\)。当且仅当 \(c\) 有二次剩余时，\(c^{(p-1)/2}\equiv 1\pmod p\)。

Cipolla 过程：随机一个 \(a\)，使得 \(a^2-c\) 没有二次剩余（期望 \(O(1)\) 次找到）。定义 \(\mathbf i\)，满足 \(\mathbf i^2 = a^2 - c\)。则 \(x_1=(a+\mathbf i)^{(p+1)/2}\)，另一个解是它的相反数。

exgcd

LL mod(LL x, LL m) { return (x % m + m) % m; }
LL exgcd(LL a, LL b, LL c, LL& x, LL& y) {
  if (!b) return x = c / a, y = 0, a;
  LL res = exgcd(b, a % b, c, y, x);
  return y -= a / b * x, res;
}
LL solve(LL a, LL b, LL c) {
  LL x, y, d = exgcd(a, b, c, x, y);
  return c % d == 0 ? mod(x, b / d) : -1;
}

调用 solve(a, b, c) 能求得 \(ax+by=c\) 中 \(x\) 的最小非负整数解，无解返回 \(−1\)。

CRT

适用范围：\(a_1,a_2,\cdots,a_n\) 两两互质。

做法：令 \(M=\prod a_i,m_i=M/a_i\)，然后 \(t_i\) 是 \(m_i\) 在模 \(a_i\) 意义下的逆元。

答案是 \(x=\sum b_im_it_i\)。对 \(M\) 取模。

原根

欧拉定理：对于 \((a,m)=1\)，\(a^{\varphi(m)}\equiv 1\pmod m\)。

一个数模 \(m\) 的阶存在，那么它一定是 \(\varphi(m)\) 的约数。

模 \(m\) 的原根：模 \(m\) 的阶为 \(\varphi(m)\) 的数。设为 \(g\)。\(m\) 是质数时，\(g^t\) 和 \([1,m-1]\) 形成双射。

一个数 \(m\) 存在原根当且仅当 \(m=2,4,p^a,2p^a\) 其中 \(p\) 为奇素数。最小原根的大小为 \(O(m^{\frac{1}{4}})\)。

Lucas

对于质数 \(P\) 有

\[\binom n m\equiv \binom{\left\lfloor n/P\right\rfloor}{\left\lfloor m/P\right\rfloor}\binom{n\bmod P}{m\bmod P}\pmod P \]

数论（整除）

杜教筛

若 \(f*g=h\)，则（大写表示前缀和）

\[H(n)=\sum_{i=1}^nf(i)G(n/i) \]

\[g(1)F(n)=\sum_{i=1}^n g(i)F(n/i)-\sum_{i=2}^n g(i)F(n/i)=H(n)-\sum_{i=2}^ng(i)F(n/i). \]

如果预处理 \(O(n^{2/3})\) 的函数 \(F\) 点值（注意一定要预处理）那么复杂度为 \(O(n^{2/3})\)。

万能欧几里得

\(\text{solve}(p, q, r, l, U, R)\) 表示对直线 \(y=\dfrac{px+r}{q}\ \left(x\in(0, l], 0\leq r<q\right)\) 上，每次碰到横线执行 \(U\) 操作，碰到竖线执行 \(R\) 操作，规定整点上先 \(U\) 再 \(R\)。

\[\text{solve}(p, q, r, l, U, R) =\begin{cases} \varnothing, \text{when}\ l=0; \\ \text{solve}(p\bmod q, q, r, l, U, U^{\left\lfloor p/q\right\rfloor}R), \text{when}\ p\geq q;\\ \text{let}\ m=\left\lfloor\dfrac{pl+r}{q}\right\rfloor\ \text{in}\begin{cases} R^l, \text{when}\ m=0;\\ R^{\left\lfloor(q-r-1)/p\right\rfloor}U\cdot \text{solve}(q, (q-r-1)\bmod p, p, m-1, R, U)\\ \quad\quad \times R^{l-\left\lfloor(qm-r-1)/p\right\rfloor}, \text{otherwise}. \end{cases} \end{cases} \]

这个不会考，考了也做不了。

多项式

求导公式

后面要反复使用，默认所求导的元是 \(x\)，即 \(F'(x)\) 这个记号说的是 \(\dfrac{\mathrm d}{\mathrm dx}F(x)\)，这个非常重要！

\[(x^n)'=nx^{n-1} \]

\[(F(x)\pm G(x))'=F'(x)+G'(x) \]

\[(F(x)G(x))'=F'(x)G(x)+F(x)G'(x) \]

\[\left(\frac{F(x)}{G(x)}\right)'=\frac{F'(x)G(x)-F(x)G'(x)}{G(x)^2} \]

\[(F(G(x)))'=F'(G(x))G'(x) \]

\[\exp' x=\exp x \]

\[\ln' x=\frac{1}{x}\implies (\ln(1+x))'=\ln'(1+x)\times 1=\frac{1}{1+x} \]

牛顿迭代

给出 \(G(H(x))\)，我们需要找到 \(H(x)\) 使得 \(G(H(x))=0\)。

设 \(n\) 为偶数，已经知道了 \(H_*(x)=H(x)\bmod{x^{n/2}}\) 满足 \(G(H_*(x))\equiv 0\pmod{x^{n/2}}\)（\(H(0)\) 需要特殊计算）。想知道 \(H(x)\bmod x^{n}\)。

\[H(x)\equiv H_*(x)-\dfrac{G(H_*(x))}{\dfrac{\mathrm d}{\mathrm dH_*(x)}G(H_*(x))}\pmod {x^n} \]

NTT（DIF-DIT）

DIT 记得写 reverse(a.begin() + 1, a.end()); 和除以 \(n\)。

int glim(size_t x) { return x == 1 ? 1 : 2 << __lg(x - 1); }
using poly = vector<mint>;
vector<mint> wt;
vector<mint>& ntt_init(int n) {
  auto &w = wt;
  if (w.empty()) w = {1};
  while ((int)w.size() < n) {
    int m = (int)w.size();
    mint wn = qpow(mint(3), (mint::mod - 1) / m >> 2);
    w.resize(m << 1);
    for (int i = m; i < m << 1; i++) w[i] = wn * w[i ^ m];
  }
  return w;
}
valarray<mint> dif(const poly& src, int n) {
  auto &w = ntt_init(n);
  valarray<mint> a(mint(0), n);
  copy(src.begin(), src.end(), &a[0]);
  for (int len = n, k = n >> 1; k >= 1; len >>= 1, k >>= 1) {
    for (int i = 0, t = 0; i < n; i += len, t++) {
      for (int j = 0; j < k; j++) {
        auto x = a[i + j], y = a[i + j + k] * w[t];
        a[i + j] = x + y, a[i + j + k] = x - y;
      }
    }
  }
  return a;
}
poly dit(const valarray<mint>& src) {
  int n = (int)src.size();
  auto &w = ntt_init(n);
  poly a(begin(src), end(src));
  for (int k = 1, len = 2; len <= n; k <<= 1, len <<= 1) {
    for (int i = 0, t = 0; i < n; i += len, t++) {
      for (int j = 0; j < k; j++) {
        auto x = a[i + j], y = a[i + j + k];
        a[i + j] = x + y, a[i + j + k] = (x - y) * w[t];
      }
    }
  }
  mint iv = mint::mod - (mint::mod - 1) / n;
  for (int i = 0; i < n; i++) a[i] *= iv;
  reverse(a.begin() + 1, a.end());
  return a;
}

拉格朗日插值

\[\ell_j(x)=\prod_{i\neq j}\frac{x-x_i}{x_j-x_i} \]

\[f(x)=\sum_i\ell_i(x)y_i \]

NTT 模数

  • \(167772161 = 5 \times 2^ {25} + 1\) 的原根为 $ g = 3$。
  • \(469762049 = 7 \times 2^ {26} + 1\) 的原根为 $ g = 3$。
  • \(998244353 = 119 \times 2^ {23} + 1\) 的原根为 $ g = 3$。
  • \(1004535809 = 479 \times 2^ {21} + 1\) 的原根为 $ g = 3$。

Chirp-Z 变换（CZT）

\[ij=\binom{i+j}{2}-\binom i 2-\binom j 2 \]

字符串（线性算法）

kmp

void kmp(char *s, int fail[]) {
  int n = strlen(s + 1);
  fail[1] = 0;
  for (int i = 2, j = 0; i <= n; i++) {
    while (j && s[j + 1] != s[i]) j = fail[j];
    j += s[j + 1] == s[i];
    fail[i] = j;
  }
}

exkmp

void exkmp(int len) {
  z[1] = len;
  for (int i = 2, l = 0, r = 0; i <= len; i++) {
    if (i <= r) z[i] = min(z[i - l + 1], r - i + 1);
    while (i + z[i] <= len && a[1 + z[i]] == a[i + z[i]]) ++z[i];
    if (i + z[i] - 1 > r) r = i + z[l = i] - 1;
  }
}

manacher

void manacher() {
  for (int i = 1, mid = 0, r = 0; i <= n; i++) {
    if (i <= r) pal[i] = min(pal[mid * 2 - i], r - i + 1);
    while (a[i - pal[i]] == a[i + pal[i]]) ++pal[i];
    if (i + pal[i] - 1 > r) r = i + pal[mid = i] - 1;
  }
}

Lyndon 分解

题解 P6127 【模板】Lyndon 分解：如果 \(s\) 是其所有后缀中最小的字符串，则 \(s\) 是 Lyndon 串。

该算法中我们仅需维护三个变量 \(i,j,k\)。

维持一个循环不变式：

  • \(s[:i-1]=s_1s_2\cdots s_g\) 是固定下来的分解，也就是 \(\forall l\in[1,g],s_l\) 是 \(\text{Lyndon}\) 串且 \(s_l>s_{l+1}\)。
  • \(s[i,k-1]=t^h+v(h>1)\) 是没有固定的分解，满足 \(t\) 是 \(\text{Lyndon}\) 串，且 \(v\) 是 \(t\) 的可为空的不等于 \(t\) 的前缀，且有 \(s_g>s[i,k-1]\)

设当前读入的字符是 \(s[k]\)，令 \(j=k-|t|\)。

分三种情况讨论：

  • 当 \(s[k]=s[j]\) 时，直接 \(k\leftarrow k+1,j\leftarrow j+1\)，周期 \(k-j\) 继续保持
  • 当 \(s[k]>s[j]\) 时，由引理 2 可知 \(v+s[k]\) 是 \(\text{Lyndon}\) 串，由于 \(\text{Lyndon}\) 分解需要满足 \(s_i\ge s_{i+1}\)，所以不断向前合并，最终整个 \(t^h+v+s[k]\) 形成了一个新的 \(\text{Lyndon}\) 串。
  • 当 \(s[k]<s[j]\) 时，\(t^h\) 的分解被固定下来，算法从 \(v\) 的开头处重新开始。
for (int i = 0; i < n; ) {
  int j = i, k = i + 1;
  while (k < n && str[j] <= str[k]) {
    if (str[j] < str[k]) j = i;
    else j++;
    k++;
  }
  while (i <= j) /*[i, i + k - j),*/ i += k - j;
}

字符串（自动机）

自动机 状态集合 Link 树（若 \(link_y=x\)）
SAM 原串的所有子串 则等价类 \(x\) 是等价类 \(y\) 的后缀
ACAM 所有字符串的前缀 则前缀 \(x\) 是前缀 \(y\) 的后缀
PAM 所有回文串 则回文子串 \(x\) 是回文子串 \(y\) 的后缀

广义 SAM

点击查看代码 
template <int N, int M> struct suffixam {
 int link[N << 1], len[N << 1], ch[N << 1][M], tot;
 suffixam() : tot(1) {}
 int split(int p, int q, int r) {
  if (len[q] == len[p] + 1) return q;
  int u = ++tot;
  len[u] = len[p] + 1;
  memcpy(ch[u], ch[q], sizeof ch[u]);
  link[u] = link[q], link[q] = u;
  for (; p && ch[p][r] == q; p = link[p]) ch[p][r] = u;
  return u;
 }
 int expand(int p, int r) {
  int u = ++tot;
  memset(ch[u], 0, sizeof ch[u]);
  len[u] = len[p] + 1;
  for (; p; p = link[p]) {
   if (!ch[p][r]) ch[p][r] = u;
   else return link[u] = split(p, ch[p][r], r), u;
  }
  link[u] = 1;
  return u;
 }
};

AC 自动机

点击查看代码 
template <int N, int M> struct ACAM {
  int ch[N][M], tot, fail[N];
  void insert(const string& str) {
    int u = 0;
    for (char c : str) {
      int &v = ch[u][c - 'a'];
      v ? u = v : u = v = ++tot;
    }
  }
  void build() {
    queue<int> q;
    for (int i = 0; i < M; i++) if (ch[0][i]) q.push(ch[0][i]);
    while (!q.empty()) {
      int u = q.front(); q.pop();
      for (int i = 0; i < M; i++) {
        if (ch[u][i]) fail[ch[u][i]] = ch[fail[u]][i], q.push(ch[u][i]);
        else ch[u][i] = ch[fail[u]][i];
      }
    }
  }
};

PAM

点击查看代码 
template <int N, int M>
struct palindam {
  int str[N + 10], cnt, ch[N + 10][M], fail[N + 10], len[N + 10], dep[N + 10], tot;
  palindam() : cnt(0), tot(1) { 
    memset(ch[0], 0, sizeof ch[0]);
    memset(ch[1], 0, sizeof ch[1]);
    fail[0] = 1;
    len[1] = -1;
    str[0] = -1;
  }
  int getfail(int p) {
    while (cnt - len[p] - 1 < 1 || str[cnt - len[p] - 1] != str[cnt])
      p = fail[p];
    return p;
  }
  int expand(int p, int r) {
    str[++cnt] = r;
    p = getfail(p);
    if (ch[p][r]) return ch[p][r];
    int u = ++tot;
    memset(ch[u], 0, sizeof ch[u]);
    len[u] = len[p] + 2;
    fail[u] = ch[getfail(fail[p])][r];
    dep[u] = dep[fail[u]] + 1;
    ch[p][r] = u;
    return u;
  }
};
// 插入从 lst = 1 或 lst = 0 开始都对

字符串（后缀数组）

倍增后缀数组

点击查看代码（完全 vector） 
struct machine {// {{{
  int n;
  vector<int> rk, sa, st[30], buc, id;
  machine() = default;
  explicit machine(const string& str)
      : n((int)str.size()), rk(n + 1), sa(n), buc(max(n, 128)), id(n) {
    rk[n] = -1;
    for (int i = 0; i < n; i++) buc[rk[i] = str[i]] += 1;
    for (int i = 1; i < 128; i++) buc[i] += buc[i - 1];
    for (int i = n; i--;) sa[--buc[rk[i]]] = i;
    for (int j = 1; j <= n; j <<= 1) {
      int cur = 0;
      for (int i = n - j; i < n; i++) id[cur++] = i;
      for (int i = 0; i < n; i++)
        if (sa[i] >= j) id[cur++] = sa[i] - j;
      memset(buc.data(), 0, sizeof(int) * n);
      for (int i = 0; i < n; i++) buc[rk[i]] += 1;
      for (int i = 1; i < n; i++) buc[i] += buc[i - 1];
      for (int i = n; i--;) sa[--buc[rk[id[i]]]] = id[i];
      id[0] = 0;
      auto pred = [&](int x, int y) {
        return rk[x] != rk[y] || rk[x + j] != rk[y + j];
      };
      int pre = id[sa[0]] = 0;
      for (int i = 1; i < n; i++) id[sa[i]] = (pre += pred(sa[i - 1], sa[i]));
      memcpy(rk.data(), id.data(), sizeof(int) * n);
      if (pre + 1 == n) break;
    }
    auto& lcp = st[0];
    lcp.resize(n - 1);
    for (int i = 0, h = 0; i < n; i++) {
      if (!rk[i]) continue;
      if (h) h -= 1;
      int j = sa[rk[i] - 1];
      while (max(i, j) + h < n && str[i + h] == str[j + h]) h += 1;
      lcp[rk[i] - 1] = h;
    }
    for (int j = 1; 1 << j <= n; j++) {
      st[j].resize(n - (1 << j));
      for (int i = 0; i + (1 << j) < n; i++) {
        st[j][i] = min(st[j - 1][i], st[j - 1][i + (1 << (j - 1))]);
      }
    }
  }
  int operator()(int i, int j) const {
    if (max(i, j) == n) return 0;
    if (i == j) return n - i;
    int l = min(rk[i], rk[j]), r = max(rk[i], rk[j]) - 1;
    int k = __lg(r - l + 1);
    return min(st[k][l], st[k][r - (1 << k) + 1]);
  }
};// }}}

Runs

可以改成 hash。

点击查看代码 
struct run {
  int l, r, p;
  bool operator<(const run& rhs) const {
    return l != rhs.l ? l < rhs.l : r < rhs.r;
  }
  bool operator==(const run& rhs) const {
    return l == rhs.l && r == rhs.r && p == rhs.p;
  }
};
vector<run> getRuns(string s) {
  int n = (int)s.size();
  auto lcp = machinenew(s);
  reverse(begin(s), end(s));
  auto lcs = machinenew(s);
  reverse(begin(s), end(s));
  s += '\0';
  vector<run> ans;
  for (int op : {0, 1}) {
    vector<int> stk;
    for (int i = n - 1; i >= 0; i--) {
      while (!stk.empty()) {
        int u = i, v = stk.back(), len = lcp(u, v);
        if ((s[u + len] < s[v + len]) == op) stk.pop_back();
        else break;
      }
      if (!stk.empty()) {
        int l = i, r = stk.back(), tr = lcp(l, r), tl = lcs(n - l - 1, n - r - 1);
        if (tl + tr >= r - l + 1) ans.push_back({.l = l - tl + 1, .r = r + tr - 1, .p = r - l});
      }
      stk.push_back(i);
    }
  }
  auto bg = begin(ans), ed = end(ans);
  sort(bg, ed), ans.erase(unique(bg, ed), ed);
  return ans;
}

数据结构（平衡树）

分裂合并 WBLT

点击查看代码 
template <int N>
struct wblt {
  int ch[N << 1][2], tsh[N << 1], tot = 0, cnt = 0, siz[N << 1], val[N << 1];
  int newnode(int v) {
    int p = cnt ? tsh[cnt--] : ++tot;
    ch[p][0] = ch[p][1] = 0, siz[p] = 1, val[p] = v, maintain(p);
    return p;
  }
  bool isleaf(int p) { return !ch[p][0]; }
  void maintain(int p) {
    if (isleaf(p)) return;
    val[p] = val[ch[p][1]], siz[p] = siz[ch[p][0]] + siz[ch[p][1]];
  }
  int mg(int p, int q) {
    if (!p || !q) return p + q;
    int lim = 0.292 * (siz[p] + siz[q]);
    if (min(siz[p], siz[q]) >= lim) {
      int t = newnode(val[p]);
      ch[t][0] = p, ch[t][1] = q;
      return maintain(t), t;
    }
    if (siz[p] >= siz[q]) {
      // pushdown(p);
      auto [x, y] = ch[tsh[++cnt] = p];
      if (siz[x] >= lim) return mg(x, mg(y, q));
      // pushdown(y);
      auto [y0, y1] = ch[tsh[++cnt] = y];
      return mg(mg(x, y0), mg(y1, q));
    } else {
      // pushdown(q);
      auto [x, y] = ch[tsh[++cnt] = q];
      if (siz[y] >= lim) return mg(mg(p, x), y);
      auto [x0, x1] = ch[tsh[++cnt] = x];
      // pushdown(x);
      return mg(mg(p, x0), mg(x1, y));
    }
  }
  void sp(int p, int k, int& x, int& y) {
    if (!k) return x = 0, y = p, void();
    if (isleaf(p)) return x = p, y = 0, assert(k == 1);
    // pushdown(p);
    if (k <= siz[ch[p][0]])
      sp(ch[p][0], k, x, y), y = mg(y, ch[p][1]);
    else
      sp(ch[p][1], k - siz[ch[p][0]], x, y), x = mg(ch[p][0], x);
    tsh[++cnt] = p;
  }
  void spv(int p, int v, int& x, int& y) {
    if (val[p] <= v) return x = p, y = 0, void();
    if (isleaf(p)) return x = 0, y = p, void();
    // pushdown(p);
    if (v < val[ch[p][0]])
      spv(ch[p][0], v, x, y), y = mg(y, ch[p][1]);
    else
      spv(ch[p][1], v, x, y), x = mg(ch[p][0], x);
    tsh[++cnt] = p;
  }
  int getkth(int p, int k) {
    while (!isleaf(p)) {
      // pushdown(p);
      if (k <= siz[ch[p][0]])
        p = ch[p][0];
      else
        k -= siz[ch[p][0]], p = ch[p][1];
    }
    return val[p];
  }
  void dfs(int p, int& lst) {
    if (!isleaf(p))
      dfs(ch[p][0], lst), dfs(ch[p][1], lst);
    else
      assert(exchange(lst, val[p]) <= val[p]);
  }
};

fhqtreap

点击查看代码 
mt19937 rng(random_device{}());
template <int N>
struct fhqtreap {
  int ch[N + 10][2], tot, val[N + 10], pri[N + 10], siz[N + 10], x, y, z, root;
  int newnode(int v) {
    int p = ++tot;
    return ch[p][0] = ch[p][1] = 0, pri[p] = rng(), val[p] = v, siz[p] = 1, p;
  }
  void maintain(int p) { siz[p] = siz[ch[p][0]] + 1 + siz[ch[p][1]]; }
  fhqtreap() : tot(-1), root(0) { newnode(0), siz[0] = 0; }
  int merge(int p, int q) {
    if (!p || !q) return p + q;
    if (pri[p] < pri[q])
      return ch[p][1] = merge(ch[p][1], q), maintain(p), p;
    else
      return ch[q][0] = merge(p, ch[q][0]), maintain(q), q;
  }
  void split(int p, int v, int &x, int &y) {
    if (!p) return x = y = 0, void();
    if (val[p] <= v)
      x = p, split(ch[p][1], v, ch[p][1], y), maintain(p);
    else
      split(ch[p][0], v, x, ch[p][0]), y = p, maintain(p);
  }
  int find(int v, int p) {
    if (val[p] == v) return p;
    return val[p] <= v ? find(v, ch[p][1]) : find(v, ch[p][0]);
  }
  void insert(int v) {
    split(root, v, x, y);
    root = merge(x, merge(newnode(v), y));
  }
  void erase(int v) {
    split(root, v - 1, x, y), split(y, v, y, z);
    root = merge(merge(x, ch[y][0]), merge(ch[y][1], z));
  }
  int getrnk(int v) {
    split(root, v - 1, x, y);
    int res = siz[x] + 1;
    root = merge(x, y);
    return res;
  }
  int getkth(int k, int p) {
    int c = siz[ch[p][0]] + 1;
    if (c == k)
      return val[p];
    else
      return c < k ? getkth(k - c, ch[p][1]) : getkth(k, ch[p][0]);
  }
  int getpre(int v) {
    split(root, v - 1, x, y);
    int p = x;
    while (ch[p][1]) p = ch[p][1];
    root = merge(x, y);
    return val[p];
  }
  int getsuf(int v) {
    split(root, v, x, y);
    int p = y;
    while (ch[p][0]) p = ch[p][0];
    root = merge(x, y);
    return val[p];
  }
};

splay & lct

点击查看代码 
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long LL;
template <int N>
struct lctree {
  int val[N + 10], sum[N + 10], fa[N + 10], ch[N + 10][2], rev[N + 10];
  bool getson(int p) { return ch[fa[p]][1] == p; }
  bool isroot(int p) { return !p || ch[fa[p]][getson(p)] != p; }
  void maintain(int p) { sum[p] = val[p] ^ sum[ch[p][0]] ^ sum[ch[p][1]]; }
  void pushdown(int p) {
    if (rev[p])
      swap(ch[p][0], ch[p][1]), rev[ch[p][0]] ^= 1, rev[ch[p][1]] ^= 1,
          rev[p] ^= 1;
  }
  void update(int p) {
    if (!isroot(p)) update(fa[p]);
    pushdown(p);
  }
  void connect(int p, int q, int r) { fa[p] = q, ch[q][r] = p; }  // p->q
  void rotate(int p) {
    int f = fa[p], r = getson(p);
    if (fa[p] = fa[f], !isroot(f)) connect(p, fa[f], getson(f));
    connect(ch[p][r ^ 1], f, r), connect(f, p, r ^ 1), maintain(f), maintain(p);
  }
  void splay(int p) {
    for (update(p); !isroot(p); rotate(p))
      if (!isroot(fa[p])) rotate(getson(p) == getson(fa[p]) ? fa[p] : p);
  }
  int access(int p) {
    int y = 0;
    for (; p; p = fa[y = p]) splay(p), ch[p][1] = y, maintain(p);
    return y;
  }
  void makeroot(int p) { access(p), splay(p), rev[p] ^= 1; }
  int findroot(int p) {
    access(p), splay(p);
    while (ch[p][0]) p = ch[p][0];
    return p;
  }
  void split(int x, int y) { makeroot(x), access(y), splay(y); }
  void link(int x, int y) { makeroot(x), fa[x] = y; }
  void cut(int x, int y) {
    split(x, y);
    if (fa[x] == y && !ch[x][1]) fa[x] = ch[y][0] = 0;
    maintain(y);
  }
  void modify(int x, int y) { splay(x), val[x] = y, maintain(x); }
  int lca(int x, int y) { return access(x), access(y); }
};
int n, m;
lctree<100010> t;
int main() {
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= n; i++) scanf("%d", &t.val[i]), t.sum[i] = t.val[i];
  for (int i = 1, op, x, y; i <= m; i++) {
    scanf("%d%d%d", &op, &x, &y);
    switch (op) {
      case 0:
        t.split(x, y), printf("%d\n", t.sum[y]);
        break;
      case 1:
        if (t.findroot(x) != t.findroot(y)) t.link(x, y);
        break;
      case 2:
        if (t.findroot(x) == t.findroot(y)) t.cut(x, y);
        break;
      case 3:
        t.modify(x, y);
    }
  }
  return 0;
}

数据结构（更多的树）

左偏树

template <int N, class T>
struct leftree {
  int ch[N + 10][2], dis[N + 10], tot;
  T val[N + 10];
  leftree() : tot(0) { dis[0] = -1; }
  int newnode(T x) {
    int p = ++tot;
    return val[p] = x, ch[p][0] = ch[p][1] = 0, dis[p] = 0, p;
  }
  int merge(int p, int q) {
    if (!p || !q) return p + q;
    if (val[p].first > val[q].first) swap(p, q);
    ch[p][1] = merge(ch[p][1], q);
    if (dis[ch[p][0]] < dis[ch[p][1]]) swap(ch[p][0], ch[p][1]);
    dis[p] = dis[ch[p][1]] + 1;
    return p;
  }
};

李超树

template <class T>
struct func {
  T k, b;
  func(T k = 0, T b = 0) : k(k), b(b) {}
  T operator()(T x) { return k * x + b; }
};
template <int N, class T>
struct lcstree {
  func<T> tag[N + 10];
  int ch[N + 10][2], tot;
  lcstree() : tot(-1) { newnode(); }
  int newnode() {
    int p = ++tot;
    return ch[p][0] = ch[p][1] = 0, tag[p] = func<T>(), p;
  }
  void insert(func<T> f, int &p, int l = 1, int r = 4e8) {
    if (!p) p = newnode();
    int mid = (l + r) >> 1;
    switch ((f(l) <= tag[p](l)) + (f(r) <= tag[p](r))) {
      case 0:
        tag[p] = f;
        break;
      case 1:
        insert(f, ch[p][0], l, mid), insert(f, ch[p][1], mid + 1, r);
        break;
    }
  }
  T query(int x, int &p, int l = 1, int r = 4e8) {
    if (!p) return 0;
    int mid = (l + r) >> 1;
    if (x <= mid)
      return max(tag[p](x), query(x, ch[p][0], l, mid));
    else
      return max(tag[p](x), query(x, ch[p][1], mid + 1, r));
  }
};

计算几何

叉乘

T cross(const point &lhs, const point &rhs) {  // 叉积
  return lhs.x * rhs.y - rhs.x * lhs.y;
}

Graham 求凸包

bool cmp(const dot &a, const dot &b) {
  return cross(a, b) ? cross(a, b) > 0 : dist(a) < dist(b);
}
vector<dot> convexHull(vector<dot> a) {  // 凸包
  static dot stk[1 << 18];
  dot cen = *min_element(a.begin(), a.end());
  sort(a.begin(), a.end(),
       [&](const dot &a, const dot &b) { return cmp(a - cen, b - cen); });
  int top = 0;
  for (dot v : a) {
    while (top >= 2 && cross(stk[top - 1] - stk[top], v - stk[top]) > 0) top--;
    stk[++top] = v;
  }
  return vector<dot>(stk + 1, stk + top + 1);
}

Andrew 求凸包

bool operator<(const point &a, const point &b) {
  return a.x != b.x ? a.x < b.x : a.y < b.y;
}
auto makeConvex(vector<dot> vec) {  // 另一个版本，需要删掉三点共线，得到一侧凸包
  // assert(is_sorted(vec.begin(), vec.end()));
  vector<dot> ret;
  for (dot p : vec) {
    while (ret.size() >= 2 &&
           cross(ret.end()[-2] - ret.back(), p - ret.back()) <= 0)
      ret.pop_back();
    ret.push_back(p);
  }
  return ret;
}

minkowski 和

vector<dot> minkowski(const vector<dot> &a,
                      const vector<dot> &b) {  //闵可夫斯基和
  vector<dot> c = {a[0] + b[0]};
  static dot sa[1 << 18], sb[1 << 18];
  int n = a.size(), m = b.size();
  for (int i = 0; i < n; i++) sa[i] = a[(i + 1) % n] - a[i];
  for (int i = 0; i < m; i++) sb[i] = b[(i + 1) % m] - b[i];
  int i = 0, j = 0;
  for (int k = 1; k < n + m; k++) {
    if (i < n && (j >= m || cmp(sa[i], sb[j])))
      c.push_back(c.back() + sa[i++]);
    else
      c.push_back(c.back() + sb[j++]);
  }
  return c;
}

auto minkowski(vector<dot> a,
               vector<dot> b) {  // 另一个版本，注意必须叉掉三点共线
  if (a.empty()) return b;
  if (b.empty()) return a;
  for (int i = (int)a.size() - 1; i >= 1; i--) a[i] = a[i] - a[i - 1];
  for (int i = (int)b.size() - 1; i >= 1; i--) b[i] = b[i] - b[i - 1];
  vector<dot> c = {a[0] + b[0]};
  merge(a.begin() + 1, a.end(), b.begin() + 1, b.end(), back_inserter(c),
        [](dot p, dot q) { return cross(p, q) < 0; });
  for (int i = 1; i < (int)c.size(); i++) c[i] = c[i - 1] + c[i];
  return c;
}

图论

有向图缩点 / 强连通分量（SCC）

点击查看代码 
int dfn[1010], low[1010], stk[1010], col[1010], cnt, top, tot;
void reset() {
  cnt = 0;
  tot = 0;
  memset(dfn, 0, sizeof dfn);
  memset(col, 0, sizeof col);
}
void tarjan(int u) {
  low[stk[++top] = u] = dfn[u] = ++cnt;
  for (int i = g.head[u]; i; i = g.nxt[i]) {
    int v = g[i].v;
    if (!dfn[v])
      tarjan(v), low[u] = min(low[u], low[v]);
    else if (!col[v])
      low[u] = min(low[u], dfn[v]);
  }
  if (low[u] == dfn[u]) {
    col[u] = ++tot;
    while (stk[top] != u) col[stk[top--]] = tot;
    top--;
    // do col[stk[top]] = css; while (stk[top--] != u);
  }
}

补充：instack 问题。scc 中访问到 dfs 过的点时必须需要判断是否在栈内，在栈中时才更新 low。点双、边双好像没有这个要求，不过判了更好。

边双连通分量（ECC）

边双的定义：两个点 \(u, v\) 在无向图上连通，若删去图中的任意一条边，都不能使他们不连通，则说 \(u, v\) 边双连通。边双联通具有传递性。

在缩点的基础上，强制不让它走到父亲边即可。\(dfn_u=low_u\)。

我不知道为什么正经的做法都说是 \(low_v>dfn_u\)。但是这个代码真的能过。

点击查看代码 
graph<500010, 2000010> g;
int dfn[500010], low[500010], stk[500010], cnt, top, col[500010], dcc,
    siz[500010];
bool vis[2000010 << 1];
void tarjan(int u) {
  dfn[u] = low[stk[++top] = u] = ++cnt;
  for (int i = g.head[u]; i; i = g.nxt[i]) {
    if (vis[i] || vis[i ^ 1]) continue;
    int v = g[i].v;
    if (!dfn[v])
      vis[i] = vis[i ^ 1] = 1, tarjan(v), low[u] = min(low[u], low[v]);
    else
      low[u] = min(low[u], dfn[v]);
  }
  if (dfn[u] == low[u]) {
    col[u] = ++dcc;
    do col[stk[top]] = dcc;
    while (stk[top--] != u);
  }
}

点双连通分量（BCC）

点双的定义：两个点 \(u, v\) 在无向图上连通，若删去图中的任意一个不是 \(u, v\) 的点，都不能使他们不连通，则说 \(u, v\) 点双连通。点双联通不一定有传递性。

无向图割点的条件为：\(low_v\geq dfn_u\)，这样 \(v\) 这个儿子就走不到 \(u\)，割掉 \(u\)，\(v\) 就过不来了。

点双和割点一样的。但是为了求出点双连通分量需要开一个栈，还要注意一个点可能在多个点双内。

点击查看代码 
graph<500010, 2000010> g, t;
int dfn[500010], low[500010], stk[500010], cnt, top;
int dcc, cut[500010], siz[500010];
void tarjan(int u) {
  dfn[u] = low[stk[++top] = u] = ++cnt, cut[u] = 1;
  for (int i = g.head[u]; i; i = g.nxt[i]) {
    int v = g[i].v;
    if (!dfn[v]) {
      tarjan(v), low[u] = min(low[u], low[v]);
      if (low[v] >= dfn[u]) {
        cut[u]++, dcc++;
        do t.add(dcc, stk[top]);
        while (stk[top--] != v);
        t.add(dcc, u);
      }
    } else
      low[u] = min(low[u], dfn[v]);
  }
  if (!g.head[u]) t.add(++dcc, u);
}

图相关定理

  • 一般图：图的最大团 \(=\) 补图的最大独立集。
  • 一般图：最大独立集 \(+\) 最小点覆盖 \(=\) \(n\)。（最大独立集是最小点覆盖的补集）
  • 一般图：最小边覆盖 \(+\) 最大匹配数 \(=\) \(n\)。（这两个的方案可以互相转换，互相删删增增）
  • Hall 定理（二分图）：二分图存在完美匹配，当且仅当，对于所有左部点 \(S\) 都有 \(|nxt(S)|\geq |S|\)。
    • 推论：左部点集为 \(U\) 的二分图的最大匹配是 \(|U|-\max_{S\subseteq U}\{|S|-|N(S)|\}\)。枚举的 \(S\) 可以为空。
  • Kőnig 定理（二分图）：最小点覆盖 \(=\) 最大匹配数。
    • 方案：从左部每个非匹配点出发，再执行一次 dfs 寻找增广路的过程（一定会失败），标记访问过的节点。取左部未被标记的点、右部被标记的点，就得到了二分图最小点覆盖。
    • 推论：在二分图中，最大独立集 \(=\) 最小边覆盖 \(=\) \(n\) \(-\) 最小点覆盖 \(=\) \(n\) \(-\) 最大匹配。
  • DAG：最小路径覆盖 \(=\) \(n\) \(-\) 拆点二分图最大匹配。
  • DAG：最小链覆盖 \(=\) 传递闭包的最小路径覆盖。
  • Dilworth 定理（DAG）：最长反链 \(=\) 最小链覆盖。

欧拉回路

若存在欧拉回路，可使用以下算法找出一条欧拉回路：在全局维护当前的欧拉回路，dfs(u) 表示搜索到点 \(u\)，欲将求出欧拉回路，随意选择一个点开始 dfs。枚举一条还未访问的边 \((u, v)\)，然后 dfs(v)，然后将边 \((u, v)\) 插入欧拉回路的最前面。

匈牙利二分图匹配

bool dfs(int u) {
 if (vis[u] == tim) return 0;
 vis[u] = tim;
 for (int v: to[u]) 
  if (!mch[v] || dfs(mch[v]))
   return mch[v] = u, 1;
 return 0;
}
for (int i = 1; i <= n; i++) ++tim, ans += dfs(i);

网络流

最大流

最大流：Dinic 实现（version 5，ac-library style，完全 vector） 
template <class Cap>
struct mf_graph {
  struct edge {
    int v, rid;
    Cap cap;
  };
  int n;
  vector<vector<edge>> g;
  mf_graph() = default;
  mf_graph(int _n) : n(_n), g(_n) {}
  void addedge(int u, int v, Cap cap) {
    int fid = (int)g[u].size(), tid = (int)g[v].size() + (u == v);
    g[u].push_back({v, tid, cap});
    g[v].push_back({u, fid, 0});
  }
  vector<int> dep, cur;
  bool bfs(int s, int t) {
    dep.assign(n, -1);
    queue<int> q;
    dep[s] = 0;
    q.push(s);
    while (!q.empty()) {
      int u = q.front(); q.pop();
      for (auto&& e : g[u]) {
        if (e.cap && dep[e.v] == -1) {
          dep[e.v] = dep[u] + 1, q.push(e.v);
        }
      }
    }
    return dep[t] != -1;
  }
  Cap dfs(int u, Cap flw, int t) {
    if (u == t) return flw;
    Cap res = 0;
    for (int &i = cur[u]; i < (int)g[u].size(); i++) {
      auto &e = g[u][i];
      if (e.cap && dep[e.v] == dep[u] + 1) {
        Cap run = dfs(e.v, min(flw - res, e.cap), t);
        e.cap -= run, g[e.v][e.rid].cap += run;
        res += run;
        if (res == flw) return res;
      }
    }
    dep[u] = -1;
    return res;
  }
  Cap flow(int s, int t, Cap lim = numeric_limits<Cap>::max()) {
    Cap flw = 0;
    while (flw < lim && bfs(s, t)) {
      cur.assign(n, 0);
      flw += dfs(s, lim - flw, t);
    }
    return flw;
  }
};

费用流

注意看那个势能 \(h\) 的变化。

最小费用最大流：原始对偶 + dinic 实现（ac-library style，完全 vector） 
template <class T>
using pqueue = priority_queue<T, vector<T>, greater<T>>;
template <class Cap, class Cst>
struct mcf_graph {
  inline static constexpr auto MAXC = numeric_limits<Cst>::max();
  struct edge {
    int v, rid;
    Cap cap;
    Cst cst;
  };
  int n;
  vector<vector<edge>> g;
  mcf_graph() = default;
  mcf_graph(int _n) : n(_n), g(_n) {}
  void add(int u, int v, Cap cap, Cst cst) {
    int fid = (int)g[u].size(), tid = (int)g[v].size() + (u == v);
    g[u].push_back({v, tid, cap, cst});
    g[v].push_back({u, fid, 0, -cst});
  }
  vector<Cst> h, dis;
  vector<int> vis;
  bool spfa(int s) {
    vis.assign(n, false);
    h.assign(n, MAXC);
    vector<int> app(n, 0);
    queue<int> q;
    q.push(s), h[s] = 0;
    while (!q.empty()) {
      int u = q.front(); q.pop();
      vis[u] = false;
      for (auto&& e : g[u]) {
        if (e.cap && h[e.v] > h[u] + e.cst) {
          h[e.v] = h[u] + e.cst;
          if (!vis[e.v]) {
            if (++app[e.v] >= n) return false;
            vis[e.v] = true, q.push(e.v);
          }
        }
      }
    }
    return true;
  }
  bool dijkstra(int s, int t) {
    vis.assign(n, false);
    dis.assign(n, MAXC);
    pqueue<pair<Cst, int>> q;
    q.emplace(dis[s] = 0, s);
    while (!q.empty()) {
      int u = q.top().second; q.pop();
      if (exchange(vis[u], true)) continue;
      for (auto&& e : g[u]) {
        if (!e.cap) continue;
        auto w = e.cst + h[u] - h[e.v];
        if (dis[e.v] > dis[u] + w) q.emplace(dis[e.v] = dis[u] + w, e.v);
      }
    }
    return dis[t] != MAXC;
  }
  vector<int> cur;
  Cap dfs(int u, Cap flw, int t) {
    if (u == t) return flw;
    Cap res = 0;
    vis[u] = true; // dfs 不访问栈中节点
    for (int &i = cur[u]; i < (int)g[u].size(); i++) {
      auto &e = g[u][i];
      if (vis[e.v]) continue;
      if (e.cap && h[e.v] == h[u] + e.cst) {
        Cap run = dfs(e.v, min(flw - res, e.cap), t);
        e.cap -= run, g[e.v][e.rid].cap += run;
        res += run;
        if (res == flw) return vis[u] = false, res; // 退栈时如果流量流完了，可能会再次 dfs
      }
    }
    return res; // 退栈时如果流量流不完，那么将此点爆破
  }
  pair<Cap, Cst> flow(int s, int t, Cap lim = numeric_limits<Cap>::max()) {
    if (!spfa(s)) throw logic_error("sorry, cannot solve :(");
    Cap flw = 0;
    Cst sum = 0;
    while (flw < lim && dijkstra(s, t)) {
      for (int i = 0; i < n; i++) {
        if (dis[i] != MAXC) h[i] += dis[i];
      }
      cur.assign(n, 0);
      vis.assign(n, false);
      Cap run = dfs(s, lim - flw, t);
      flw += run, sum += run * h[t];
    }
    return make_pair(flw, sum);
  }
};

无源汇上下界可行流

这个图是无源汇的，那么可行流在这里指：每个点都流量平衡。

对于所有边 \(u\to v\) 带有 \([l,r]\) 的流量限制，使得 \(u\) 点强制流出 \(l\)，\(v\) 点强制流入 \(l\)，记录每个点的流入和流出，流入减流出记为 \(d_u\)。这个时候是不满足流量平衡的，拿出超级源汇 \(S,T\)，枚举点 \(u\)，如果 \(d_u>0\) 就是流入更多，连接 \(S\to u\) 流量为 \(d_u\) 的边；反之流出更多，连接 \(u\to T\) 流量为 \(-d_u\) 的边。

上面这一段原来写反了。主要是要知道这个 \(d_u\) 的流量差是我们想象出来的，我们连边是将想象变成现实。

将每条边的流量限制改为 \(r-l\)，并对所有边添加反向边（就正常反悔边），以 \(S\) 为源点，\(T\) 为汇点，跑最大流。如果 \(S\) 连出的点没有满流（由于 \(S,T\) 流量相等，\(T\) 流入的边也没有满流），则没有可行流；否则这就是一个可行流。

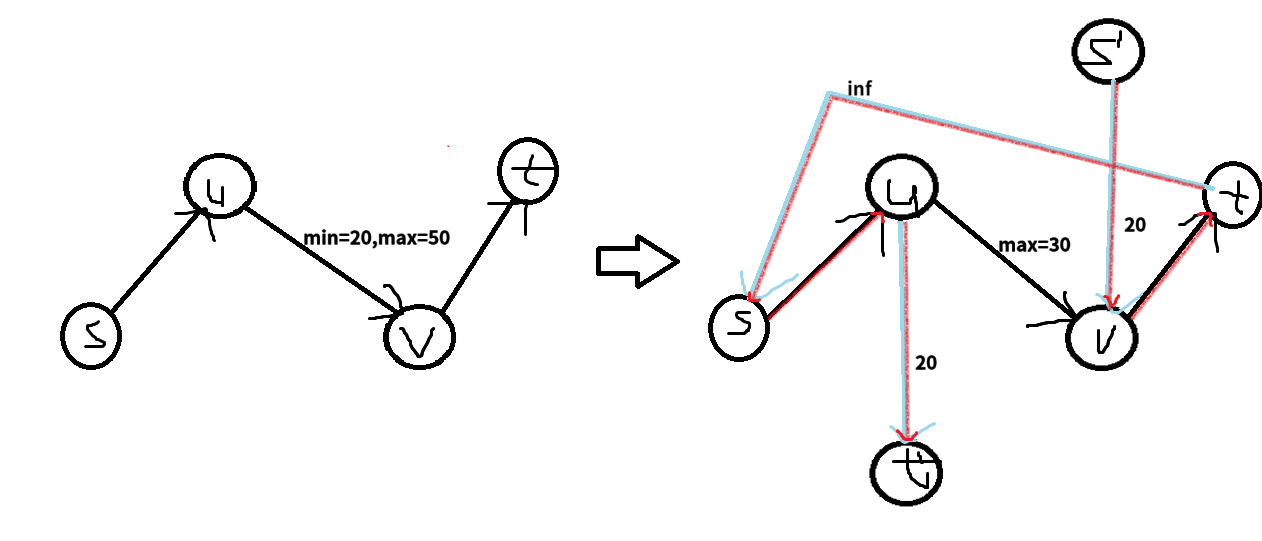
左边是原图，右边添加了 \(s', t'\) 的虚拟源点和浅蓝色的流量平衡边，以及红色的一条使 \(u\to v\) 流满 \(20\) 流量的流。

有源汇上下界可行流

  1. 设原图的源汇为 \(s,t\)。\(t\to s\) 连接容量 \(\infty\) 的边。
  2. 进行无源汇上下界可行流。

有源汇上下界最大/小流

  1. 跑一遍有源汇上下界可行流，如果没有就真的没有了，否则设可行流的流量为 \(flow_1\)。
  2. 删除 \(t\to s\) 的巨大无比的边。
  3. 删除 \(S,T\) 连出的流量平衡边（或者不用管，因为已经满流了）。
  4. 对于最大流，以 \(s\) 为源点，\(t\) 为汇点，在当前残量网络上跑最大流获得 \(flow_2\) 的流量，则答案为 \(flow1+flow_2\)。
  5. 对于最小流，以 \(t\) 为源点，\(s\) 为汇点，在当前残量网络上跑最大流获得 \(flow_2\) 的流量，则答案为 \(flow1-flow_2\)。

有负圈的费用流

给定一张 \(n\) 个点 \(m\) 条边的费用网络，源为 \(s\) 且汇为 \(t\)，求其最小费用最大流。

注意存在费用为负的边和总费用为负的环。

注意，本题中允许一个不经过 \(s,t\) 的环整体加上一个流量。事实上，若不允许这种情况的出现，则哈密顿路可以归约为这个问题。

对于一条费用为负的边 \((u, v, f, c)\)（\(f\) 为流量上界，\(c\) 为费用），将其改为一条强制满流的边 \((u, v, f, c)\)（并提前计算它的费用但不计算流量）和一条正常边 \((v, u, f, -c)\)（是原来边的反悔边）。其中，对于强制满流的那条边，使用上下界技术解决。但是在这里有一点不同，第一次跑的可行流得到的流量是强制满流的流量，但是实际上根据我们的建图实际含义，这些流量不是实打实流过去的，有一部分退回的流量通过反悔边送到虚拟汇点，这些流量需要被减去，第一次流的真实的流量应该是 \(t\) 到 \(s\) 的无穷边的流量。后面的事情都是一样的。

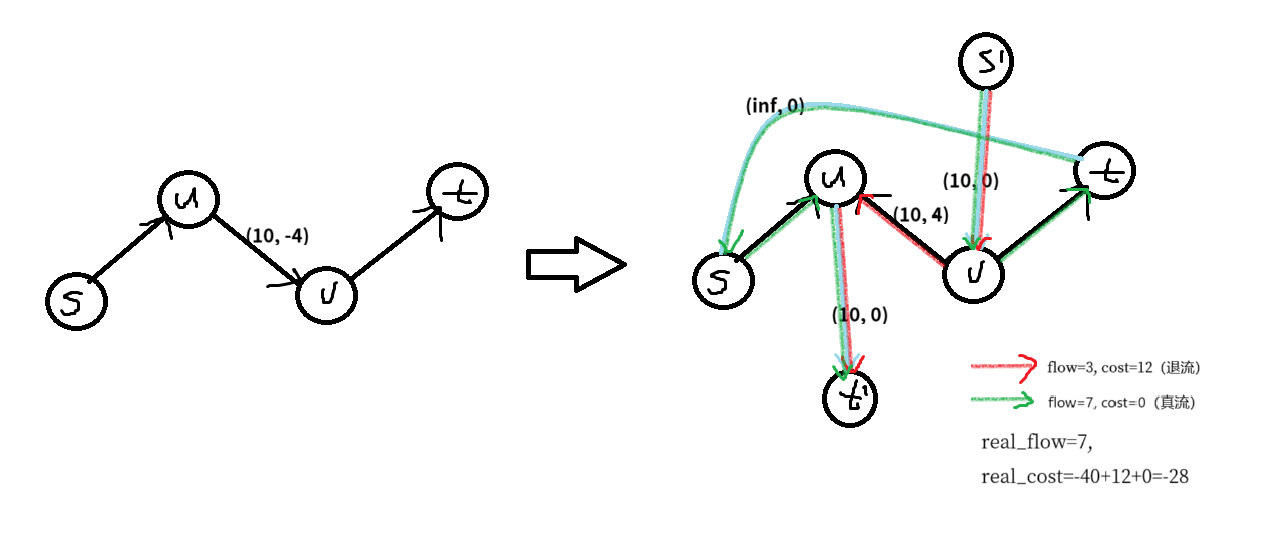
最小割

在网络图 \(G=(V,E)\) 中，割被定义为一种点集的划分方式：将所有的点划分成两个集合 \(s,t\)，满足 \(s\cup t=V,s\cap t=\varnothing,S\in s,T\in t\)。这个割的权值被定义为 \(\forall(u,v)\in E,u\in s,v\in t\) 的 \(w(u,v)\) 之和。

最大流-最小割定理：在任意网络中，最大流等于最小割。沿着残量网络从 \(S\) 找到的点就属于点集 \(s\)。

建图思路：若点 \(u\) 最终在 \(S\) 所能到达的点（即 \(s\) 集），点 \(v\) 最终在 \(S\) 所不能到达的点（即 \(t\) 集）时，将产生代价 \(w\)，则连边 \(u\to v\)，边权 \(w\)。

最大权闭合子图

我们说一个有向图是一张图的闭合子图，那么：

  • 它是一个有向图的子图；
  • 如果一个点在闭合子图中，它在原图中的所有出边指向的点都在这张新的闭合子图中。

那么最大权闭合子图就是权值和最大的子图。

建图方法：正权点连 \(S\)，负权点（点权取反后）连 \(T\)，其他边保留为无穷大，答案是正权点之和 - 最小割。所选的点集是 \(s\) 集。

平面图最小割定理

平面图是一个图，若存在某种在平面上画出图的方式，使得边与边只在顶点相交的图，被称为平面图。

对于一个平面图，都有其对应的对偶图：

  • 平面图被划分出的每一个区域当作对偶图的一个点；
  • 平面图中的每一条边两边的区域对应的点用边相连，特别地，若两边为同一区域则加一条回边（自环）。

这样构成的图即为原平面图的对偶图。

有定理：平面图最小割等于对偶图最短路。

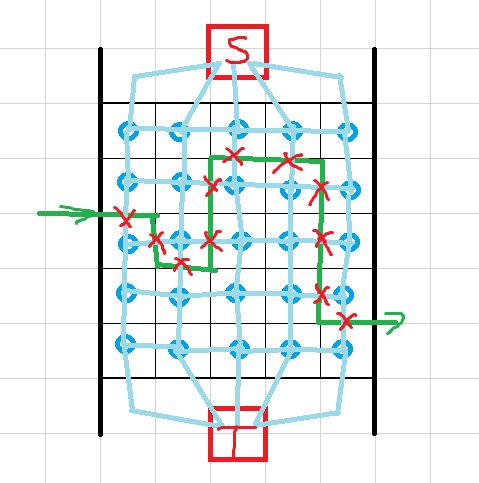
平面图欧拉定理

\(V\) 个点，\(E\) 条边，\(F\) 个面（如果是平面图则要算上外面的无穷大的面），\(B\) 个连通块的平面图，满足 \(V-E+F=B+1\)。

树论

右链法求虚树

void buildVTree(vector<int> h) {
  static int vis[1 << 18], tim = 0, stk[1 << 18];
  if (h.empty()) return;
  ++tim;
  sort(h.begin(), h.end(), [&](int u, int v) { return dfn[u] < dfn[v]; });
  bool flag = 0;
  if (h[0] != 1)
    h.insert(h.begin(), 1);
  else
    flag = 1;
  h.erase(unique(h.begin(), h.end()), h.end());
  auto link = [&](int u, int v) {
    if (vis[u] < tim) vis[u] = tim, t[u].clear();
    if (vis[v] < tim) vis[v] = tim, t[v].clear();
    t[u].emplace_back(v, getDist(u, v));
    t[v].emplace_back(u, getDist(u, v));
  };
  int top = 0;
  stk[++top] = h[0];
  for (int i = 1; i < h.size(); i++) {
    int k = getLca(stk[top], h[i]);
    if (k != stk[top]) {
      while (top >= 2 && dfn[stk[top - 1]] > dfn[k])
        link(stk[top - 1], stk[top]), --top;
      if (stk[top - 1] == k)
        link(stk[top], k), --top;
      else
        link(stk[top], k), stk[top] = k;
    }
    stk[++top] = h[i];
  }
  while (top >= 3) link(stk[top - 1], stk[top]), --top;
  if (top >= 2 && (flag || vis[1] == tim)) link(stk[top - 1], stk[top]);
}

二次排序求虚树

void build(int h[], int m) {
  t.tag++, t.cnt = 0;
  for (int i = 1; i <= m; i++) vis[h[i]] = t.tag;
  auto link = [&](int u, int v) { if (dep[u] < dep[v]) swap(u, v); t.link(u, v, query(u, dep[u] - dep[v])); };
  h[++m] = 1;
  sort(h + 1, h + m + 1, [&](int i, int j) { return dfn[i] < dfn[j]; });
  for (int i = 1; i < m; i++) h[m + i] = lca(h[i], h[i + 1]);
  m += m - 1;
  sort(h + 1, h + m + 1, [&](int i, int j) { return dfn[i] < dfn[j]; });
  m = unique(h + 1, h + m + 1) - h - 1;
  for (int i = 2; i <= m; i++) link(h[i], lca(h[i], h[i - 1]));
}

dfn 序求 LCA

int n, m, dfn[100010], ST[20][100010], dep[100010], rnk[100010], cnt;
basic_string<int> g[100010];
bool cmp(int u, int v) { return dfn[u] < dfn[v]; }
void dfs(int u, int fa) {
  dfn[u] = ++cnt, rnk[cnt] = u, ST[0][cnt] = fa, dep[u] = dep[fa] + 1;
  for (int v : g[u]) if (v != fa) dfs(v, u);
}
int lca(int u, int v) {
  if (u == v) return u;
  auto [l, r] = minmax(dfn[u], dfn[v]);
  int k = 31 - __builtin_clz(r - l);
  return min(ST[k][l + 1], ST[k][r - (1 << k) + 1], cmp);
}
int main() {
  cin >> n >> m;
  for (int i = 1, u, v; i < n; i++) cin >> u >> v, g[u] += v, g[v] += u;
  dfs(1, 0);
  for (int j = 1; 1 << j <= n; j++) {
    for (int i = 1; i + (1 << j) - 1 <= n; i++) {
      ST[j][i] = min(ST[j - 1][i], ST[j - 1][i + (1 << (j - 1))], cmp);
    }
  }
  // ...
}

prufer 序列

给定一棵 \(n\) 个点的无根树，每次选择一个编号最小的叶节点并删掉它，然后在序列中记录下它连接到的那个节点。最终剩余两个点停止算法，得到一个 \(n-2\) 长的值域 \([1, n]\) 的序列称作 prufer 序列。

根据 prufer 序列的性质，我们可以得到原树上每个点的度数。每次我们选择一个编号最小的度数为 \(1\) 的节点，与当前枚举到的 prufer 序列的点连接，然后同时减掉两个点的度数。重复 \(n-2\) 次后就只剩下两个度数为 \(1\) 的节点，其中一个是 \(n\)，把它们连接起来即可。

一个 prufer 序列与一棵有标号无根树形成双射。这导出 Cayley 定理：\(n\) 个点的无向完全图有 \(n^{n-2}\) 个生成树。

数学

排列与置换环

  • 对所有 \(i\) 在新的有向图中 \(i\to p_i\) 连边，形成若干单点或有向环，称为排列的置换环分解。

  • 置换环的开根 see 题解 CF1787F，就是尝试还原置换环形态，跳着填数。

  • 置换环的幂：对于长度为 \(n\) 的置换环 \(A\)，\(A^k\) 是 \(\gcd(n,k)\) 个长度相等的置换环的和。

  • 排列的置换环个数期望是调和级数。

  • 排列的康托展开 \(rank=\sum_{i=1}^ns_i(n-i)!\) where \(s_i=\sum_{j>i}[p_j<p_i]\)。

  • 允许任意交换排列中的两个元素，那么使其单调递增的最小步数为 \(n\ -\) 置换环个数。

  • 允许任意交换排列中的两个元素，那么使其单调递增的最小步数的方案数为 \(\binom{n-|cycs|}{c_1-1, c_2-1, \cdots, c_{|cycs|}-1}\prod_{c\in cycs}c^{c-2}\)。

反射容斥

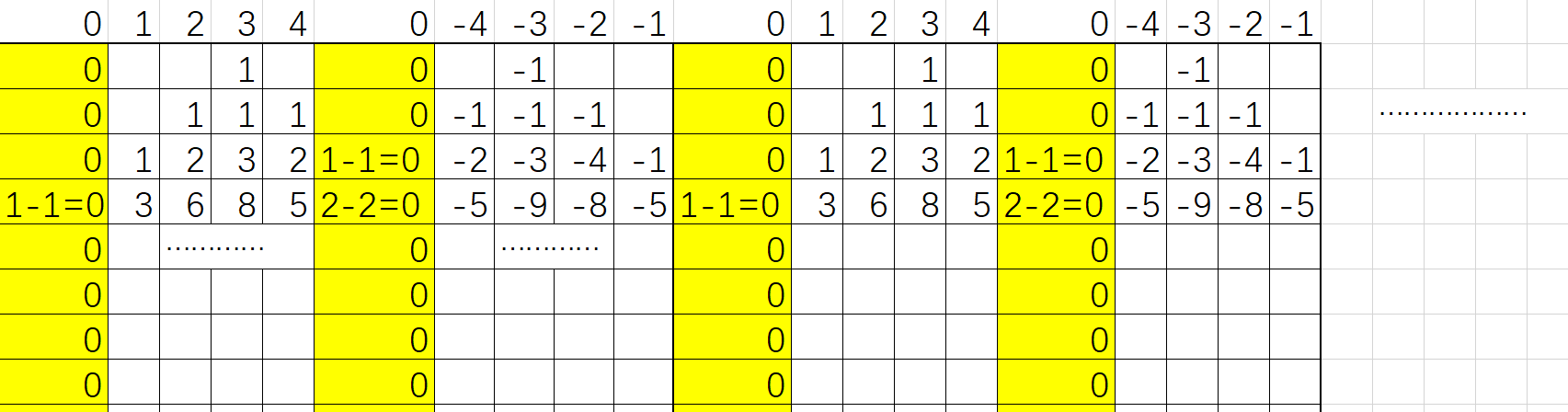
从坐标 \((0, s)\to(m, t)\)，中间每一步需要保证 \(0\leq y\leq n\)，每一步走右上或者右下。求方案数。

根据上文 1D 部分的题解，直接刻画答案为

\[[x^t] (x^s-x^{-2-s})(x+1/x)^m=[x^t] \sum_{i=0}^m \binom m i x^{2i-m+s}-[x^t]\sum_{i=0}^m \binom m i x^{2i-m-2-s}\pmod {x^{2n+4}-1} \]

也就是需要回答

\[solve(m, v, p)=\sum_{i=0}^m \binom m i [2i\equiv v\pmod p] \]

的问题，答案为

\[solve(m, m - s+t, 2n+4)-solve(m, m+s+2+t, 2n+4) \]

可能变动的部分为 \((x+1/x)\) 这个部分，可以改，改完以后还是二项式定理拆一下，化为 \(solve\) 解决的形式。大道至简。

二项式系数恒等式

名称 公式 限制
阶乘展开式 \(\displaystyle\binom n k=\frac{n!}{k!(n-k)!}\) 整数 \(n\geq k\geq 0\)
对称恒等式 \(\displaystyle\binom n k=\binom n {n-k}\) 整数 \(n\geq 0\)，\(k\) 为整数
吸收/提取恒等式 \(\displaystyle\binom n k=\frac{n}{k}\binom{n-1}{k-1}\) 整数 \(k\neq 0\)
加法/归纳恒等式 \(\displaystyle\binom n k=\binom{n-1}{k}+\binom{n-1}{k-1}\) \(k\) 为整数
上指标反转 \(\displaystyle\binom {-n} k=(-1)^k\binom{n+k-1}{k}\) \(k\) 为整数
三项式版恒等式 \(\displaystyle\binom n m\binom m k=\binom n k\binom{n-k}{m-k}\) \(m,k\) 为整数
二项式定理 \(\displaystyle\sum_k\binom n k x^k y^{n-k}=(x+y)^n\) 右式收敛
平行求和法 \(\displaystyle\sum_{k\leq m}\binom{k+n}{k}=\binom{n+m+1}{m}\) \(n\) 为整数
上指标求和 \(\displaystyle\sum_{0\leq k\leq n}\binom k m=\binom{n+1}{m+1}\) 整数 \(n,m\geq 0\)
范德蒙德卷积 \(\displaystyle\sum_k \binom r k\binom{s}{n-k}=\binom{r+s}{n}\) \(n\) 为整数
补充：三项式系数 \(\displaystyle\binom{n+m+k}{n,m,k}=\frac{(n+m+k)!}{n!\ m!\ k!}\) \(n, m, k\) 为非负整数

注：二项式定理的完整适用条件为：整数 \(n\geq 0\) 或 \(\text{abs}(x/y)<1\)。

吸收恒等式等价写法：\(\displaystyle\binom n k=\frac{k+1}{n+1}\binom{n+1}{k+1}\)。

二项式反演

基本来源

\[\begin{aligned} |S_1\cup S_2\cup\cdots\cup S_n|=\sum_{T\subseteq\{1,2,\cdots,n\}}(-1)^{|T|+1}|S_{T_1}\cap S_{T_2}\cap\cdots\cap S_{T_{|T|}}| \end{aligned} \]

子集容斥

\[g(S)=\sum_{S\subseteq T}f(T)\iff f(T)=\sum_{T\subseteq S}g(S)\cdot(-1)^{|S|-|T|} \]

\[g(S)=\sum_{T\subseteq S}f(T)\iff f(T)=\sum_{S\subseteq T}g(S)\cdot(-1)^{|T|-|S|} \]

钦定容斥

\[g(k)=\sum_{k\leq i\leq n}\binom{i}{k}f(i)\iff f(k)=\sum_{k\leq i\leq n}(-1)^{i-k}\binom{i}{k}g(i) \]

\[g(k)=\sum_{m\leq i\leq k}\binom{k}{i}f(i)\iff f(k)=\sum_{m\leq i\leq k}(-1)^{k-i}\binom{k}{i}g(i) \]

\(f(t)\) 是所有的恰好满足 \(t\) 个条件的方案数，\(g(t)\) 是钦定了任意 \(t\) 个条件后的方案数的和，对于每一个方案他会重复数 \(\binom{|S|}{t}\) 次！

溢出容斥

求出 \(h(n,m,k)\)：将 \(n\) 个相同的小球放入 \(m\) 个互不相同的盒子里，要求每个盒子最少 \(0\) 个最多 \(k\) 个的方案数。

  • 辅助 \(g(n,m)\)：将 \(n\) 个相同的小球放入 \(m\) 个互不相同的盒子里，要求每个盒子最少 \(0\) 个（去掉上限）的方案数，明显 \(g(n,m)=\binom{n+m-1}{m-1}\)。
  • 容斥。考虑钦定 \(i\) 个盒子溢出了，将这些盒子的球数减去 \((k+1)\)。现在数一下：\(\Delta=i(k+1),ans=g(n-\Delta,m)\)。
  • 盲猜容斥系数为 \((-1)^i\binom{m}{i}\)，所以 \(h(n,m,k)=\sum_{0\leq i\leq m} (-1)^i\binom{m}{i}g(n-\Delta,m)\)。

DAG 容斥

一个有向图有 \(n\) 个点，求它的 DAG 子图数量。\(n\leq 15\)。

令 \(f[S]\) 表示点集 \(S\) 有多少个 DAG 子图。枚举这个 DAG 中入度为 0 的部分，然后递归下去。

\[f[S]=\sum_{T\subseteq S,T\neq\varnothing}2^{ways(T,S-T)}f[S-T] \]

由于不能一次枚举完所有入度为 0 的点，同一种方案会算重，我们对着这些点容斥。

\[f[S]=\sum_{T\subseteq S,T\neq\varnothing}(-1)^{|T|+1}2^{ways(T,S-T)}f[S-T] \]

博弈论

必胜必败态

定义 必胜状态 为 先手必胜的状态，必败状态 为 先手必败的状态。

通过推理，我们可以得出下面三条定理：

  • 定理 1：没有后继状态的状态是必败状态。
  • 定理 2：一个状态是必胜状态当且仅当存在至少一个必败状态为它的后继状态。
  • 定理 3：一个状态是必败状态当且仅当它的所有后继状态均为必胜状态。

SG 定理

对于状态 \(x\) 的 \(k\) 个后继状态 \(y_1, \cdots, y_k\)，定义

\[SG(x)=\operatorname{mex}\limits_{i=1}^k\{SG(y_i)\} \]

显然无后继状态的先手必败态的 SG 为 \(0\)，与之相反的是 SG 不为 \(0\) 则先手必胜。对于多个有向图游戏组成的大游戏（名字乱起的），这个大游戏的 SG 值为所有有向图游戏的起点的 SG 值的异或。注意啥叫大游戏，每次每人选其中一个游戏进行操作可以组成大游戏。

nim 游戏是一个大游戏，每堆石子构成一个有向图游戏。当某堆石子有 \(x\) 个时，\(SG(x)=x\)。

凸优化

斜率优化

直线 \(y=kx+b\)，随着 \(b\) 向上，碰到的第一个点就是决策点，因此将决策点写成 \((x, y)\) 使答案为 \(b=y-kx\)。

四边形不等式

四边形不等式：交叉小于包含。\(l_1<l_2<r_1<r_2\to w(l_1,r_1)+w(l_2,r_2)\leq w(l_1,r_2)+w(l_2,r_1)\)。

区间包含单调性：包含区间值单调。\(l_1<l_2<r_2<l_1\to w(l_1,r_1)\geq w(l_2,r_2)\)。

满足四边性不等式的 \(w\)，在外面套一个凸函数（一阶导数单调增加的函数，例如平方），还是四边形不等式。

若有 \(w(l,r)=f(r)-g(l)\)，则满足四边形恒等式。

2D/1D 暴力决策单调性

\(opt(i,j)\) 表示 \(f(i,j)\) 从哪个 \(k\) 转移得到。\(opt(i,j-1)\leq opt(i,j)\leq opt(i+1,j)\)。为什么这样？考虑在平面直角坐标系中画出来这些点，状态黑点对应决策红点，画出来是一行斜线，总转移量是 \(O(n)\) 的，最后均摊 \(O(n^2)\)。做的时候使 \(opt(i,j)\) 在 \(opt(i,j-1)\) 到 \(opt(i+1,j)\) 枚举，复杂度分析时一个点会被加一次和减一次，剩下的不超过 \(O(n^2)\)。

划分段问题

结论：满足四边形不等式的 \(w\)，有性质，\(n\) 个物品划分成 \(k\) 段，与划分成 \(k-1\) 段的方案是交错的。在环上时（换起点）也是如此，就是决策点在每个区间中选个点。

WQS 二分

WQS 二分本质上就是用斜率 \(k\) 切凸包，假设切了 \((x,y)\)，算出来 \(y-kx\)，这个 \(kx\) 就是多的贡献，于是可以还原真实值。通过判断 \(x\) 与目标 \(K\) 的关系，不断调整斜率最终切到答案。

  • 做 \(g\) 的 DP 时，额外记录 \(g\) 取最小值时用了多少个邮局（记录方案，而不是记录在状态中），这样就知道最后切到的 \(x\) 在哪里。

  • 有一个边界问题，最后切了很多个点共线，有一种方法是记录切到最小的 \(x_1\)，直到找到最大的 \(x_1\) 满足 \(x_1\leq m\)，用它来更新答案。

  • 为什么答案一定是整数？1. \(f(x)\) 为整数 2. \(x\) 的定义域为整数 3. 答案的斜率是两个相邻点连接的线的斜率。所以答案的斜率为整数，即 \(\frac{f(K)-f(K-1)}{1}\)。同时斜率上界为 \(f(x)\) 的上界。

1D/1D 队列维护决策单调性

1D/1D 的 DP 中，维护队列 \((l,r,j)\) 表示 \(f_{i\in[l,r]}\) 都应该由 \(f_j\) 转移而来，\(j\leq l\)。队列中 \(j\) 单调，\([l,r]\) 顺次相连。

  1. 欲求 \(f_i\)，那么检查队头 \(r_h<i\) 的 \((l_h,r_h,j_h)\) 的删掉。取出队头进行转移。\(l_h=i\)。
  2. 试图插入决策 \(i\) 的时候：
    1. 记队尾为 \((l_t,r_t,j_t)\)。
    2. 如果对于 \(f[l_t]\) 来说，\(i\) 优于 \(j_t\)，删除队尾，\(pos=l_t\)，返回第一步。
    3. 如果对于 \(f[r_t]\) 来说，\(j_t\) 优于 \(i\)，\(pos=r_t+1\)，去往第五步。
    4. 在 \([l_t,r_t]\) 中二分一个 \(pos\)，使得 \(pos\) 往后是 \(i\) 更优，往前是 \(j_t\) 更优，去往第五步。
    5. 插入决策 \((pos,n,i)\)。

这样的总复杂度为 \(O(n\log n)\)。

2D/1D 分治维护决策单调性

考虑分治：假如我们已经有划分成 \(d-1\) 段的答案，欲求所有的 \(f_{i,d}\)。考虑欲求 \(f_{[L,R],d}\)，现在有效的决策集合是 \([l,r]\)。我们求出 \(f_{mid,d}\) 的值：用 \([l,r]\) 的决策更新。假如找到一个最优决策在 \(p\)。那么我们断定：\([L,mid)\) 的点的决策为 \([l,p]\)，\((mid,R]\) 的点的决策为 \([p,r]\)。

分析复杂度：一共 \(O(\log n)\) 层，每层平摊 \(O(n)\)。我们的 \(V(l,r)\) 的复杂度如何分析？考虑左右指针是独立的；考虑对于一个指针，在分治树上的每一个点恰好踩过一次，所以移动量为 \(O(n\log n)\)。所以总复杂度为 \(O(n\log^2 n)\)。

线性规划

对偶定理

设：（记 \(\mathbf A\) 为向量，\(\mathbf A^T\) 是 \(\mathbf A\) 的转置）

  • \(\mathbf x\) 是一个 \(n\times 1\) 的列向量。
  • \(\mathbf c\) 是一个 \(n\times 1\) 的列向量。
  • \(A\) 是一个 \(m\times n\) 的矩阵。
  • \(\mathbf b\) 是一个 \(m\times 1\) 的列向量。

则原问题为：

\[\begin{aligned} &\text{minimize}& \mathbf c^T\mathbf x\\ &\text{s.t.}& A\mathbf x\geq \mathbf b,\mathbf x\geq 0 \end{aligned} \]

其中 \(\mathbf x\geq 0\) 表示 \(\forall x_i\geq 0\)。

这个问题的对偶问题是：

\[\begin{aligned} &\text{maximize}& \mathbf b^T\mathbf y\\ &\text{s.t.}& A^T\mathbf y\leq \mathbf c,\mathbf y\geq 0 \end{aligned} \]

其中 \(\mathbf y\) 是我们新加的 \(m\times 1\) 的未知列向量。

（如果你无法理解，就尝试用矩阵的维数乘一下看看乘出来是什么。\(\mathbf c^T\mathbf x\) 实际上是向量 \(\mathbf c,\mathbf x\) 内积。）

弱对偶定理：\(\mathbf c^T\mathbf x\) 的任意一组解 \(\geq \mathbf b^T\mathbf y\)。

强对偶定理：\(\min \mathbf c^T\mathbf x=\max \mathbf b^T\mathbf y\)。

（注意 \(\min\) 配 \(\geq\)，\(\max\) 配 \(\leq\)）

最大费用循环流对偶

https://notes.sshwy.name/Math/Linear-Algbra/LP-and-its-Dual/#简化对偶问题-1

看到这里了就再看一下吧（其实根本不会）。

posted @ 2025-11-08 13:28  caijianhong  阅读(36)  评论(0)    收藏  举报