题解：QOJ9282 [Moscow21B] Gleb and Liteyny Avenue / ZROI3204 [25noi-day7] 银河楼酒店

题解：QOJ9282 [Moscow21B] Gleb and Liteyny Avenue / ZROI3204 [25noi-day7] 银河楼酒店

题目描述

一条长为 \(L=10^{100}\) 的马路，你在坐标为 \(0\) 的马路左侧，要去到坐标为 \(L\) 的马路右侧的银河楼酒店。一路上顺次有 \(n\) 条斑马线，第 \(i\) 条坐落在坐标 \(x_i\) 处。所有斑马线都配有红绿灯，每个红绿灯都是以 \(g\) 秒绿灯，\(r\) 秒红灯为周期进行循环。过马路要 \(b\) 秒，要求这期间都是绿灯。这座城市的设计是合理的，所以不会出现过于密集的斑马线。具体的，对于所有 \(i\) 有 \(x_{i+2}-x_i > r+g\) 。

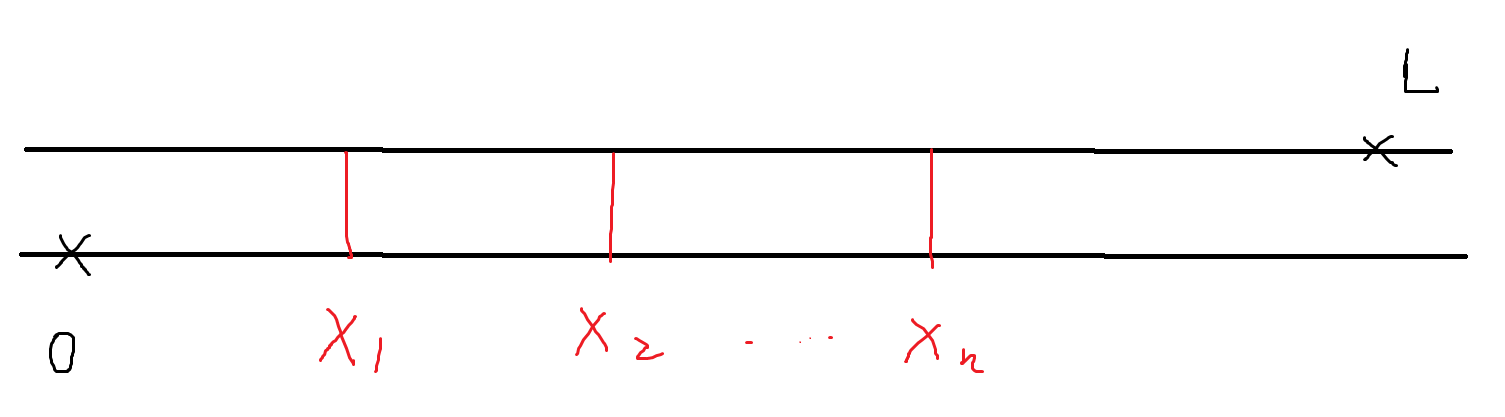
问题是红绿灯不一定是同步的。具体的，每个红绿灯都有一个均匀随机的整数偏移量 \(x\in[0,g+r-1]\) 代表其偏移的时间。你不知道每个红绿灯的偏移量。当你走到 \(x_i\) 时，你可以看到 \(i\) 这个红绿灯上的数字（还有多少秒切换颜色）。你的移动速度是 \(1\) 单位每秒，且你可以往上下两个方向移动。你想尽快到达终点，所以你希望最小化期望到达时间。

显然你至少要移动 \(L\) 秒，所以请输出期望时间减去 \(L\) 的结果。

（对于到达过的红绿灯，你可以知道其偏移量。对于未到达过的红绿灯，你认为其偏移量是均匀随机的。）

数据范围大概是 \(n\leq 10^6, g+r\leq 10^9\)。

题解

\(L, b\) 都是没用的，我们只关心过马路之前额外花费了多少秒。然后因为过马路的时候要一直路灯，实际上能过的秒数也就 \(G=g-b+1\) 秒，剩下 \(R=r+b-1\) 秒都是过不了的，这就是一个简单的转化。再额外令 \(T=R+G\)。

为什么这个题可以做呢，如果这个人要记住前面出现过的所有红绿灯的周期，还要决策，那就很难做。但是发现

1. 答案不超过 \(R\)。因为可以直接等 \(R\) 秒然后过马路。
2. 又因为 \(x_{i+2}-x_i > r+g\)，所以一旦回头超过两个红绿灯，答案就一定超过 \(R\) 了。

这样就可以先写一个和 \(R+G\) 有关的 dp。令 \(dp_{i,j}\) 表示在第 \(i\) 个灯，此时距离绿灯还有 \(j\) 秒，不回头，最小期望步数。

\[dp_{i,j}=\min\left(j, \frac1T\sum_{k=1}^R\min(w(j, d), dp_{i+1,k})\right) \]

其中 \(d=2(x_{i+1}-x_i)\)，\(w(j,d)\) 函数计算从 \(i+1\) 走到 \(i\) 走的路程和要继续等的时间。注意，这个 \(w(j,d)\) 应该是分三段的一次函数：本来是应该先计算 \(j'=(j-d)\bmod T\)，如果 \(j'>R\) 则返回 \(d\)，否则返回 \(d+j'\)。但是发现这样答案要么是 \(d\)，要么是 \(j+kT-d+d\)，注意到如果 \(k>0\)，我们可以直接视作 \(w\) 返回的是无穷大，因为和它在一个 \(\min\) 中的 \(dp_{i+1,k}\) 不超过 \(T\)，而 \(w\) 计算出来超过 \(T\) 了，这就是优化的关键。我们可以仔细写一下这个 \(w\)：

\[w(j,d)=\begin{cases} j, &d\leq j\\ d,&d-G<j<d\\ \infty, &j\leq d-G \end{cases} \]

至此可以获得一点点分数，为了继续优化，需要注意到：\(x_{i+1}-x_i<R/2\) 与 \(x_{i+2}-x_{i+1}<R/2\) 不能同时发生，这导致它们其中的一个一定不会回头。

我们改进计算，如果 \(x_{i+1}-x_i<R/2\)，那么

\[dp_{i,j}=\min\left(j, \frac1T\sum_{k=1}^R\min\left(w(j, d), \min\left(k, \frac1T\sum_{t=1}^R dp_{i+2,t}\right)\right)\right) \]

\(d\) 仍然为 \(2(x_{i+1}-x_i)\)。这里就会少掉一个决策，有优化的可能了。

我们令 \(S_i=\frac1T\sum_{j=1}^Rdp_{i,j}\)，则如果 \(x_{i+1}-x_i<R/2\)，那么

\[S_i=\frac1T\sum_{j=1}^R\min\left(j, \frac1T\sum_{k=1}^R\min\left(w(j, d), k, S_{i+2}\right)\right) \]

对 \(w(j,d)\) 取值进行拆分，其取 \(j\) 时：

\[\frac1T\sum_{j=?}^?\min\left(j, \frac1T\sum_{k=1}^R\min\left(j, k, S_{i+2}\right)\right) \]

发现第一个 \(\min\) 的那个 \(j\) 是没有用的，因为后面的显然 \(<j\) 了。那就是要求

\[\frac1{T^2}\sum_{j=?}^?\sum_{k=1}^R\min\left(j, k, S_{i+2}\right) \]

枚举 \(t=\min(i,j)\) 计算有多少对 \(i, j\) 取到这个值，发现只和 \(t\) 有关，然后再分类 \(t<S_{i+2}\) 和 \(t\geq S_{i+2}\) 的情况，需要求 \(x^2\) 的前缀和。

\[\sum_{i=1}^ni^2=\frac{n(n+1)(2n+1)}6 \]

\(w(j,d)=d\) 时：

\[\frac1T\sum_{j=?}^?\min\left(j, \frac1T\sum_{k=1}^R\min\left(d, k, S_{i+2}\right)\right) \]

其实就是要求 \(\sum_{i=?}^?\min(i,x)\) 套两次娃。这个式子比上面那个更好做。

\(w(j,d)=\infty\) 时和上一个一样是套两次娃。

至此就做完了，复杂度 \(O(n)\)。

总结

需要想到只会回头一个红绿灯，又想到每两段只有一段可能回头，从而将答案写成 \(O(n)\) 次 \(x=f(x)\) 的操作，发现 \(w(j,d)\) 只用分三段，分讨 \(w\) 取值把 \(f(x)\) 逐步化简，把它做到 \(O(1)\) 就做完了。

代码

#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define endl "\n"
#define debug(...) void(0)
#endif
using LL = long long;
constexpr int N = 5e5 + 10;
template <class T> T& chkmin(T& x, const T& y) { if (x > y) x = y; return x; }
template <class T> T& chkmax(T& x, const T& y) { if (x < y) x = y; return x; }
int R, G, B, n, T, L;
LL a[N];
double S[N];
LL calc(int j, LL d) {
  j = (j - d % T + T) % T;
  return (j > R ? 0 : j) + d;
}
double sum(LL lim, double val) {
  // sum_{j=1..lim} min(j, val)
  if (val <= 0) return val * lim;
  auto p = min((LL)val, lim);
  return 1.0 * p * (p + 1) / 2 + val * (lim - p);
}
double sum_range(LL l, LL r, double val) {
  // sum_{j=l..r} min(j, val)
  return sum(r, val) - sum(max(l - 1, 0ll), val);
}
double check(double val) {
  return sum(R, val) / T;
}
template <int k> __int128 presum(LL n);
template <> __int128 presum<0>(LL n) { return n + 1; }
template <> __int128 presum<1>(LL n) { return n * (n + 1) / 2; }
template <> __int128 presum<2>(LL n) { return 1.0 * n * (n + 1) * (2 * n + 1) / 6; }
template <int k> __int128 rangesum(LL l, LL r) { return presum<k>(r) - presum<k>(l - 1); }
auto rangesum2(LL l, LL r, LL a) { return l > r ? 0 : a * rangesum<0>(l, r); }
auto rangesum2(LL l, LL r, LL a, LL b) { return l > r ? 0 : a * rangesum<1>(l, r) + b * rangesum<0>(l, r); }
auto rangesum2(LL l, LL r, LL a, LL b, LL c) { return l > r ? 0 : a * rangesum<2>(l, r) + b * rangesum<1>(l, r) + c * rangesum<0>(l, r); }
double qwqdxw(int n, int m, double val) {
  // sum_{i=1}^n sum_{j=1}^m min(i, j, val)
  int p = min((int)val, min(n, m));
  LL A = (LL)n + m + 1;
  return rangesum2(1, p, -2, A, 0) + rangesum2(p + 1, min(n, m), -2, A) * val;
}
int mian() {
  cin >> n >> L >> G >> R >> B;
  tie(G, R) = make_pair(G - B + 1, R + B - 1);
  debug("R = %d\n", R);
  T = R + G;
  for (int i = 1; i <= n; i++) cin >> a[i];
  S[n + 1] = 2e9;
  for (int i = n; i >= 1; i--) {
    if (i == n || a[i + 1] - a[i] >= (R + 1) / 2) {
      S[i] = check(S[i + 1]);
    } else {
      LL d = 2 * (a[i + 1] - a[i]);
//    for (int j = 1; j <= R; j++) {
//      S[i] += min((double)j, check(min(S[i + 2], (double)calc(j, d))));
//    }
      // [d, R]
      if (d <= R) {
//      for (int j = (int)d; j <= R; j++) S[i] += min((double)j, check(min(S[i + 2], (double)j)));
//      for (int j = (int)d; j <= R; j++) S[i] += check(min(S[i + 2], (double)j));
        S[i] += (qwqdxw(R, R, S[i + 2]) - qwqdxw(d - 1, R, S[i + 2])) / T;
      }
      LL l = max(d - G + 1, 1ll), r = min(d - 1, (LL)R);
      if (l <= r) {
        S[i] += sum_range(l, r, check(min(S[i + 2], (double)d)));
//      for (int j = (int)l; j <= (int)r; j++) S[i] += min((double)j, check(min(S[i + 2], (double)d)));
      }
      if (d - G >= 1) {
        S[i] += sum_range(1, d - G, check(S[i + 2]));
//      for (int j = 1; j <= (int)(d - G); j++) S[i] += min((double)j, check(S[i + 2]));
      }
      S[i] /= T;
    }
    debug("S[%d] = %.4lf\n", i, S[i]);
  }
  cout << fixed << setprecision(16) << L + B + S[1] << endl;
  return 0;
}
int main() {
#ifndef LOCAL
  cin.tie(nullptr)->sync_with_stdio(false);
#endif
  int t = 1;
  //cin >> t;
  while (t--) mian();
  return 0;
}