题解：CF1019E Raining season / 【模板】半平面交对偶

题解：CF1019E Raining season

可以将这题作为半平面交模板题，虽然很奇怪。

题目描述

给出一棵树，每条边的边权是一个一次函数 \(a_i​x+b_i\) ​，求当 \(x=0,1,⋯m−1\) 时树的直径。

\(n\leq 10^5, m\leq 10^6, a_i, b_i\geq 0\)。

点 - 线对偶

平面上的点 \((p,q)\) 的对偶直线为 \(y=px-q\)，直线 \(y=px-q\) 的对偶点为 \((p,q)\)。这样的对偶叫做点 - 线对偶。

点 - 线对偶有一些优良的性质。

1. 对偶性：点 \(P\) 在直线 \(l\) 上，当且仅当点 \(p\) 对偶的直线经过直线 \(l\) 对偶的点。
2. 顺序保持：点 \(P\) 在直线 \(l\) 上方，当且仅当对偶直线在对偶点下方。
3. 凸包与半平面交的对偶关系：半平面交对应对偶空间中的凸包顶点，反之亦然。

举一个例子，原平面上直线 \(y=-x+5\) 与 \(y=2x+2\) 交于点 \((1,4)\)，将以上提到的三个东西分别对偶得到：过点 \((-1,-5)\) 与点 \((2,-2)\) 的直线为 \(y=x-4\)。

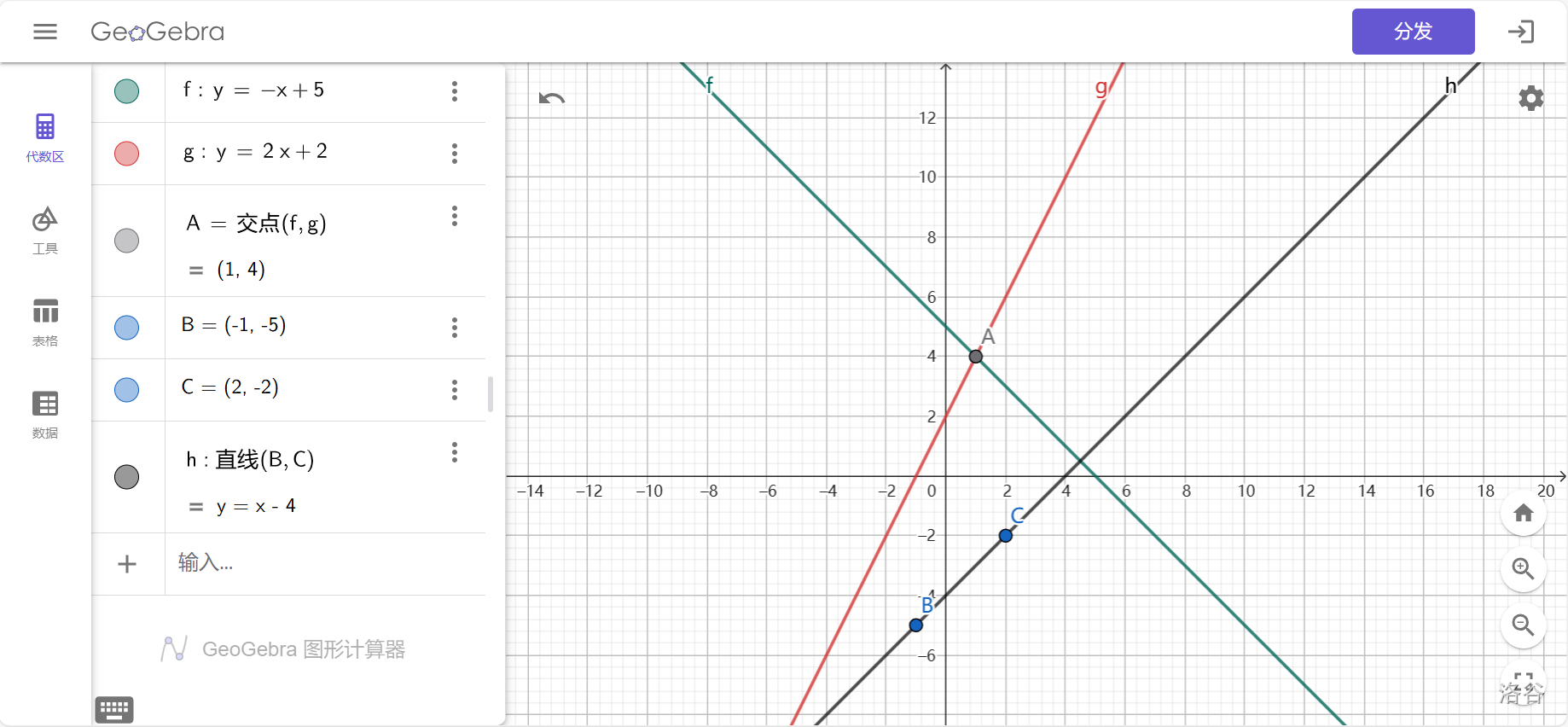
可以自行改别的参数玩一下。

题解

首先显然是需要树分治，假如我们将所有种类的直径写出来 \(k_ix+b_i\)，那么我们将它们转化为半平面 \(y\geq k_ix+b_i\) 再求交即可。

考虑一种树分治，就是点分治，处理出每棵子树的路径信息，然后不断取出两棵大小最小的子树，统计跨过这两棵子树的路径信息，再将它们合并成一棵新的子树，再放回去（也就是合并果子）。可以证明这样访问到的点数为 \(O(n\log n)\)，具体怎么证见下文。

那么我们实际上要做的就只有：有两个半平面 \(y\geq k_ix+b_i\) 的集合 \(A, B\)，你需要求出集合 \(C=\{y\geq (k_1+k_2)x+(b_1+b_2)\ |\ (y\geq k_1x+b_1)\in A, (y\geq k_2x+b_2)\in B \}\)。这个太难了。考虑点 - 线对偶，将所有半平面 \(y\geq k_ix+b_i\) 对偶为点 \((k_i, -b_i)\)，然后只需要求 \(A\) 的对偶点集的凸包与 \(B\) 的对偶点集的凸包的闵可夫斯基和即可。这里还涉及一个上下凸包的问题，可以记一下结论，\(y\geq k_ix+b_i\) 的半平面交对偶之后是下凸包。

到这里题目就结束了，整理一下，求出需要合并的半平面集合 \(\{y\geq k_ix+b_i\}\) 后，将它们对偶为 \((k_i, -b_i)\)，然后分别求下凸包，求闵可夫斯基和，然后将求出来的点全部加到答案点集里面。得到答案点集后再求下凸包，最后转化回半平面交的形式，然后线性求出答案。复杂度 \(O(n\log^2n+m)\)。

点分治复杂度证明

考虑一种树分治，就是点分治，处理出每棵子树的路径信息，然后不断取出两棵大小最小的子树，统计跨过这两棵子树的路径信息，再将它们合并成一棵新的子树，再放回去（也就是合并果子）。可以证明这样访问到的点数为 \(O(n\log n)\)，具体怎么证见下文。

关于哈夫曼树的引理

首先先证明对于一个长度为 \(m\) 总和为 \(s\) 的序列，对它建哈夫曼树（也就是合并果子的操作树），则值 \(a\) 的深度是 \(O (\log\frac s a)\)。这是因为考虑合并果子的过程，大概如下图所示，我们接下来证明 \(a+b+c\geq 2a\) 就能说明 \(a\) 的深度为 \(O(\log \frac s a)\) 了。

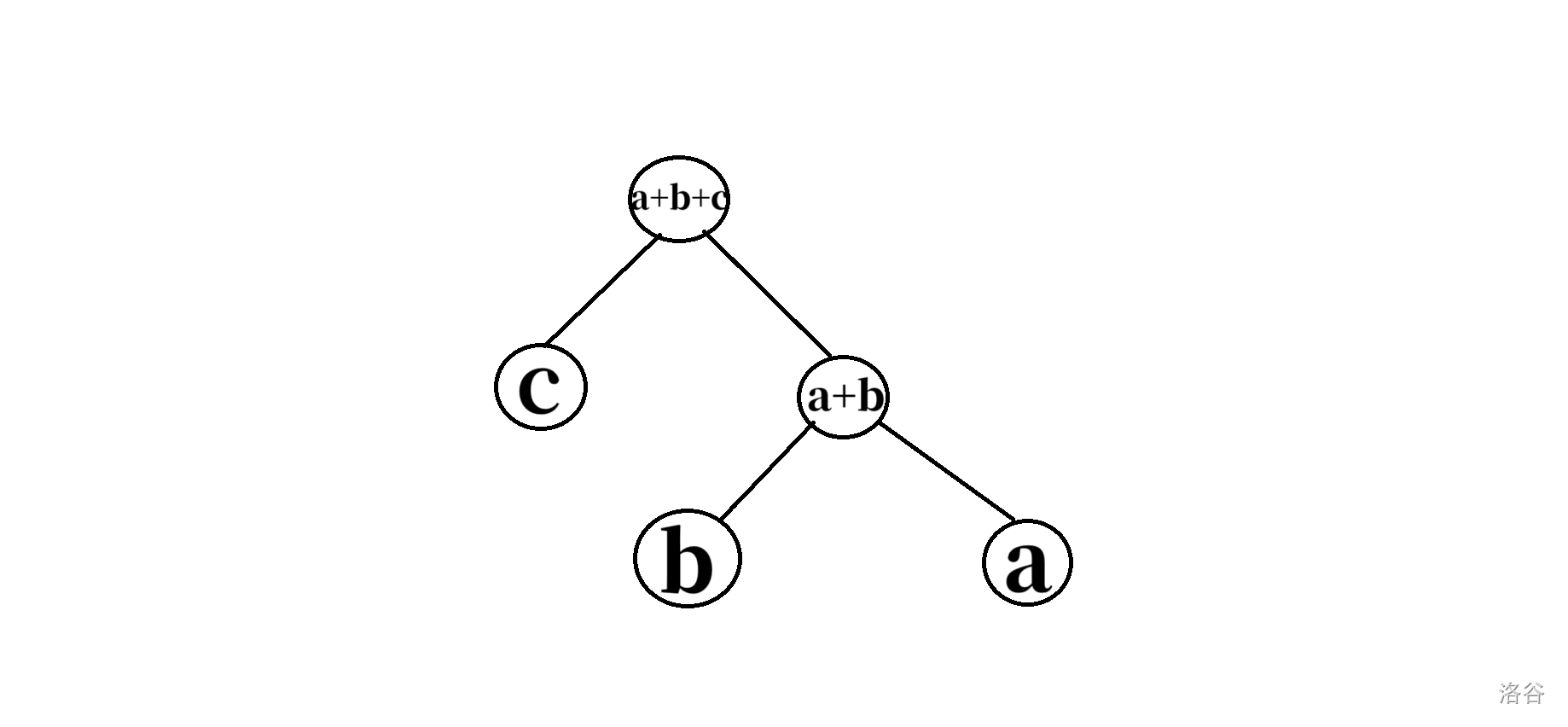
如果 \(b\geq a\)，那么结论就成立了。否则，如果 \(c\geq a\)，那么也成立了，现在就变成 \(b, c<a\) 的情况，可以发现这不可能，\(b, c\) 会先合并到一起，而不是 \(b, a\) 合并。

证明

令 \(T (u)\) 为点分树上 \(u\) 以及 \(u\) 子树算答案时会访问多少点。

\[T(u)=\sum_{v\in son(u)}siz_v\log\frac{siz_u}{siz_v}+\sum_{v\in son(u)} T(v) \]

也就是

\[T(u)=siz_u\log siz_u-\sum_{v\in son(u)}siz_v\log{siz_v}+\sum_{v\in son(u)} T(v) \]

发现 \(siz_u\log siz_u\) 重复出现，它会被它的点分树父亲算 \(-1\) 遍，自己算 \(+1\) 遍，那么 \(T(root)\) 自然就是 \(siz_{root}\log siz_{root}=O(n\log n)\)。

注意，\(O(\log \frac{siz_u}{siz_v})\) 这一项其实是有一点常数的，意思是所有子树都需要至少遍历一次，但是由点分树的性质，这部分也不超过 \(O (n\log n)\)。

代码

1. 特判 \(n=1\)。
2. 叉积要开 __int128。
3. 注意仔细处理三点共线和横坐标相同的情况，这会影响闵可夫斯基和正确性，特别是两个点的 \(x\) 坐标相同时，下凸包保留 \(y\) 最小的点，上凸包保留 \(y\) 最大的点。
4. 代码里把 \(y\geq k_ix+b_i\) 对偶成了 \((k_i, b_i)\) 因此求的是上凸包。

#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define endl "\n"
#define debug(...) void(0)
#endif
using LL = long long;
using int128_t = __int128;
constexpr int N = 1e5 + 10;
struct dot {
  LL x, y;
  dot operator+(const dot& rhs) const { return {x + rhs.x, y + rhs.y}; }
  dot operator-(const dot& rhs) const { return {x - rhs.x, y - rhs.y}; }
  friend int128_t det(const dot& lhs, const dot& rhs) { return (int128_t)lhs.x * rhs.y - (int128_t)lhs.y * rhs.x; }
  bool operator<(const dot& rhs) const { return x != rhs.x ? x < rhs.x : y < rhs.y; }
};
int n, m, siz[N], smx[N];
bool cut[N];
vector<tuple<int, int, int>> g[N];
int getroot(int u, int fa, int T) {
  int rt = 0;
  siz[u] = 1, smx[u] = 0;
  for (auto [v, k, b]: g[u]) if (!cut[v] && v != fa) {
    int nrt = getroot(v, u, T);
    if (smx[nrt] < smx[rt]) rt = nrt;
    siz[u] += siz[v], smx[u] = max(smx[u], siz[v]);
  }
  smx[u] = max(smx[u], T - siz[u]);
  return smx[u] < smx[rt] ? u : rt;
}
struct compare {
  bool operator()(const vector<dot>& lhs, const vector<dot>& rhs) {
    return lhs.size() > rhs.size();
  }
};
vector<dot> ans;
void dfs(int u, int fa, dot pre, vector<dot>& vec) {
  vec.push_back(pre);
  ans.push_back(pre);
  for (auto [v, k, b]: g[u]) if (!cut[v] && v != fa) {
    dfs(v, u, pre + dot{k, b}, vec);
  }
}
vector<dot> cvh(const vector<dot>& vec) {
  assert(is_sorted(vec.begin(), vec.end()));
  vector<dot> ret;
  for (dot p : vec) {
    if (!ret.empty() && ret.back().x == p.x) ret.pop_back();
    while (ret.size() >= 2 && det(p - ret.back(), ret.end()[-2] - ret.back()) >= 0) ret.pop_back();
    ret.push_back(p);
  }
  return ret;
}
vector<dot> minkowski(vector<dot> lhs, vector<dot> rhs) {
  if (lhs.empty() || rhs.empty()) return {};
  vector<dot> c{lhs[0] + rhs[0]};
  for (int i = (int)lhs.size() - 1; i >= 1; i--) lhs[i] = lhs[i] - lhs[i - 1];
  for (int i = (int)rhs.size() - 1; i >= 1; i--) rhs[i] = rhs[i] - rhs[i - 1];
  merge(lhs.begin() + 1, lhs.end(), rhs.begin() + 1, rhs.end(), back_inserter(c), [&](dot p, dot q) { return det(p, q) < 0; });
  for (int i = 1; i < (int)c.size(); i++) c[i] = c[i - 1] + c[i];
  return c;
}
void solve(int rt) {
  priority_queue<vector<dot>, vector<vector<dot>>, compare> pq;
  for (auto [v, k, b]: g[rt]) if (!cut[v]) {
    vector<dot> vec;
    dfs(v, rt, {k, b}, vec);
    sort(vec.begin(), vec.end());
    pq.push(vec);
  }
  while (pq.size() >= 2) {
    auto lhs = pq.top(); pq.pop();
    auto rhs = pq.top(); pq.pop();
    auto ret = minkowski(cvh(lhs), cvh(rhs));
    ans.insert(ans.end(), ret.begin(), ret.end());
    vector<dot> nxt(lhs.size() + rhs.size());
    merge(lhs.begin(), lhs.end(), rhs.begin(), rhs.end(), nxt.begin());
    pq.push(nxt);
  }
  cut[rt] = true;
  for (auto [v, k, b]: g[rt]) if (!cut[v]) solve(getroot(v, rt, siz[v]));
}
int main() {
#ifndef LOCAL
  cin.tie(nullptr)->sync_with_stdio(false);
#endif
  smx[0] = 1e9;
  cin >> n >> m;
  if (n == 1) {
    for (int i = 0; i < m; i++) cout << 0 << " \n"[i == m - 1];
    return 0;
  }
  for (int i = 1, u, v, k, b; i < n; i++) {
    cin >> u >> v >> k >> b;
    g[u].emplace_back(v, k, b);
    g[v].emplace_back(u, k, b);
  }
  solve(getroot(1, 0, n));
  sort(ans.begin(), ans.end());
  ans = cvh(ans);
  for (auto p : ans) debug("y >= %lldx%+lld\n", p.x, p.y);
  for (int i = 0, j = 0; i < m; i++) {
    while (j + 1 < (int)ans.size() && ans[j].x * i + ans[j].y < ans[j + 1].x * i + ans[j + 1].y) j++;
    cout << ans[j].x * i + ans[j].y << " \n"[i == m - 1];
  }
  return 0;
}