题解 P8426【[JOI Open 2022] 放学路（School Road）】

题解：P8426 [JOI Open 2022] 放学路（School Road）

题目描述

河狸国由 \(N\) 座城市组成，编号为 \(1 \sim N\)。共有 \(M\) 条道路连接这些城市，道路编号为 \(1 \sim M\)。道路 \(i\)（\(1 \le i \le M\)）双向连接城市 \(A_i\) 和 \(B_i\)，并且道路 \(i\) 的长度为 \(C_i\)。保证经过一定数量的道路，均可以从任意一座城市到达任意其他城市。

Bitaro 是一只住在城市 \(1\) 的河狸。他要去城市 \(N\) 上学。他上学通常都走一样的路线。他的上学路线满足如下条件。

• 令 \(L\) 为从城市 \(1\) 到城市 \(N\) 的最短距离。
• Bitaro 的上学路是一条连接城市 \(1\) 和城市 \(N\) 且长度为 \(L\) 的路径。

因为今天天气好，Bitaro 决定绕路回家。也就是说，他会选择一条从城市 \(N\) 到城市 \(1\) 且长度大于 \(L\) 的路径。因为 Bitaro 很容易厌倦，他不想经过同一座城市多于一次。因此，当他绕远路回家时，不允许经过同一座城市多于一次，并且不允许走回头路。

给定河狸国的城市和道路的信息，写一个程序确定是否存在一条从学校到 Bitaro 的家的远路。

赛时提醒：Bitaro 不允许在回家途中经过相同的城市超过一次，但是并不禁止经过在他上学路线中经过的城市。

对于所有数据，满足 \(2 \le N \le {10}^5\)，\(1 \le M \le 2 \times {10}^5\)，\(1 \le A_i < B_i \le N\)，\(1 \le C_i \le {10}^9\)，保证经过一定数量的道路，均可以从任意一个城市到达任意其他城市。

solution

虽然不知道为什么，但是首先发现这个图当起点是 \(1\) 终点是 \(4\) 的时候是一定无解的，因为 \(w(2, 3)\) 被迫为 \(0\)。

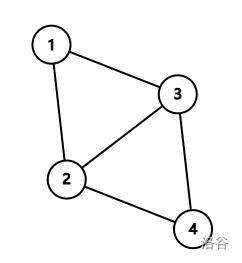
放宽一下，也就是说图中有 \(K_4\) 就无解。也不一定，如果 \(1\to n\) 任何路径都不经过这个结构也是有解的。假如能把 \(1\to n\) 到达不了的部分去掉，那么剩下就是广义串并联图了，直接广义串并联图方法启动。但是不能把 \(1, n\) 两个点删掉。结束以后可能还会有这种结构会被广义串并联图留着，因为 \(1, n\) 不能删，那么现在一定是 \(1, n\) 两个点有至少一个点的度数 \(\leq 2\) 阻拦了。轻轻地删一下度数 \(\leq 1\) 的点，然后就会分成两条链。这两条链之间如果有边连接，立即不合法；两条链之间可以分裂，可是一旦分裂出来的两条链之间有边连接就也不合法（除非是接回去到分裂点所在的链中），你再仔细思考一下，是不是说缩完二度点，这些链变成边之后，实际上会成为一个巨大的环，把 \(1\to n\) 这条边连上后环上的所有弦是不相交的。而这种形状会被广义串并联图方法缩成仅剩一条边，这就矛盾了，一开始根本不会分成两条链。也就是说不存在上图那种结构的时候，广义串并联图方法会将图缩成仅剩一条边。

我们整理一下，也就是说我们把 \(1\to n\) 到达不了的部分去掉，连上 \(1\to n\) 这条边，然后跑广义串并联图方法，由于上面那种结构会被升级为 \(K_4\)，因此如果跑完以后剩下的不只 \(1\to n\) 单独一条边，那么就肯定是因为出现了上面那种结构。

最后再考虑一下 \(1\to n\) 到达不了的部分怎么去掉，其实会比较自然，连上 \(1\to n\) 这条边，然后和 \(1, n\) 不在一个点双中的点直接忽略掉就肯定是对的了。然后跑广义串并联图方法，当且仅当剩下的只有 \(1\to n\) 单独一条边而且叠合重边时没有出现冲突时，答案为 \(0\)。

以上证明不是很严谨甚至不是很对，看一下就好了，真的要证明还得看官方题解。总之就是以复杂度 \(O(m\log m)\) 解决了本题。

code

#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define endl "\n"
#define debug(...) void(0)
#endif
using LL = long long;
constexpr int N = 1e5 + 10;
int n, m;
LL dis[N];
vector<pair<int, LL>> g[N];
void dijkstra(int s) {/*{{{*/
  static bool vis[N];
  using pii = pair<LL, int>;
  priority_queue<pii, vector<pii>, greater<pii>> q;
  memset(dis, 0x3f, sizeof dis);
  memset(vis, false, sizeof vis);
  q.emplace(dis[s] = 0, s);
  while (!q.empty()) {
    int u = q.top().second; q.pop();
    if (exchange(vis[u], true)) continue;
    for (auto [v, w] : g[u]) if (dis[v] > dis[u] + w) q.emplace(dis[v] = dis[u] + w, v);
  }
}/*}}}*/
vector<int> dcc;
int dfn[N], low[N], stk[N], top, cnt;
void tarjan(int u) {
  dfn[u] = low[u] = ++cnt, stk[++top] = u;
  for (auto [v, w] : g[u]) {
    if (dfn[v]) low[u] = min(low[u], dfn[v]);
    else {
      tarjan(v), low[u] = min(low[u], low[v]);
      if (low[v] >= dfn[u]) {
        vector<int> vec{u};
        do vec.push_back(stk[top]); while (stk[top--] != v);
        sort(vec.begin(), vec.end());
        if (vec[0] == 1 && vec.back() == n) dcc = vec;
      } 
    }
  }
}
map<int, LL> mp[N];
int main() {
#ifndef LOCAL
  cin.tie(nullptr)->sync_with_stdio(false);
#endif
  cin >> n >> m;
  for (int i = 1, u, v, w; i <= m; i++) {
    cin >> u >> v >> w;
    g[u].emplace_back(v, w);
    g[v].emplace_back(u, w);
  }
  dijkstra(1);
  g[1].emplace_back(n, dis[n]);
  g[n].emplace_back(1, dis[n]);
  for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i);
  assert(!dcc.empty());
  for (int u : dcc) {
    for (auto [v, w] : g[u]) if (binary_search(dcc.begin(), dcc.end(), v)) {
      if (mp[u].count(v) && mp[u][v] != w) mp[u][v] = -1; else mp[u][v] = w;
    }
  }
  for (int u : dcc) for (auto [v, w] : mp[u]) if (u < v) debug("-> %d %d %lld\n", u, v, w);
  static int deg[N];
  queue<int> q;
  for (int i : dcc) if ((deg[i] = (int)mp[i].size()) <= 2) q.push(i);
  while (!q.empty()) {
    int u = q.front(); q.pop();
    if (deg[u] == 0 || u == 1 || u == n) continue;
    debug("u = %d\n", u);
    if (deg[u] == 1) {
      auto [x, w] = *mp[u].begin();
      mp[u].clear(), deg[u] = 0, mp[x].erase(u), deg[x] -= 1;
      if (deg[x] <= 2) q.push(x);
      assert(false);
    } else {
      auto [x, w1] = *mp[u].begin();
      auto [y, w2] = *mp[u].rbegin();
      mp[u].clear(), deg[u] = 0, mp[x].erase(u), mp[y].erase(u), deg[x] -= 1, deg[y] -= 1;
      auto w = w1 == -1 || w2 == -1 ? -1ll : w1 + w2;
      if (mp[x].count(y) && mp[x][y] != w) mp[x][y] = mp[y][x] = -1; else mp[x][y] = mp[y][x] = w;
      deg[x] = (int)mp[x].size(), deg[y] = (int)mp[y].size();
      if (deg[x] <= 2) q.push(x);
      if (deg[y] <= 2) q.push(y);
    }
  }
  for (int u : dcc) for (auto [v, w] : mp[u]) if (u < v) debug("-> %d %d %lld\n", u, v, w);
  for (int u : dcc) assert(deg[u] == (int)mp[u].size());
  bool flag = mp[1].size() == 1 && mp[n].size() == 1 && mp[1].count(n) && mp[1][n] != -1;
  for (int i : dcc) if (i != 1 && i != n && !mp[i].empty()) flag = false;
  cout << 1 - flag << endl;
  return 0;
}