【笔记】图论连通性 2

【笔记】图论连通性 2

不知道取什么标题。

Tarjan 科技、双连通理论

边双连通分量

在一张无向图上，如果有一条边，满足删去这条边后，图不连通，那么这条边被称为无向图的割边。

没有割边的图是边双连通的，极大的边双连通子图为边双连通分量。

点双连通分量

在一张无向图上，如果有一个点，满足删去这个点后，图不连通，那么这个点被称为无向图的割点。

没有割点的图是点双连通的，极大的点双连通子图为点双连通分量。

点击查看代码

int n, m, dfn[N], low[N], stk[N], cnt, tot, top;
basic_string<int> g[N], tr[N << 1];
void tarjan(int u) {/*{{{*/
  dfn[u] = low[u] = ++cnt, stk[++top] = u;
  for (int v : g[u]) {
    if (dfn[v]) low[u] = min(low[u], dfn[v]);
    else {
      tarjan(v), low[u] = min(low[u], low[v]);
      if (low[v] >= dfn[u]) {
        int p = ++tot; // 初始时赋值 tot = n
        tr[p] += u, tr[u] += p;
        do tr[p] += stk[top], tr[stk[top]] += p; while (stk[top--] != v);
      }
    }
  }
}/*}}}*/

有一种能线性找到点双中所有边的写法。维护一个边的栈，在向下搜索时将边入栈，如果是搜索树上的返祖边也将边入栈。以下写法会在大小为 \(2\) 的点双上产生重边，可以考虑加一个编号以去重。

点击查看代码

int n, m, cid, tot, cnt, top, etop, dfn[N], low[N], stk[N;
vector<tuple<int, int, int>> E[N << 1], Estk;
vector<pair<int, int>> g[N];
basic_string<int> tr[N << 1];
void tarjan(int u) {
  dfn[u] = low[u] = ++cnt, stk[++top] = u;
  for (auto e : g[u]) {
    int v = e.first, w = e.second;
    auto edg = make_tuple(u, v, w);
    if (dfn[v]) {
      low[u] = min(low[u], dfn[v]);
      if (dfn[v] < dfn[u]) Estk.push_back(edg);
    } else {
      Estk.push_back(edg);
      tarjan(v), low[u] = min(low[u], low[v]);
      if (low[v] >= dfn[u]) {
        int p = ++tot;
        tr[p] += u, tr[u] += p;
        do tr[p] += stk[top], tr[stk[top]] += p; while (stk[top--] != v);
        E[p] = {edg};
        while (Estk.back() != edg) E[p].push_back(Estk.back()), Estk.pop_back();
        Estk.pop_back();
      }
    }
  }
}

点双连通性四条性质

来自 P8456 「SWTR-8」地地铁铁 - 洛谷专栏

性质 1：在一个点数 \(\geq 3\) 的点双中，给出任意两个不同的点，一定能找到经过它们的简单环。

简略证明：\(x, y\) 不相邻时可以使用 Menger 定理；否则考虑删去 \((x, y)\)，如果这时 \(x, y\) 不连通，则会产生一个割点。

性质 2：在一个点数 \(\geq 3\) 的点双中，给出一个点 \(x\) 和一条边，一定能找到经过它们的简单环。

点双两点应用性质 1 得证。

性质 3：在一个点数 \(\geq 3\) 的点双中，给出两个不同的点 \(x, y\) 和一条边 \(e\)，一定能找到 \(x\to e\to y\) 的简单路径。

简略证明：先对 \(x, e\) 应用性质 2，如果这条路径无法延伸至 \(y\)，则会有一个割点产生。

性质 4：在一个点数 \(\geq 3\) 的点双中，给出三个不同的点 \(x, y,z\)，一定能找到 \(x\to z\to y\) 的简单路径。

简略证明：找到与 \(z\) 相连的一条边 \(e\)，对 \(x, y, e\) 应用性质 3 得证。

由于点双的良好结构，在其上的很多种路径都能找到，这都归功于“点双连通分量没有割点”这一性质。

一些复习题

P4630 [APIO2018] 铁人两项

由于要求简单路径不能经过重复点，考虑建圆方树。枚举 \(c\)，然后可以计算答案，然后尝试换根就行。这题换根很简单。

P8456 「SWTR-8」地地铁铁

由于要求简单路径不能经过重复点，考虑建圆方树。使用上面列举的点双连通性四条性质，其它部分不难。

P7353 [2020-2021 集训队作业] Tom & Jerry

由于要求……嗯？由于要求 Jerry 的路径不能与 Tom 的位置重叠，这里就蕴含了一种割点的想法，考虑建圆方树。

如果一个圆点不能一步杀穿它相邻某个方点的点双中所有点，那么将这条边定向为圆点到方点。由于一个点双内不能有恰好一个圆点不能一步杀，我们仔细分讨一下，就会发现：

1. 如果有两个方点 \(x, y\)，它们之间的路径形如 \(x- u- \cdots- v- y\)，如果发现 \(u\to x\) 和 \(v\to y\) 这两条边被定向了，那么标记 \((x, y)\) 为好的点对。询问 \(a, b\) 时，删去 \(a\)，若有一个好的点对的其中一端在 \(b\) 所在连通块中，那么 Jerry 就获胜了（Jerry 可以在这两个方点中来回横跳）。
2. 还有一种情况，如果一个方点上没有点定向到它，而同时 Jerry 一开始可以到达这个方点，那么 Jerry 也获胜了。

看一下官方题解写的东西，证明一下两者是等价的。

• 定义点对 \((x, y)\) 是好的，当且仅当圆方树上路径 \(x \to y\) 上任意两个相邻的圆点在原图 G 上也相邻。
• Tom 能获胜，当且仅当以下两个条件成立至少一个：
  • 存在一个点 \(u\)，使得对于任意的 \(x\)，\((u, x)\) 是好的；
  • 对于删去 \(a\) 后 \(b\) 所在的连通块中任意一点 \(x\)，\((a, x)\) 是好的。

1. 如果我的结论能推断出 Jerry 获胜，那么 ix35 的结论就不能推出 Tom 获胜。
2. 如果 ix35 的结论能推断出 Tom 获胜，那么我就找不到我的好的点对，我的结论不能推断出 Jerry 获胜。
3. 由于我的结论和 ix35 的结论不能同时推断不出 Jerry / Tom 获胜，因此我的结论和 ix35 的结论是等价的。

至此可以平方完成，然后就用其它技术例如树上倍增之类的优化一下就可以了。

QOJ3301 Economic One-way Roads

这题是耳分解 的 \(O(2^nn^3)\) DP 题，以后复习的时候可以看一下。

P9394 白鹭兰

这题是“点双连通 耳分解 双极定向”题，看 ix35 题解算了 白鹭兰 - 洛谷专栏。

平面图相关理论

平面图相关理论和点双连通分量的联系紧密，所以放在一起了。

平面图

无向图 \(G\) 是平面图当且仅当 \(G\) 不含与 \(K_5\) 或 \(K_{3,3}\) 同胚的子图。

对于有 \(n\) 个点 \(m\) 条边 \(r\) 个面 \(p\) 个连通块的平面图，满足欧拉公式 \(n-m+r=p+1\)。注意面数 \(r\) 包含一个面积无限的外部面。

若 \(G\) 为 \(n\geq 3\) 个点 \(m\) 条边的平面图，则 \(m\leq 3n-6\)。

广义串并联图

无向图 \(G\) 是广义串并联图当且仅当 \(G\) 不含与 \(K_4\) 同胚的子图。

广义串并联图可以通过广义串并联图方法缩成一个点：删一度点、缩二度点、叠合重边。

外平面图

无向图 \(G\) 是外平面图当且仅当它是平面图且所有顶点都可以在某一个面的边界上。

无向图 \(G\) 是外平面图当且仅当 \(G\) 不含与 \(K_4\) 或 \(K_{2,3}\) 同胚的子图。

外平面图的一个点双连通分量的形状就像一个有若干条不相交对角线的多边形，或者说是一个环以及环中的一些不相交的弦。你可以发现有时候说的“三角剖分”图就是外平面图。

以上三种图的联系

已知：\(K_5\) 含有与 \(K_4, K_{2, 3}\) 同胚的子图，\(K_{3, 3}\) 含有与 \(K_4, K_{2, 3}\) 同胚的子图。

图	\(K_4\)	\(K_{2,3}\)	\(K_5\)	\(K_{3,3}\)
平面图	有	有	无	无
广义串并联图	无	有	无	无
外平面图	无	无	无	无

由此可以发现以上三种图有一种隐晦的包含关系。

\(K_{3,2}\) 也就是 \(K_{\geq 3, 2}\) 这样的图有时被称作杏仁，杏仁一定是点双连通的，图中一旦含有杏仁就会丢失外平面图相关的性质。

广义串并联图操作

通过不断地进行删一度点、缩二度点、叠合重边的操作，\(n\) 个点 \(n+k\) 条边的无向图 \(G\) 最终会变成点数不超过 \(2k\)、边数不超过 \(3k\) 的无向图。

一些复习题 2

P8426 [JOI Open 2022] 放学路（School Road）

虽然不知道为什么，但是首先发现这个图当起点是 \(1\) 终点是 \(4\) 的时候是一定无解的，因为 \(w(2, 3)\) 被迫为 \(0\)。

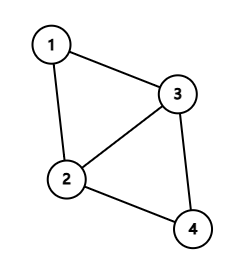
放宽一下，也就是说图中有 \(K_4\) 就无解。也不一定，如果 \(1\to n\) 任何路径都不经过这个结构也是有解的。假如能把 \(1\to n\) 到达不了的部分去掉，那么剩下就是广义串并联图了，直接广义串并联图方法启动。但是不能把 \(1, n\) 两个点删掉。结束以后可能还会有这种结构会被广义串并联图留着，因为 \(1, n\) 不能删，那么现在一定是 \(1, n\) 两个点有至少一个点的度数 \(\leq 2\) 阻拦了。轻轻地删一下度数 \(\leq 1\) 的点，然后就会分成两条链。这两条链之间如果有边连接，立即不合法；两条链之间可以分裂，可是一旦分裂出来的两条链之间有边连接就也不合法（除非是接回去到分裂点所在的链中），你再仔细思考一下，是不是说缩完二度点，这些链变成边之后，实际上会成为一个巨大的环，把 \(1\to n\) 这条边连上后环上的所有弦是不相交的。而这种形状会被广义串并联图方法缩成仅剩一条边，这就矛盾了，一开始根本不会分成两条链。也就是说不存在上图那种结构的时候，广义串并联图方法会将图缩成仅剩一条边。

我们整理一下，也就是说我们把 \(1\to n\) 到达不了的部分去掉，连上 \(1\to n\) 这条边，然后跑广义串并联图方法，由于上面那种结构会被升级为 \(K_4\)，因此如果跑完以后剩下的不只 \(1\to n\) 单独一条边，那么就肯定是因为出现了上面那种结构。

最后再考虑一下 \(1\to n\) 到达不了的部分怎么去掉，其实会比较自然，连上 \(1\to n\) 这条边，然后和 \(1, n\) 不在一个点双中的点直接忽略掉就肯定是对的了。然后跑广义串并联图方法，当且仅当剩下的只有 \(1\to n\) 单独一条边而且叠合重边时没有出现冲突时，答案为 \(0\)。

以上证明不是很严谨甚至不是很对，看一下就好了，真的要证明还得看官方题解。总之就是以复杂度 \(O(m\log m)\) 解决了本题。

P11832 [省选联考 2025] 图排列

可以感受到本题的图就是外平面图，或者看外平面图的定义也能感受到。建点双的圆方树，找出每个点双的环（用广义串并联图方法），然后再去决定方案。