题解:P12196 [NOISG2025 Prelim] Lasers 2
题解:P12196 [NOISG2025 Prelim] Lasers 2
题目描述
Pavement 从 Gohcart 那里购买了一个激光玩具(Gohcart 原先是从 Rar the Cat 那里买的)。这个玩具有一个由 \(h\) 行 \(w\) 列组成的网格。网格的行编号从上到下为 \(1\) 到 \(h\),列编号从左到右为 \(1\) 到 \(w\)。
每一行恰好包含一个上锁的滑动墙。初始时,第 \(i\) 行的墙覆盖第 \(l[i]\) 列到第 \(r[i]\) 列(从 \(1\) 开始编号),解锁它需要花费 \(c[i]\) 美元。墙一旦解锁,就可以在第 \(i\) 行上水平滑动到任意位置,只要它对齐在网格的边缘内即可。墙的任何部分都不能超出玩具的左边缘或右边缘。
每一列的顶部都有一个朝下的激光。如果某个滑动墙位于第 \(i\) 列,那么它将阻挡第 \(i\) 列上的激光。
一个可能的玩具示例如下,其中 \(h = 3\),\(w = 10\):
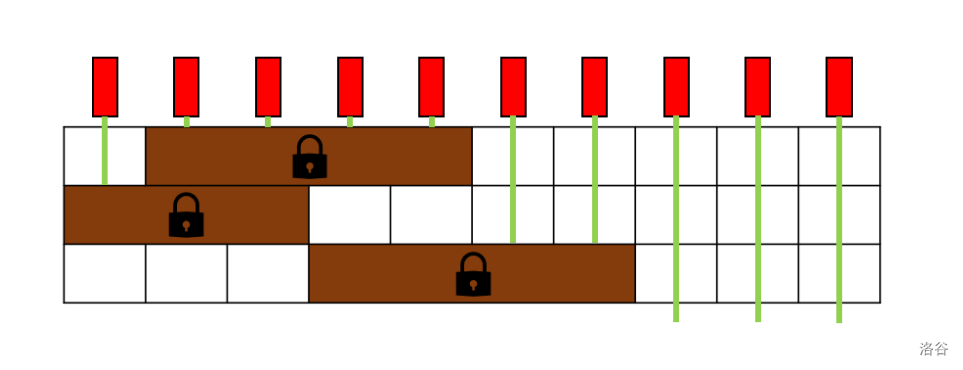
给定总预算 \(k\) 美元,Pavement 的目标是在合理解锁并滑动墙壁的情况下,最大化未被阻挡的激光数量。请你确定他最多可以实现多少束未被阻挡的激光。
- \(1 \leq h, w \leq 2000\)
- \(0 \leq k \leq 10^9\)
- 对所有 \(1 \leq i \leq h\),满足 \(1 \leq l[i] \leq r[i] \leq w\)
- 对所有 \(1 \leq i \leq h\),满足 \(0 \leq c[i] \leq 10^9\)
solution
因为我们可以将所有激活墙全部放在最长的激活墙后面,而如果最长的激活墙比最长未激活墙短(也就是全场最长墙未激活),那么答案就是未激活墙的并的大小,否则我们需要找一个地方放置这个激活的全场最长墙,然后答案是未激活墙的并再并上这个最长墙的大小。
一堆区间的并还是太困难了,我们不妨按照并的连续段进行 dp。我们把问题改成最大化选中的区间的价格的和(也就是我们着眼于的是未激活的墙),先处理一个 \(sum[l,r]\) 表示所有 \(\subseteq[l, r]\) 的区间的价格,然后直接 dp,设 \(f_i\) 表示考虑完 \([1, i]\) 的选择情况的最大价格,转移就 \(O(n)\) 转移 \(f_i=\max_{j\leq i}f_{j-1}+sum_{j, i}\)。这只是一个雏形,我们还需要的是:
- 需要有一个连续段的长度大于全场最长墙,然后再看看能不能计入全场最长墙的价格。使用一个
0/1记录即可。 - 需要记答案,记录有多少个空位(记作变量 \(w\))。使用 \(O(n)\) 的时空代价即可。
此时复杂度 \(O(n^3)\),需要优化。
发现我们将前面的 \(O(n^2)\) 个状态排成矩阵的形式,那么就是形如矩阵的某一列对位加上 \(sum\) 的某一列的最大值贡献到 \(f_{i, w}\),且随着 \(i\) 增加这些列不会变,只有 \(sum\) 的那一列会增加。然而这样的话可以不在一开始处理 \(sum\),而是 \(i\) 增加的时候将右端点为 \(i\) 的区间拿出来将每列的某个前缀进行整体加。所以我们对每一列用线段树维护即可,需要支持区间加和区间最大值(因为有一个“连续段的长度大于全场最长墙”的特殊转移需要区间最大值)。由于区间个数是 \(O(n)\) 的,复杂度做到 \(O(n^2\log n)\) 也就是 \(O(hw\log w)\)。
code
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define debug(...) void(0)
#define endl "\n"
#endif
using LL = long long;
template <class T> T& chkmin(T& x, const T& y) { return x = min(x, y); }
template <class T> T& chkmax(T& x, const T& y) { return x = max(x, y); }
constexpr int N = 2010;
struct wall {
int l, r, c;
int length() const { return r - l + 1; }
friend bool operator<(const wall& lhs, const wall& rhs) { return lhs.length() < rhs.length(); }
};
struct segtree {
LL ans[N << 2], tag[N << 2];
segtree() {
memset(ans, ~0x3f, sizeof ans);
memset(tag, 0, sizeof tag);
}
void spread(int p, LL k) { tag[p] += k, ans[p] += k; }
void maintain(int p) { ans[p] = max(ans[p << 1], ans[p << 1 | 1]); }
void pushdown(int p) { spread(p << 1, tag[p]), spread(p << 1 | 1, tag[p]), tag[p] = 0; }
void setValue(int x, LL v, int p, int l, int r) {
if (l == r) return ans[p] = v, void();
int mid = (l + r) >> 1;
pushdown(p);
if (x <= mid) setValue(x, v, p << 1, l, mid);
else setValue(x, v, p << 1 | 1, mid + 1, r);
maintain(p);
}
void modify(int ql, int qr, LL k, int p, int l, int r) {
if (ql <= l && r <= qr) return spread(p, k);
int mid = (l + r) >> 1;
pushdown(p);
if (ql <= mid) modify(ql, qr, k, p << 1, l, mid);
if (mid < qr) modify(ql, qr, k, p << 1 | 1, mid + 1, r);
maintain(p);
}
LL query(int ql, int qr, int p, int l, int r) {
if (ql <= l && r <= qr) return ans[p];
int mid = (l + r) >> 1;
pushdown(p);
LL ret = -1e18;
if (ql <= mid) chkmax(ret, query(ql, qr, p << 1, l, mid));
if (mid < qr) chkmax(ret, query(ql, qr, p << 1 | 1, mid + 1, r));
return ret;
}
} tr[N][2];
int n, m;
LL lim, f[N][2][N];
vector<wall> rgs[N];
int main() {
#ifndef NF
cin.tie(nullptr)->sync_with_stdio(false);
#endif
cin >> m >> n >> lim, lim = -lim;
wall maxw = {0, -1, 0};
for (int i = 1, l, r, c; i <= m; i++) cin >> l >> r >> c, lim += c, rgs[r].push_back({l, r, c}), maxw = max(maxw, wall{l, r, c});
rgs[maxw.r].push_back({maxw.l, maxw.r, -maxw.c});
memset(f, ~0x3f, sizeof f);
f[0][0][0] = 0;
for (int i = 1; i <= n; i++) {
f[i][0][0] = 0;
for (int t : {0, 1}) {
for (int w = 1; w <= i; w++) {
auto& seg = tr[w - i + n][t];
seg.setValue(i, f[i - 1][t][w - 1], 1, 1, n);
for (auto wl : rgs[i]) seg.modify(1, wl.l, wl.c, 1, 1, n);
chkmax(f[i][t][w], max(seg.ans[1], f[i - 1][t][w]));
if (t == 0 && i >= maxw.length()) {
if (maxw.r <= i) seg.modify(1, maxw.l, maxw.c, 1, 1, n);
chkmax(f[i][1][w], seg.query(1, i - maxw.length() + 1, 1, 1, n));
if (maxw.r <= i) seg.modify(1, maxw.l, -maxw.c, 1, 1, n);
}
}
}
}
for (int i = 1; i <= n; i++) {
for (int t : {0, 1}) {
for (int w = 0; w <= n; w++) if (f[i][t][w] >= 0) debug("f[%d][%d][%d] = %lld\n", i, t, w, f[i][t][w]);
}
}
for (int w = 0; w <= n; w++) if (f[n][1][w] >= lim) return cout << n - w << endl, 0;
assert(false);
return 0;
}
以下是暴力代码,可以参考一下。
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define debug(...) void(0)
#define endl "\n"
#endif
using LL = long long;
template <class T> T& chkmin(T& x, const T& y) { return x = min(x, y); }
template <class T> T& chkmax(T& x, const T& y) { return x = max(x, y); }
constexpr int N = 2010;
struct wall {
int l, r, c;
int length() const { return r - l + 1; }
friend bool operator<(const wall& lhs, const wall& rhs) { return lhs.length() < rhs.length(); }
};
int n, m;
LL lim, sum[N][N];
vector<pair<int, LL>> f[N][2];
int main() {
#ifndef NF
cin.tie(nullptr)->sync_with_stdio(false);
#endif
cin >> m >> n >> lim, lim = -lim;
wall maxw = {0, -1, 0};
for (int i = 1, l, r, c; i <= m; i++) cin >> l >> r >> c, lim += c, sum[l][r] += c, maxw = max(maxw, wall{l, r, c});
sum[maxw.l][maxw.r] -= maxw.c;
for (int l = n; l >= 1; l--) {
for (int r = 1; r <= n; r++) sum[l][r] += sum[l + 1][r];
}
for (int l = 1; l <= n; l++) {
for (int r = 1; r <= n; r++) sum[l][r] += sum[l][r - 1];
}
f[0][0].emplace_back(0, 0);
for (int i = 1; i <= n; i++) {
static LL tmp[2][N];
for (int t : {0, 1}) {
fill(tmp[t], tmp[t] + i + 1, -1e18);
for (auto [w, sv] : f[i - 1][t]) chkmax(tmp[t][w], sv);
for (int j = i; j >= 1; j--) {
for (auto [w, sv] : f[j - 1][t]) chkmax(tmp[t][w + i - j + 1], sv + sum[j][i]);
}
}
for (int j = i - maxw.length() + 1; j >= 1; j--) {
for (auto [w, sv] : f[j - 1][0]) chkmax(tmp[1][w + i - j + 1], sv + sum[j][i] + (j <= maxw.l && maxw.r <= i ? maxw.c : 0));
}
for (int t : {0, 1}) {
for (int w = 0; w <= i; w++) if (tmp[t][w] >= 0) debug("f[%d][%d][%d] = %lld\n", i, t, w, tmp[t][w]);
LL pre = -1;
for (int j = 0; j <= i; j++) if (pre < tmp[t][j]) f[i][t].emplace_back(j, pre = tmp[t][j]);
}
}
for (auto [w, sv] : f[n][1]) if (sv >= lim) return cout << n - w << endl, 0;
assert(false);
return 0;
}
本文来自博客园,作者:caijianhong,转载请注明原文链接:https://www.cnblogs.com/caijianhong/p/18737441/solution-P12196



 浙公网安备 33010602011771号
浙公网安备 33010602011771号