题解 P9885 / QOJ6126【[Qingdao18A] Sequence and Sequence】

题解：P9885 / QOJ6126 [Qingdao18A] Sequence and Sequence

具体数学还在发力！

题目描述

考虑下列两个序列 \(P\) 和 \(Q\)。我们用 \(P(i)\) 表示序列 \(P\) 中的第 \(i\) 个元素，用 \(Q(i)\) 表示序列 \(Q\) 中的第 \(i\) 个元素：

序列 \(P\) 是一个已排序的序列，其中，对于所有 \(k \in \mathbb{Z^+}\)，\(k\) 在序列 \(P\) 中出现 \((k+1)\) 次（\(\mathbb{Z^+}\) 为正整数集）。也就是说，\(P = \{1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 6, \dots \}\)
序列 \(Q\) 可以由以下方程导出：

\[\begin{cases} Q(1) = 1 & \\ Q(i) = Q(i-1) + Q(P(i)) & \text{if } i > 1 \end{cases} \]

也就是说，\(Q = \{1, 2, 4, 6, 8, 12, 16, 20, 24, 30, 36, 42, 48, 54, 62, \dots \}\)。

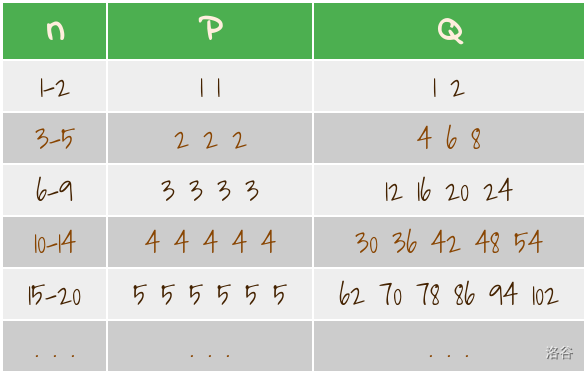
给定一个正整数 \(n\)，请计算 \(Q(n)\) 的值。

输入格式

本题的测试点包含多组测试数据。

第一行输入包含一个整数 \(T\) （\(10^4\) 左右），表示测试数据的数量。对于每组测试数据：

第一行（也是唯一一行）包含一个整数 \(n\) （\(1 \le n \le 10^{40}\)）。

输出格式

对于每组测试数据，输出一行，包含一个整数，表示 \(Q(n)\) 的值。

1. Abel 分部求和公式

数分笔记——Abel 分部求和公式 - 知乎

\(A_i=\sum_{j=1}^ia_j\)。

\[\sum_{i=1}^na_ib_i=A_nb_n-\sum_{i=1}^{n-1}A_i(b_{i+1}-b_i) \]

因为左式

\[\begin{aligned} =&\sum_{i=1}^n(A_i-A_{i-1})b_i\\ =&\sum_{i=1}^nA_ib_i-\sum_{i=1}^nA_{i-1}b_i\\ =&\sum_{i=1}^nA_ib_i-\sum_{i=0}^{n-1}A_{i}b_{i+1}\\ =&A_nb_n-A_0b_1+\sum_{i=1}^{n-1}A_i(b_i-b_{i+1})\\ \end{aligned} \]

等于右式。这里我们默认 \(A_0=0\) 了。下标从 \(1\) 开始就是神经。

2. 从有限微积分出发的分部求和

有限微积分与数列求和 - 洛谷专栏

准备应用

\[\sum u\Delta v=uv-\sum \textrm E v\Delta u \]

记 \(F(x)=\sum f(x)\delta x\)，这样就有 \(u(x)=Q(P(x)),v(x)=F(x)\)，可以发射导弹。

\[Q(n)=\sum_{1}^{n+1} Q(P(x))f(x)\delta x=F(x)Q(P(x))\mid_1^{n+1}-\sum_1^{n+1} F(x+1)(Q(P(x+1))-Q(P(x)))\delta x \]

发现十分神经病。我们重定义一下，\(\Delta f(x)=f(x)-f(x-1)\)，这样左闭右开区间就变成左开右闭区间。然后乘法法则也需要审视一下。

\[\begin{aligned} \Delta f(x)g(x)=&f(x)g(x)-f(x-1)g(x-1)+f(x-1)g(x)-f(x-1)g(x)\\ =&\Delta f(x)g(x)+f(x-1)\Delta g(x) \end{aligned} \]

给我个符号，就用 \(\textrm L\)，表示 \(\textrm L f(x)=f(x-1)\)，那么

\[\Delta (uv)=v\Delta u+\textrm Lu\Delta v \]

这样也可以重新定义 \(\sum_a^b f(x)\delta x=\sum_{i=a+1}^bf(i)\)。

分部求和可以重新写一遍：

\[\sum v\Delta u=uv-\sum\textrm Lu\Delta v \]

刚才说的东西

\[\sum_{i=1}^na_ib_i=A_nb_n-\sum_{i=1}^{n-1}A_i(b_{i+1}-b_i)=A_nb_n-\sum_{i=1}^{n}A_{i-1}(b_i-b_{i-1}) \]

现在就能对起来了！

3. 题解

\[Q(n)=\sum_{i=1}^nQ(P(i)) \]

诱人的是 \(P(i)\) 取值的连续，我们想要将其用 \(Q(P(i))-Q(P(i-1))\) 的线性组合表示 \(Q(n)\)。

令 \(f(x)=1\)，则

\[Q(n)=\sum_{i=1}^nf(i)Q(P(i)) \]

令 \(F(n)=\sum_{i=1}^nf(i)\)。应用分部求和法，无论是上面的哪一种形式，总之我们有

\[Q(n)=\sum_{i=1}^nf(i)Q(P(i))=F(n)Q(P(n))-\sum_{i=1}^{n-1}F(i)(Q(P(i+1))-Q(P(i))) \]

取出右边和式：注意 \(F(0)\) 被我们默认为 \(0\)。

\[\begin{aligned} &\sum_{i=1}^{n-1}F(i)(Q(P(i+1))-Q(P(i)))\\ =&\sum_{i=1}^{n}F(i-1)(Q(P(i))-Q(P(i-1)))\\ =&\sum_{i=1}^{P(n)}F(i(i+1)/2-1)(Q(i)-Q(i-1))\\ =&\sum_{i=1}^{P(n)}F(i(i+1)/2-1)Q(P(i))\\ \end{aligned} \]

最后一步由定义得到。所以记 \(g(f, n)=\sum_{i=1}^nf(i)Q(P(i))\) 则

\[g(f, n)=F(n)Q(P(n))-g(h, P(n))=F(n)g(I, P(n))-g(h, P(n)) \]

其中 \(F(n)=\sum_{i=1}^nf(i)\)、\(h(i)=F(i(i+1)/2-1)\)，总是可以算的。\(Q(n)=g(I, n)\)。

因为 \(P(n)=O(\sqrt n)\)，大概迭代三次 \(P(P(P(n)))\leq 10^6\) 就直接计算了。注意 \(g\) 一开始的定义，暴力不要求错东西。

4. 代码实现

实现比较困难，第一是高精度，这个直接使用板子（强烈推荐封装 BigInt 的伟大计划 - 洛谷专栏、剪贴板直达）就算了，真考了就写 python。

第二是 \(F(n)=\sum_{i=1}^nf(i)\)、\(h(i)=F(i(i+1)/2-1)\) 这个鬼畜的东西，又有前缀和又有二次函数复合。正常做法是拉格朗日插值。但是我们有高精度，控制不好的话会有麻烦。

考虑使用 python3 的 sympy 库（正赛没有这个库可以用），具体用法你自己问 AI，反正能写出来个这东西：

#!/bin/env python3
import sympy

x = sympy.Symbol('x')
i = sympy.Symbol('i')

def presum(f):
    return sympy.Sum(f.subs(x, i), (i, 1, x)).doit().simplify()

def uplevel(F):
    return F.subs(x, x * (x + 1) / 2 - 1).simplify()

\(presum(f)\) 就是 \(f\to F\)，\(uplevel(F)\) 就是 \(F\to h\) 的计算。大概意思就是，这个 Subs 函数就是函数复合，f.subs(x, i) 将 \(f(x)\) 换成 \(f(i)\)，F.subs(x, x * (x + 1) / 2 - 1) 就是 \(f(x)\) 变成 \(f(x(x+1)/2-1)\)。然后 Sum 就是求和，看格式，然后 simplify就是化简（但实际上简单不了多少，也可以换成 expand 或者 factor）。然后就可以 print 出来：

def trans(F):
    return presum(uplevel(F))

def trans2(f):
    return uplevel(presum(f))

f = x # 大 F
⁦print(f)
print(trans(f))
print(trans(trans(f)))
print(trans(trans(trans(f))))
# print(trans(trans(trans(trans(f)))))
f = x - x + 1 # 小 f，注意可能有一点神经，需要指定一下未知的元
print(f)
print(trans2(f))
print(trans2(trans2(f)))
print(trans2(trans2(trans2(f))))
# print(trans2(trans2(trans2(trans2(f)))))

然后要粘贴到 C++ 里面，需要把 python 的 ** 幂运算去掉。mint 是我们的高精度类型。

def custom_print(expr):
    s = str(expr.factor()) # 推荐输出前 factor（因式分解）
    for i in range(100, 1, -1):
        s = s.replace(f'x**{i}', '*'.join(['x'] * i))
    print(f'+[](mint x) -> mint {{ return {s}; }},')

将 print 全部换成 custom_print。

输出如下：

+[](mint x) -> mint { return x; },
+[](mint x) -> mint { return x*(x - 1)*(x + 4)/6; },
+[](mint x) -> mint { return x*(x - 1)*(5*x*x*x*x*x + 40*x*x*x*x + 131*x*x*x + 236*x*x - 44*x - 1024)/1680; },
+[](mint x) -> mint { return x*(x - 1)*(x + 4)*(429*x*x*x*x*x*x*x*x*x*x*x*x + 5148*x*x*x*x*x*x*x*x*x*x*x + 26697*x*x*x*x*x*x*x*x*x*x + 75636*x*x*x*x*x*x*x*x*x + 122031*x*x*x*x*x*x*x*x + 89604*x*x*x*x*x*x*x - 37373*x*x*x*x*x*x - 205140*x*x*x*x*x - 1140248*x*x*x*x - 4246656*x*x*x - 8781968*x*x - 10100160*x + 41554944)/276756480; },
+[](mint x) -> mint { return 1; },
+[](mint x) -> mint { return (x - 1)*(x + 2)/2; },
+[](mint x) -> mint { return (x - 1)*(x + 2)*(x*x + x - 4)*(x*x + x + 6)/48; },
+[](mint x) -> mint { return (x - 1)*(x + 2)*(x*x + x - 4)*(5*x*x*x*x*x*x*x*x*x*x + 25*x*x*x*x*x*x*x*x*x + 80*x*x*x*x*x*x*x*x + 170*x*x*x*x*x*x*x + 289*x*x*x*x*x*x + 377*x*x*x*x*x + 546*x*x*x*x + 612*x*x*x - 3864*x*x - 4128*x - 26880)/215040; },

+[](mint x) -> mint { return 1; } 是一个转型为函数指针的 Lambda 对象，其类型为 mint (*)(mint)。于是就可以将这 \(8\) 个函数存到代码里。

其它的代码不需要我教你怎么写了吧！

code

#include <bits/stdc++.h>
using namespace std;
#ifdef local
#define debug(...) fprintf(stderr, ##__va_args__)
#else
#define endl "\n"
#define debug(...) void(0)
#endif
// 省略一个高精度板子，见上
using mint = BigInt<9>;
mint operator*(int x, mint y) { return y * x; }
using LL = long long;
using FuncPtr = mint (*)(mint);
const FuncPtr F[] = {/*{{{*/
    /* 四个函数 */
}; /*}}}*/
const FuncPtr f[] = {/*{{{*/
    /* 四个函数 */
};/*}}}*/
constexpr int L = 1e6, N = L + 10;
mint q[N], preq[4][N];
int p[N];
mint P(mint n) {
  mint l = 0, r = mint(1) << (mint::n * 16 - 2), ans = 0;
  while (l <= r) {
    mint mid = (l + r) >> 1;
    if ((mid * (mid + 1) >> 1) <= n)
      ans = mid, l = mid + 1;
    else
      r = mid - 1;
  }
  return ans;
}
mint ns[110];
mint g(int c, int d) {
  if (ns[c] <= L) return preq[d][(int)ns[c]];
  return F[d](ns[c]) * g(c + 1, 0) - g(c + 1, d + 1);
}
int main() {
#ifndef LOCAL
  cin.tie(nullptr)->sync_with_stdio(false);
#endif
  q[1] = 1, p[1] = 1;
  int lst = 1;
  for (int i = 2; i <= L; i++) {
    if ((lst + 1) * (lst + 2) / 2 == i) ++lst;
    p[i] = lst;
    q[i] = q[i - 1] + q[lst];
  }
  for (int j = 0; j < 4; j++) {
    for (int i = 1; i <= L; i++) {
      preq[j][i] = preq[j][i - 1] + f[j](i) * q[p[i]];
    }
  }
  int t;
  cin >> t;
  while (t--) {
    cin >> ns[0];
    for (int i = 1; i <= 4; i++) ns[i] = P(ns[i - 1]);
    cout << g(0, 0) << endl;
  }
  return 0;
}

posted @ 2024-12-24 20:38 caijianhong 阅读(131) 评论(0) 收藏举报

刷新页面返回顶部