SVPWM - 学习笔记
SVPWM - 学习笔记
前提预备 - 数学知识
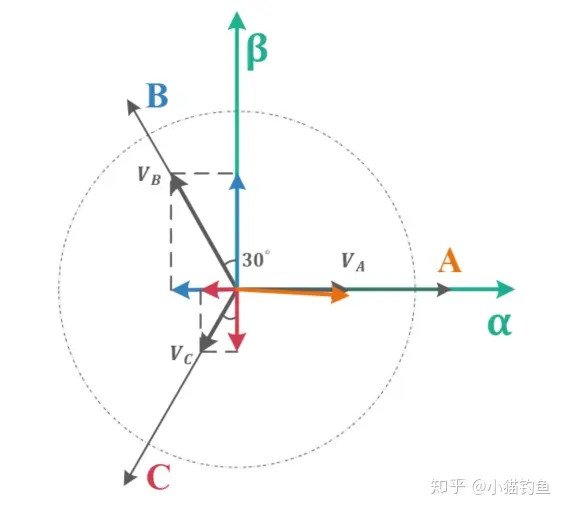
Clack变换
实际上clack变换就是坐标系的变换,再直白点,就是将三个角度互为120度的向量变成两个角度互为90度的向量
\[\left[ \begin{array}{c} V_{\alpha}\\ V_{\beta}\\ \end{array} \right] =\left[ \begin{array}{c} V_A-V_B\cos \left( 60^{\circ} \right) -V_C\cos \left( 60^{\circ} \right)\\ V_B\cos \left( 30^{\circ} \right) -V_C\cos \left( 30^{\circ} \right)\\ \end{array} \right] =\left[ \begin{matrix} 1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ \end{matrix} \right] \left[ \begin{array}{c} V_A\\ V_B\\ V_C\\ \end{array} \right]
\]
\[\begin{aligned} V_{\delta}&=V_{\alpha}+jV_{\beta}=V_A+V_B\cdot e^{j\cdot 120^{\circ}}+V_c\cdot e^{-j\cdot 120^{\circ}} \\ &=V_A+V_B\cdot \left[ \cos \left( 120^{\circ} \right) +j\sin \left( 120^{\circ} \right) \right] +V_C\cdot \left[ \cos \left( 120^{\circ} \right) -j\sin \left( 120^{\circ} \right) \right] \\ &=V_A-\frac{1}{2}V_B-\frac{1}{2}V_C+j\frac{\sqrt{3}}{2}\left( V_B-V_C \right) \\ &\Rightarrow \\ V_{\alpha}&=V_A-\frac{1}{2}V_B-\frac{1}{2}V_C \\ V_{\beta}&=\frac{\sqrt{3}}{2}\left( V_B-V_C \right) \end{aligned}
\]
\[\left[ \begin{array}{c} V_{\alpha}\\ V_{\beta}\\ \end{array} \right] =\frac{2}{3}\left[ \begin{matrix} 1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ \end{matrix} \right] \left[ \begin{array}{c} V_A\\ V_B\\ V_C\\ \end{array} \right]
\]
上面的式子是等幅值变换,也就是在前面乘了2/3
记
\[T_{3s-2s}=\frac{2}{3}\left[ \begin{matrix} 1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ \end{matrix} \right]
\]
T_{3s-2s}称为Clark变换,它是Edith Clarke 最先针对交流系统电路分析提出的,现在被广泛的应用于三相逆变器的控制中。
等幅值Clark变换与等功率Clark变换可以统一表示为:
\[T_{3s-2s}=k\cdot \left[ \begin{matrix} 1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ \end{matrix} \right]
\]
其中 K=2/3 为等幅值变换, k=sqrt(2/3) 为等功率变换。
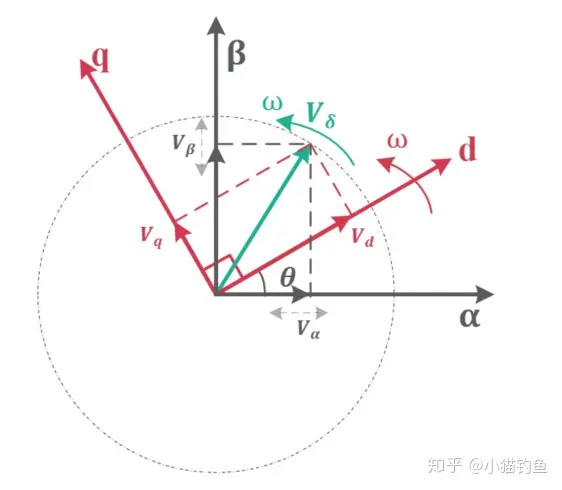
Park变换
Park变换实际上是一个旋转的直角坐标系,原先坐标系的两个向量投影到新的坐标系上

\[\begin{aligned} V_{\delta}&=V_{\alpha}+jV_{\beta}=\left( V_d+jV_q \right) \cdot e^{j\theta} \\ &\Rightarrow \\ V_d+jV_q&=\left( V_{\alpha}+jV_{\beta} \right) \cdot e^{-j\theta} \\ &=\left( V_{\alpha}+jV_{\beta} \right) \cdot \left( \cos \left( \theta \right) -j\sin \left( \theta \right) \right) \\ &=V_{\alpha}\cos \left( \theta \right) +V_{\beta}\sin \left( \theta \right) +j\left[ -V_{\alpha}\sin \left( \theta \right) +V_{\beta}\cos \left( \theta \right) \right] \\ &\Rightarrow \\ \left[ \begin{array}{c} V_d\\ V_q\\ \end{array} \right] &=\left[ \begin{array}{c} V_{\alpha}\cos \left( \theta \right) +V_{\beta}\sin \left( \theta \right)\\ -V_{\alpha}\sin \left( \theta \right) +V_{\beta}\cos \left( \theta \right)\\ \end{array} \right] =\left[ \begin{matrix} \cos \left( \theta \right)& \sin \left( \theta \right)\\ -\sin \left( \theta \right)& \cos \left( \theta \right)\\ \end{matrix} \right] \left[ \begin{array}{c} V_{\alpha}\\ V_{\beta}\\ \end{array} \right] \end{aligned}
\]
其中
\[T_{2s-2r}=\left[ \begin{matrix} \cos \left( \theta \right)& \sin \left( \theta \right)\\ -\sin \left( \theta \right)& \cos \left( \theta \right)\\ \end{matrix} \right]
\]
前提预备 - 电机知识
三相电压瞬时表达式

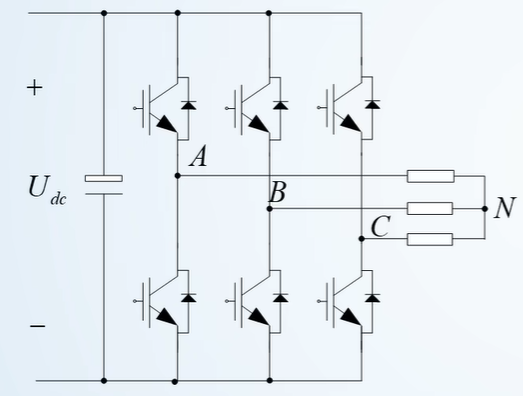
两电平控制器 - 电路结构
其实就是三个完整的H桥
每一路都有两个开关来限制电流的流向
注意:每一路的两个开关不能同时打开,不然就短路了
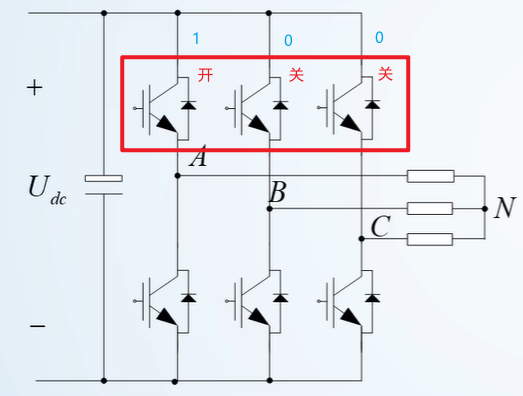
H桥开关情况和电流流向
当上面的开关开启时,下面的开关应该关闭;我们以上面的开关为例,当上面的A路开关打开时,我们称A路为1,否则为0
关于等幅值变换:等赋值变换在克拉克变换当中较为常见,克拉克变化是将三相电压/电流变换为两相来进行处理,在转换的过程当中会出现原本为1的数值变成了原来的3/2,幅值并不相同,原本的电机三相幅值应该为单位1,而进行了克拉克变换之后幅值变成了3/2,不利于信号的调制,所以应该在后面的结果乘上2/3
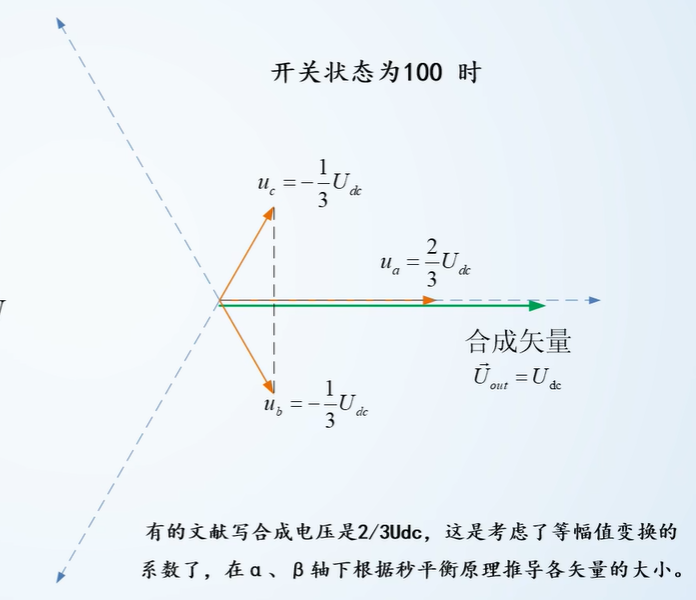
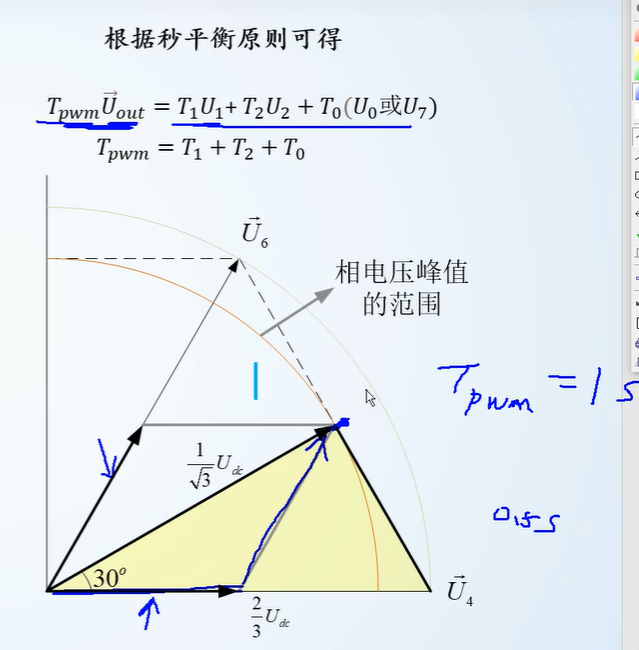
秒平衡原理
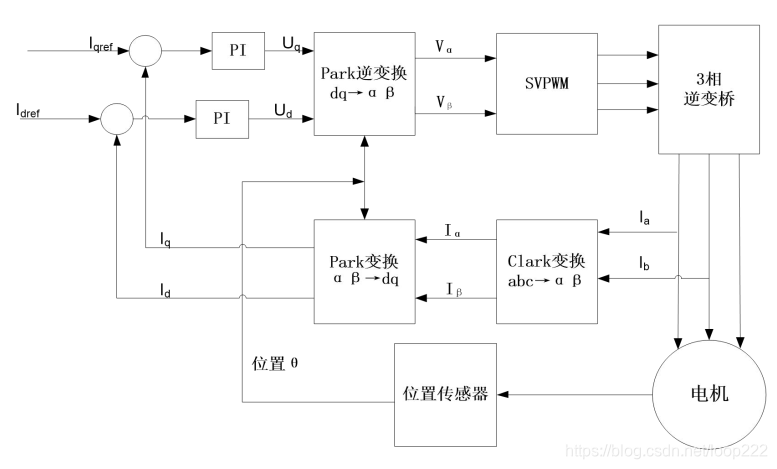
SVPWM - 在SimpleFOC上的应用路径
无感FOC
有感FOC
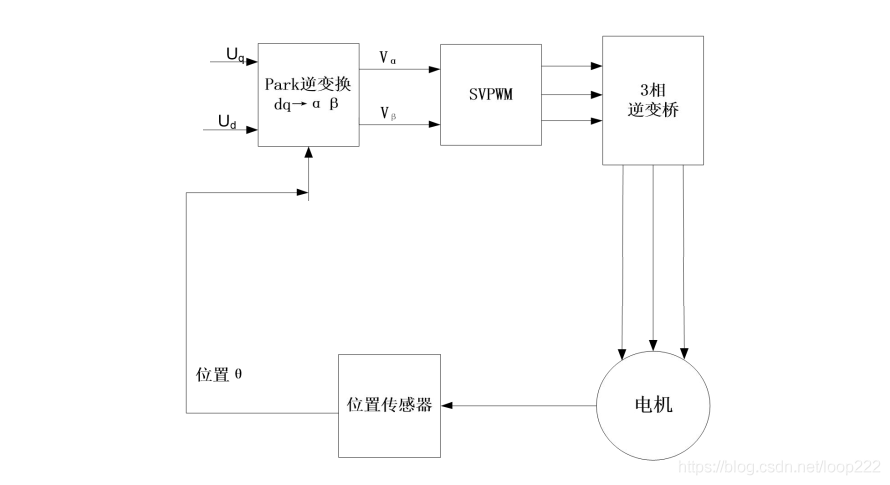
可见SVPWM是在接收Park逆变换下的两个量下,转化后输出ABC三个量给PWM
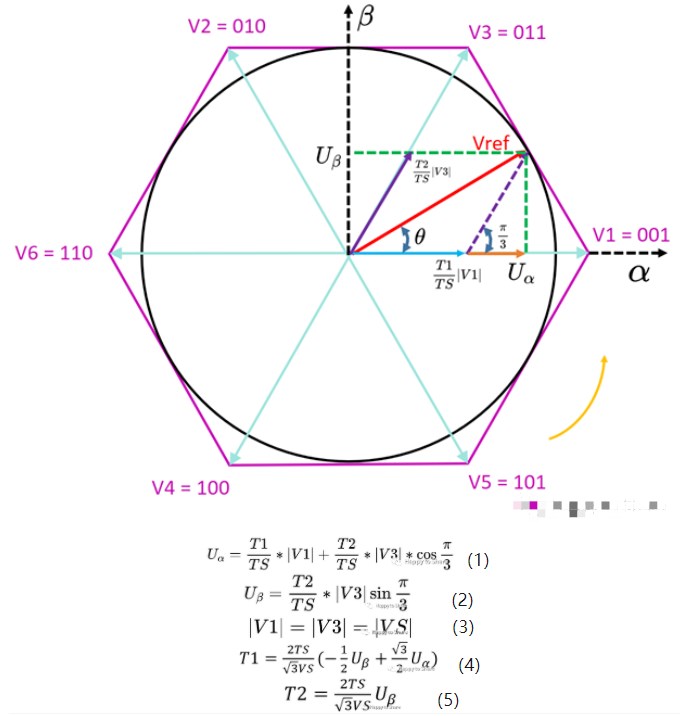
SVPWM - 堆导
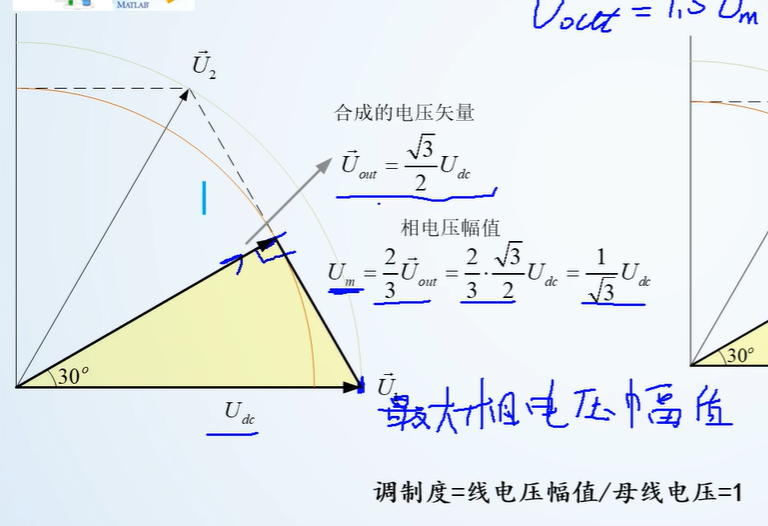
最大相电压幅值
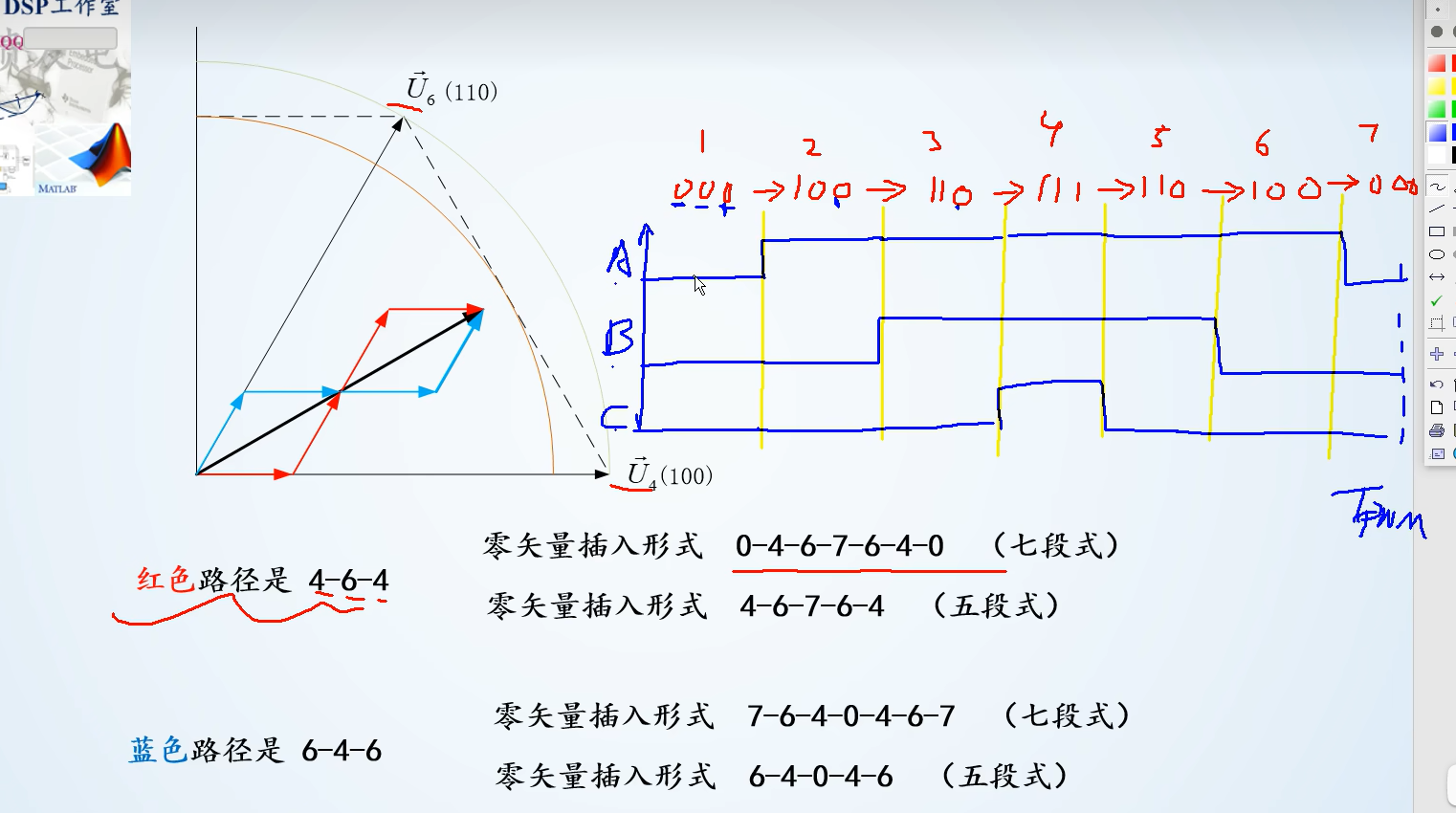
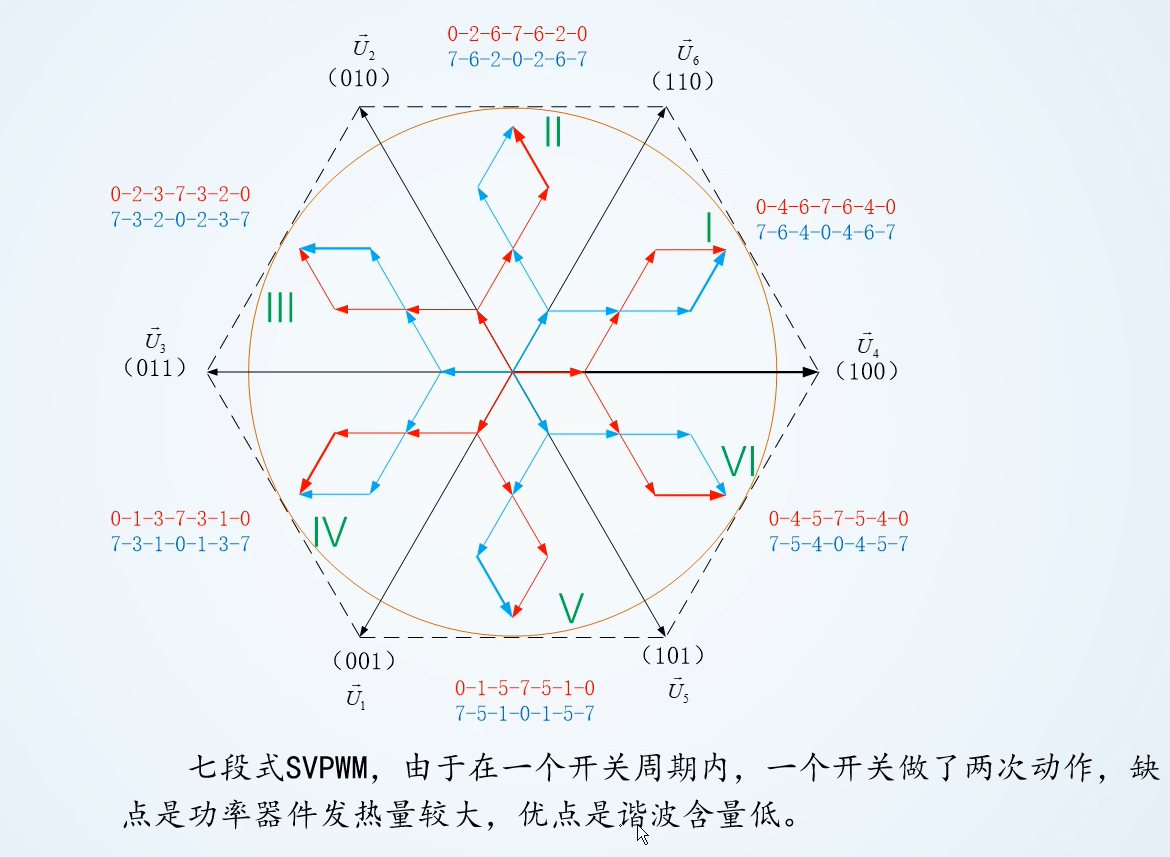
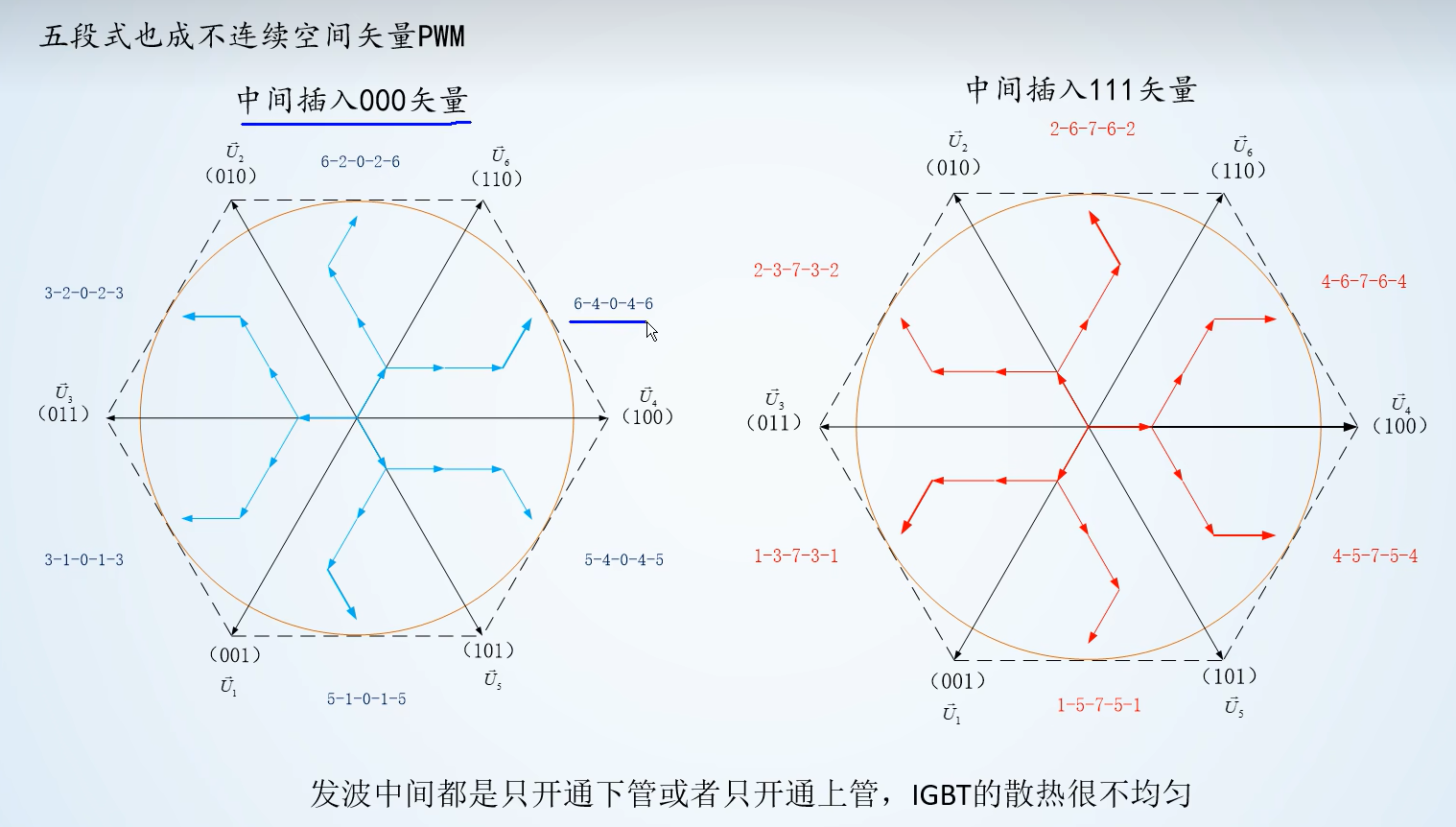
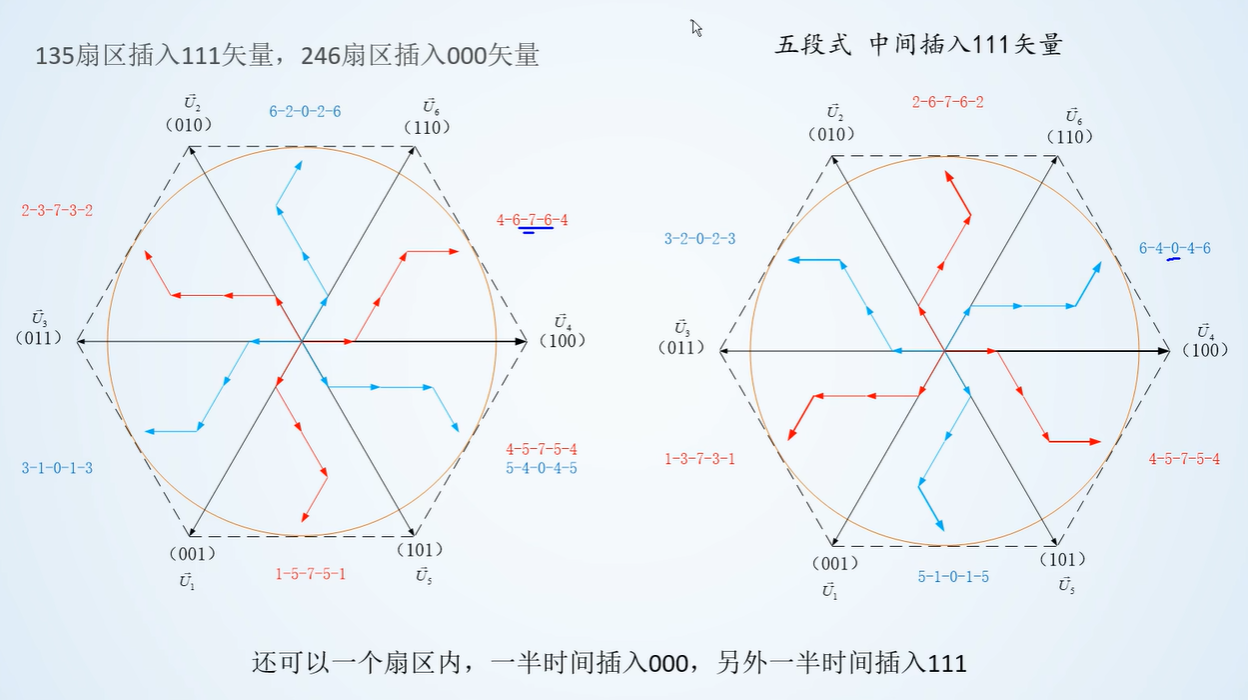
五段式和七段式
七段式
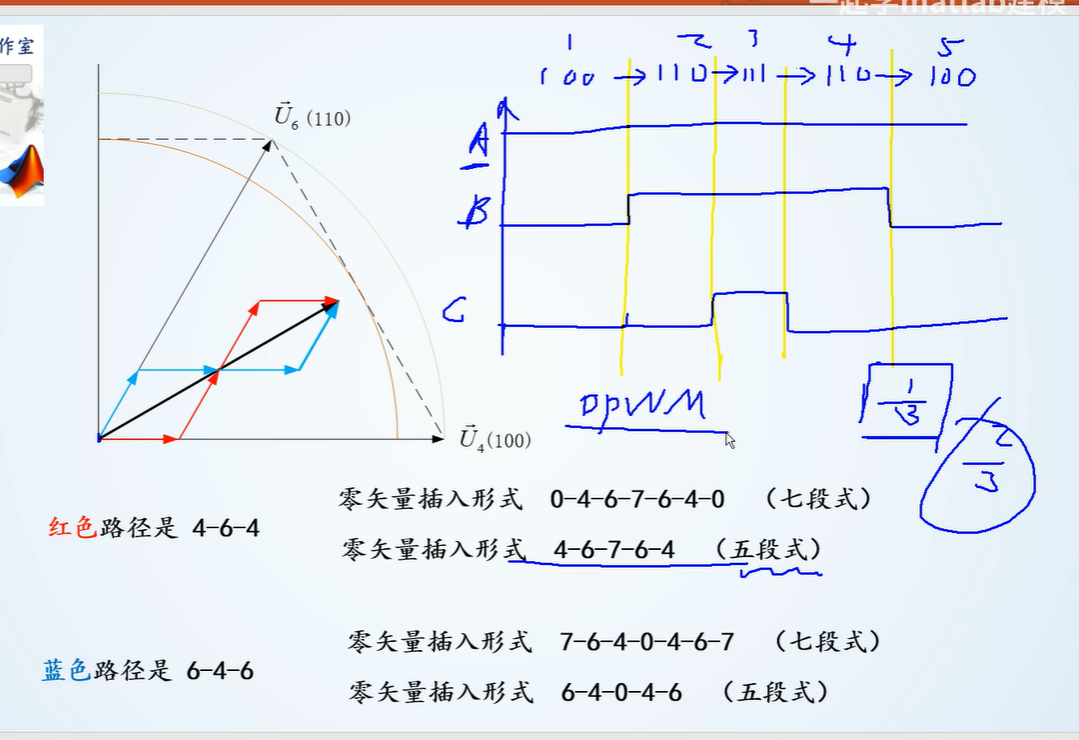
五段式(DPWM 不连续)

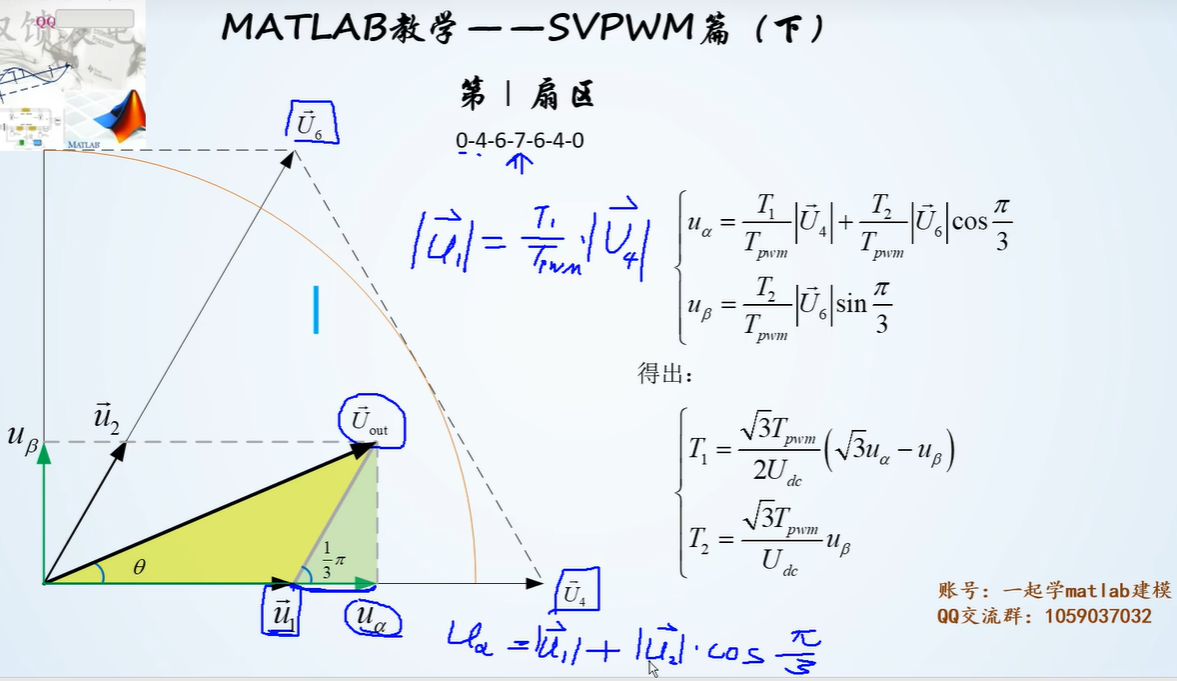
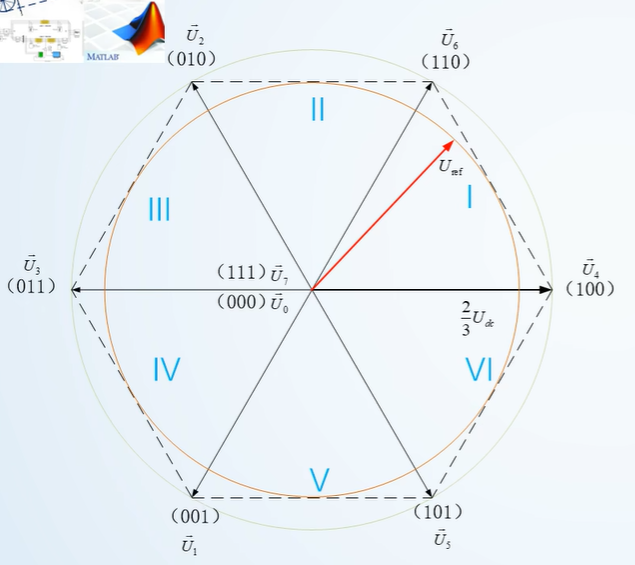
扇区判断
SVPWM的输入是两个量



 浙公网安备 33010602011771号
浙公网安备 33010602011771号