SimpleBGC IMU-AHRS部分解析
SimpleBGC IMU-AHRS部分解析
IMU部分解析
航姿参考系统初始化 - MargAHRSinit
三维旋转:欧拉角、四元数、旋转矩阵、轴角之间的转换 - 知乎 (zhihu.com)
四元数和欧拉角之间的转换 - 维基百科,自由的百科全书 (wikipedia.org)
四元数和欧拉角 - love _荣 - 博客园 (cnblogs.com)
//==================================================================================================== // Initialization //==================================================================================================== // 航姿参考系统初始化 void MargAHRSinit(float ax, float ay, float az, float mx, float my, float mz) { float initialRoll, initialPitch; float cosRoll, sinRoll, cosPitch, sinPitch; float magX, magY; float initialHdg, cosHeading, sinHeading; // 使用加速度数据计算欧拉角 ,滚转角和俯仰角 initialRoll = atan2(-ay, -az); initialPitch = atan2(ax, -az); // 对欧拉角进行余弦和正弦计算,分别把计算结果保存下来 cosRoll = cosf(initialRoll); sinRoll = sinf(initialRoll); cosPitch = cosf(initialPitch); sinPitch = sinf(initialPitch); magX = 1.0f; // HJI mx * cosPitch + my * sinRoll * sinPitch + mz * cosRoll * sinPitch; magY = 0.0f; // HJI my * cosRoll - mz * sinRoll; initialHdg = atan2f(-magY, magX); // 解算航向角 cosRoll = cosf(initialRoll * 0.5f); sinRoll = sinf(initialRoll * 0.5f); cosPitch = cosf(initialPitch * 0.5f); sinPitch = sinf(initialPitch * 0.5f); cosHeading = cosf(initialHdg * 0.5f); sinHeading = sinf(initialHdg * 0.5f); // 得到四元数 q0 = cosRoll * cosPitch * cosHeading + sinRoll * sinPitch * sinHeading; q1 = sinRoll * cosPitch * cosHeading - cosRoll * sinPitch * sinHeading; q2 = cosRoll * sinPitch * cosHeading + sinRoll * cosPitch * sinHeading; q3 = cosRoll * cosPitch * sinHeading - sinRoll * sinPitch * cosHeading; // 把计算参考方向用到的值先都计算好,减少重复计算,因为MargAHRSupdate函数里面要用到。 // auxillary variables to reduce number of repeated operations, for 1st pass q0q0 = q0 * q0; q0q1 = q0 * q1; q0q2 = q0 * q2; q0q3 = q0 * q3; q1q1 = q1 * q1; q1q2 = q1 * q2; q1q3 = q1 * q3; q2q2 = q2 * q2; q2q3 = q2 * q3; q3q3 = q3 * q3; }
流程
- 使用加速度计计算欧拉角
- 通过欧拉角计算四元数
加速度数值置信度计算 - calculateAccConfidence
对于置信度的理解,以及IMU使用加速度传感器/陀螺仪进行姿态解算的理解
来自你的消息:
void calculateAccConfidence(float accMag) { // G.K. Egan (C) computes confidence in accelerometers when // aircraft is being accelerated over and above that due to gravity static float accMagP = 1.0f; accMag /= accelOneG; // HJI Added to convert MPS^2 to G's accMag = HardFilter(accMagP, accMag); accMagP = accMag; accConfidence = constrain(1.0f - (accConfidenceDecay * sqrt(fabs(accMag - 1.0f))), 0.0f, 1.0f); }这串代码是计算IMU的加速度传感器的置信度,你解析一下代码,然后告诉我置信度的数学计算公式,置信度对于加速度传感器数值的变化关系
来自 ChatGPT 的消息:
这段代码用于计算加速度传感器的置信度。让我逐步解析代码并解释置信度的数学计算公式以及它与加速度传感器数值的变化关系。
首先,代码中定义了一个静态变量
accMagP,初始值为1.0。这个变量用于存储上一次计算得到的加速度的幅值。接下来,
accMag被除以accelOneG,这个值可能是一个常数,用于将加速度转换为以重力加速度为单位的数值。这个操作的目的是将加速度值转换为以 "G" 为单位的数值。然后,
accMag被传递给HardFilter函数进行滤波处理。这个函数可能是一个自定义的滤波器,用于平滑加速度数据。接着,
accMag的值被赋给accMagP,以便在下一次计算中使用。最后,置信度被计算为
1.0 - (accConfidenceDecay * sqrt(fabs(accMag - 1.0f))),并被限制在范围 [0.0, 1.0] 内。这个公式的含义如下:
fabs(accMag - 1.0f):计算当前加速度值与标准重力加速度之间的差值的绝对值。sqrt(fabs(accMag - 1.0f)):对差值的绝对值进行平方根运算。accConfidenceDecay:一个常数,用于调整置信度的衰减速度。accConfidenceDecay * sqrt(fabs(accMag - 1.0f)):计算置信度的衰减量。1.0 - (accConfidenceDecay * sqrt(fabs(accMag - 1.0f))):将衰减量从1中减去,得到最终的置信度值。因此,当加速度传感器的数值与标准重力加速度之间的差距越小,置信度越高。当差距较大时,置信度会逐渐降低。衰减速度由
accConfidenceDecay控制。来自你的消息:
置信度的意义是什么,有什么作用,如果不使用置信度会怎么样?
如果飞机处于加速状态,置信度会IMU姿态解算造成什么影响来自 ChatGPT 的消息:
置信度在这里表示对加速度传感器测量值的信任程度或可靠性。它用于衡量加速度传感器测量值与实际加速度之间的一致性。置信度的作用是在姿态解算或其他相关算法中,根据加速度传感器的可靠性来调整其权重或影响结果的可靠性。
如果不使用置信度或忽略加速度传感器的可靠性,可能会导致以下问题:
姿态解算的不准确性:加速度传感器在飞机加速状态下可能会受到其他因素的干扰,例如飞机的振动、外部力的影响等。如果不考虑加速度传感器的置信度,这些干扰可能导致姿态解算的不准确性,从而影响飞机的姿态估计。
不稳定的结果:没有考虑置信度可能导致加速度传感器的不可靠测量值对结果产生过大的影响。这可能导致结果的不稳定性,尤其是在飞机加速状态下,加速度传感器的测量值可能会偏离实际加速度,进而影响姿态解算的稳定性。
通过使用置信度,可以根据加速度传感器的可靠性对测量值进行加权或调整,从而提高姿态解算的准确性和稳定性。当飞机处于加速状态时,如果置信度较低,姿态解算算法可以减小加速度传感器的权重,以减少其对姿态估计的影响,从而更好地适应飞机的实际状态。这样可以降低因加速度传感器测量误差而引起的姿态误差,并提高姿态解算的鲁棒性和可靠性。
来自你的消息:
这是否意味着IMU使用加速度传感器计算飞机姿态时,参照的是IMU在静止状态下的情况,也就是说在飞机加速状态下,加速度传感器的数值对飞机姿态的计算的权值应该降低,此时使用加速度传感器计算飞机姿态是可靠的。如果是这样的话,在飞机加速状态下,有没有什么更好的方法
来自 ChatGPT 的消息:
是的,您的理解是正确的。在飞机加速状态下,加速度传感器的数值对于计算飞机姿态的权重应该降低,因为加速度传感器在飞机加速时可能会受到其他因素的干扰,从而导致测量值的不准确性。
除了加速度传感器,惯性测量单元(IMU)通常还包括陀螺仪和磁力计等传感器。这些传感器可以提供陀螺仪角速度和磁力计磁场信息,用于更准确地计算飞机的姿态。
在飞机加速状态下,可以考虑以下方法来改进姿态估计的可靠性:
使用陀螺仪数据:陀螺仪可以提供飞机的角速度信息,通过积分这些角速度值,可以估计飞机的姿态。相对于加速度传感器,陀螺仪对加速度的干扰较小,因此在飞机加速状态下,可以更依赖陀螺仪数据来计算姿态。
融合多个传感器数据:通过使用传感器融合算法,如卡尔曼滤波器或扩展卡尔曼滤波器,将加速度传感器、陀螺仪和磁力计等多个传感器的数据进行融合,可以更准确地计算飞机的姿态。这样可以利用各个传感器的优势,并减少对单个传感器的依赖。
使用额外的传感器或信息:除了IMU传感器外,可以考虑使用其他传感器或信息来辅助姿态估计。例如,可以使用GPS数据、视觉传感器或地面参考点等来提供更准确的姿态信息。
综上所述,通过结合陀螺仪数据、传感器融合算法以及其他辅助传感器或信息,可以提高在飞机加速状态下的姿态估计的可靠性和精度。
来自你的消息:
如果飞机一直处于加速状态下,加速度传感器的权值降低,也就是陀螺仪数据的权值变高,在持续加速一段时间后,飞机的姿态会发送偏移吗?
来自 ChatGPT 的消息:
如果飞机一直处于加速状态下,加速度传感器的权值降低、陀螺仪数据的权值增加,会导致飞机姿态的估计更加依赖于陀螺仪数据。在持续加速一段时间后,由于加速度传感器的权值降低,加速度传感器的测量误差对姿态估计的影响减小,而陀螺仪的角速度数据则起到更大的作用。
在这种情况下,如果陀螺仪的角速度数据准确且稳定,飞机的姿态估计可能会相对稳定。然而,如果陀螺仪存在漂移或噪声等问题,姿态估计可能会受到影响并发生偏移。
陀螺仪存在漂移是一个常见的问题,特别是在长时间的运行中。漂移是指陀螺仪输出的角速度存在持续的误差累积,导致姿态估计的偏移。为了解决这个问题,通常需要使用陀螺仪校准技术,例如零偏校准或姿态校准算法,以减小或校正陀螺仪的漂移误差。
另外,持续加速状态下的姿态估计还可能受到其他因素的影响,例如飞机的振动、外部干扰等。这些因素可能会对陀螺仪和加速度传感器的数据产生影响,进而影响姿态估计的准确性和稳定性。
因此,在飞机持续加速状态下,姿态估计的准确性和稳定性仍然需要综合考虑多个因素,并采取适当的校准和滤波技术,以确保姿态估计的精度和可靠性。
置信度计算相关代码
//From config.c - Line 7
void readEEPROM(void)
{
// Read flash
memcpy(&eepromConfig, (char *)FLASH_WRITE_EEPROM_CONFIG_ADDR, sizeof(eepromConfig_t));
accConfidenceDecay = 1.0f / sqrt(eepromConfig.accelCutoff);
mechanical2electricalDegrees[ROLL ] = eepromConfig.rollMotorPoles / 2.0f;
mechanical2electricalDegrees[PITCH] = eepromConfig.pitchMotorPoles / 2.0f;
mechanical2electricalDegrees[YAW ] = eepromConfig.yawMotorPoles / 2.0f;
electrical2mechanicalDegrees[ROLL ] = 1.0f / mechanical2electricalDegrees[ROLL ];
electrical2mechanicalDegrees[PITCH] = 1.0f / mechanical2electricalDegrees[PITCH];
electrical2mechanicalDegrees[YAW ] = 1.0f / mechanical2electricalDegrees[YAW ];
}
//From MargAHRS.c
float accConfidenceDecay = 0.0f;
float accConfidence = 1.0f;
#define HardFilter(O, N) ((O)*0.9f + (N)*0.1f)
void calculateAccConfidence(float accMag)
{
// G.K. Egan (C) computes confidence in accelerometers when
// aircraft is being accelerated over and above that due to gravity
static float accMagP = 1.0f;
accMag /= accelOneG; // HJI Added to convert MPS^2 to G's
accMag = HardFilter(accMagP, accMag);
accMagP = accMag;
accConfidence = constrain(1.0f - (accConfidenceDecay * sqrt(fabs(accMag - 1.0f))), 0.0f, 1.0f);
}
//calculateAccConfidence被调用处
//航姿参考系统更新
//void MargAHRSupdate(float gx, float gy, float gz,
// float ax, float ay, float az,
// float mx, float my, float mz,
// uint8_t magDataUpdate, float dt)
calculateAccConfidence(norm); // 由于处于运动状态,所有要计算加速度数据归一化后的可信度
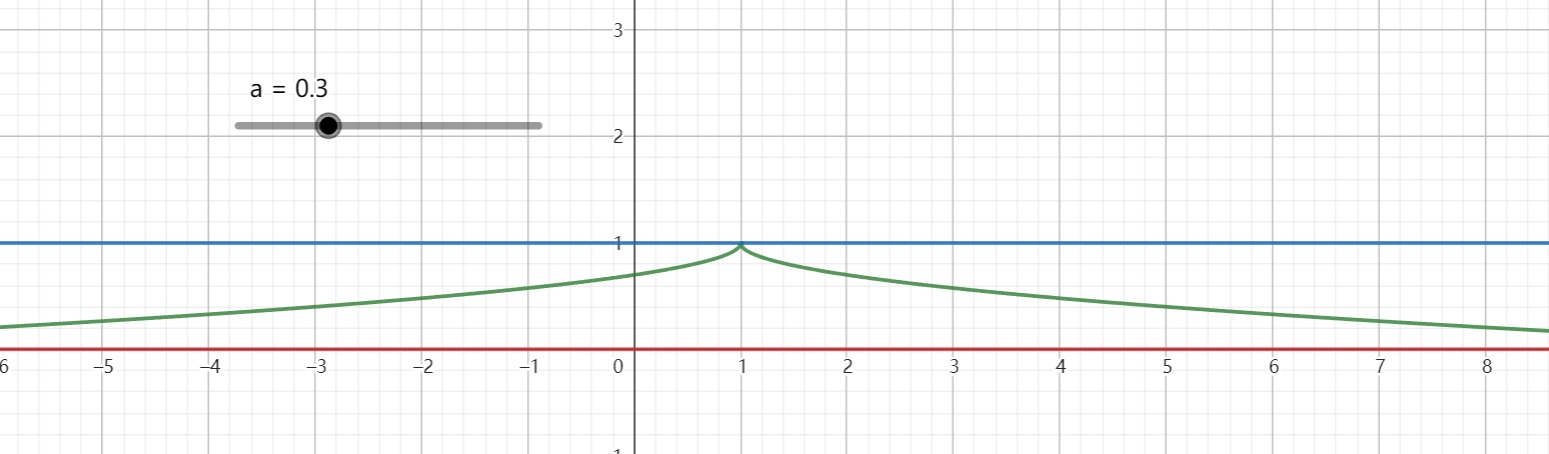
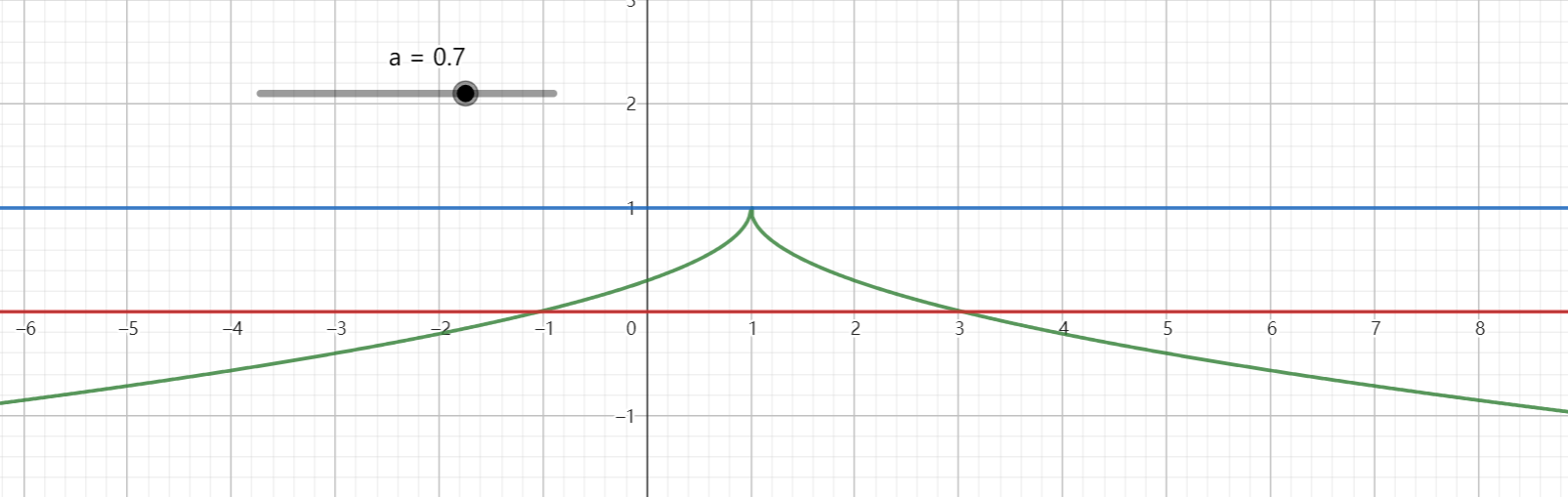
置信度的初始化设置
- 截至数值设置 - accConfidenceDecay
- 该数值越靠近0,截至范围越大;越靠近1,截至范围越小
![image-20231106165743022]()
![image-20231106165752806]()
置信度的作用对象
kpAcc_a = eepromConfig.KpAcc_a * accConfidence; // 加速度比例系数 * 可信度
kpAcc_b = eepromConfig.KpAcc_b * accConfidence; // 加速度比例系数 * 可信度
kpAcc_c = eepromConfig.KpAcc_c * accConfidence; // 加速度比例系数 * 可信度
kiAcc = eepromConfig.KiAcc * accConfidence; // 加速度积分系数 * 可信度
置信度作用与加速度比例系数
置信度的使用注意事项
由于置信度的直接作用对象是加速度的比例/积分系数,意味着置信度作用下的基数是PID系数,因此PID的参数是影响表现效果的关键。若PID很大,陀螺仪数据收敛过快,而置信度的作用不明显,输出的欧拉角仍然跟随着加速度变化。
置信度的意义
当使用PID作为互补滤波的控制算法时,置信度可对PID的作用/增益参数进行调整,根据加速度计整体加速度的变化/与1G的变化得出置信度并对PID参数进行衰减,减缓陀螺仪数据收敛的速度。从结果上看,置信度实际上是 加速度计收敛期望 相对 1G加速度 的滤波。
航姿参考系统更新 - MargAHRSupdate
Math相关:
叉积 - 维基百科,自由的百科全书 (wikipedia.org)
关于方向矩阵:
来自你的消息:
// estimated direction of gravity (v) vx = 2.0f * (q1q3 - q0q2); // 计算方向余弦矩阵 vy = 2.0f * (q0q1 + q2q3); vz = q0q0 - q1q1 - q2q2 + q3q3;这个是航姿参考系统更新中的,q0-q3是四元数,这个计算是什么意思,原理是什么
来自 ChatGPT 的消息:
这段代码是用于在航姿参考系统中更新估计的重力方向(v)的代码片段。其中,q0、q1、q2和q3分别是四元数的四个分量。
这段代码实际上是根据四元数来计算方向余弦矩阵(Direction Cosine Matrix),也称为旋转矩阵。方向余弦矩阵是一个3x3的矩阵,用于描述物体在三维空间中的旋转。
具体来说,这段代码计算了重力方向在航姿参考系统中的估计值(vx、vy和vz)。下面是计算的原理:
首先,根据四元数的定义,将四元数的分量代入计算公式中:
vx = 2.0f * (q1q3 - q0q2)
vy = 2.0f * (q0q1 + q2q3)
vz = q0q0 - q1q1 - q2q2 + q3q3这些计算实际上是通过将四元数转换为方向余弦矩阵来得到重力方向的估计。方向余弦矩阵描述了从一个坐标系到另一个坐标系的旋转关系。
在这个代码片段中,通过将四元数的分量代入方向余弦矩阵的计算公式,可以得到重力方向的估计值。
这个计算的原理是基于四元数和方向余弦矩阵之间的关系,通过将四元数转换为方向余弦矩阵,可以得到重力方向在航姿参考系统中的估计值。这个估计值可以用于姿态估计、导航和控制等应用中。
来自你的消息:
方向余弦矩阵是不是说载体坐标系的每个轴当成一个向量,三个轴有三个向量,请问每个向量的组成是什么?方向余弦矩阵是不是有九个数组成,欧拉角由三个数组成
来自 ChatGPT 的消息:
是的,方向余弦矩阵描述了从一个坐标系到另一个坐标系的旋转关系。在航姿参考系统中,通常使用的是载体坐标系(也称为机体坐标系)和地理坐标系(通常是地球坐标系)。
在方向余弦矩阵中,每个轴都被表示为一个向量。对于载体坐标系,通常选择三个轴:X轴、Y轴和Z轴。这三个轴的向量组成如下:
X轴向量:[D11, D21, D31]
Y轴向量:[D12, D22, D32]
Z轴向量:[D13, D23, D33]其中,D11、D21、D31表示X轴向量的分量,D12、D22、D32表示Y轴向量的分量,D13、D23、D33表示Z轴向量的分量。
方向余弦矩阵是一个3x3的矩阵,由这三个向量组成。因此,方向余弦矩阵总共有9个元素。
与此不同,欧拉角是一种常用的姿态表示方法,它由三个角度组成,通常是滚转角(Roll)、俯仰角(Pitch)和航向角(Yaw)。这三个角度可以用来描述载体坐标系相对于地理坐标系的旋转。
来自你的消息:
从信息量上看,欧拉角是三个值组成,其几何意义是不是三个角度对应的三轴旋转,旋转顺序也是要提供的
这样看的话,如果把欧拉角的旋转顺序算上其信息量是不是有六个值,而方向余弦矩阵有9个值来自 ChatGPT 的消息:
是的,欧拉角由三个角度组成,通常表示为 (Roll, Pitch, Yaw)。每个角度对应于载体坐标系绕着参考坐标系的三个轴旋转的角度。
欧拉角的几何意义是通过一系列旋转将一个坐标系转换到另一个坐标系。旋转顺序非常重要,因为不同的旋转顺序会导致不同的姿态变换结果。常见的旋转顺序有三个:XYZ、ZYX和YXZ。例如,XYZ顺序表示先绕X轴旋转,然后绕Y轴旋转,最后绕Z轴旋转。
根据旋转顺序的不同,欧拉角的信息量可以有所不同。如果考虑旋转顺序,欧拉角的信息量可以表示为六个值。这六个值可以完全描述姿态的旋转过程。
而方向余弦矩阵是一个3x3的矩阵,共有9个值。这些值表示了载体坐标系相对于参考坐标系的旋转关系。方向余弦矩阵提供了更直接的旋转表示,而无需考虑旋转顺序的问题。
总结起来,欧拉角和方向余弦矩阵都可以用来表示姿态的旋转,但在信息量上有所不同。欧拉角需要提供旋转顺序,因此有六个值,而方向余弦矩阵直接提供了九个值来描述旋转关系。
来自你的消息:
方向余弦矩阵的三个轴的向量是孤立的吗,会不会出现三个向量不相互正交垂直的情况
来自 ChatGPT 的消息:
方向余弦矩阵的三个轴向量是相互正交且垂直的,它们构成了一个正交矩阵。正交矩阵的定义是指矩阵的列向量(或行向量)两两之间都正交(垂直)且归一化(长度为1)。
在方向余弦矩阵中,每个轴向量都表示载体坐标系的一个轴,它们之间是相互独立的。由于方向余弦矩阵是用来描述旋转关系的,这三个轴向量必须满足以下条件:
正交性:每两个轴向量之间都正交(垂直),即内积为0。例如,X轴向量与Y轴向量的内积为0,X轴向量与Z轴向量的内积为0,Y轴向量与Z轴向量的内积为0。
归一性:每个轴向量的长度为1,即每个轴向量的模为1。这是为了确保方向余弦矩阵描述的旋转是单位旋转。
当满足上述条件时,方向余弦矩阵的三个轴向量就是相互正交且垂直的,它们定义了一个正交坐标系。这种正交性保证了方向余弦矩阵的有效性和可靠性,使其成为一种常用的姿态表示方法。
//====================================================================================================
// Function
//====================================================================================================
// 航姿参考系统更新
void MargAHRSupdate(float gx, float gy, float gz,
float ax, float ay, float az,
float mx, float my, float mz,
uint8_t magDataUpdate, float dt)
{
float norm, normR;
float hx, hy, hz, bx, bz;
float vx, vy, vz, wx, wy, wz;
float q0i, q1i, q2i, q3i;
//-------------------------------------------
if ((MargAHRSinitialized == false)) // HJI && (magDataUpdate == true))
{
// 如果航姿参考系统参数还没有初始化过,那么执行AHRS初始化
MargAHRSinit(ax, ay, az, mx, my, mz);
MargAHRSinitialized = true; // 标记航姿参考系统参数已经初始化过
}
//-------------------------------------------
if (MargAHRSinitialized == true) // 如果航姿参考系统参数已经初始化过
{
halfT = dt * 0.5f; // 半周期,求解四元数微分方程时用得到。
norm = sqrt(SQR(ax) + SQR(ay) + SQR(az)); // 加速度归一化
if (norm != 0.0f) // 如果归一化后的模等于0 ,那么说明加速度数据或者传感器不正常,正常情况下 归一化后的结果恒等于 1.0 ,这是重点。
{
calculateAccConfidence(norm); // 由于处于运动状态,所有要计算加速度数据归一化后的可信度
kpAcc = eepromConfig.KpAcc * accConfidence; // 加速度比例系数 * 可信度
kiAcc = eepromConfig.KiAcc * accConfidence; // 加速度积分系数 * 可信度
normR = 1.0f / norm; // 加速度归一化
ax *= normR;
ay *= normR;
az *= normR;
// estimated direction of gravity (v)
vx = 2.0f * (q1q3 - q0q2); // 计算方向余弦矩阵
vy = 2.0f * (q0q1 + q2q3);
vz = q0q0 - q1q1 - q2q2 + q3q3;
// error is sum of cross product between reference direction
// of fields and direction measured by sensors
// 误差是由传感器测量的参考方向与方向之间的叉积,由此
// 得到一个误差向量,通过这个误差向量来修正陀螺仪数据。
exAcc = vy * az - vz * ay;
eyAcc = vz * ax - vx * az;
ezAcc = vx * ay - vy * ax;
gx += exAcc * kpAcc; // 比例增益控制加速度计的收敛速度
gy += eyAcc * kpAcc;
gz += ezAcc * kpAcc;
if (kiAcc > 0.0f) // 用积分增益控制陀螺仪的偏差收敛速率
{
exAccInt += exAcc * kiAcc;
eyAccInt += eyAcc * kiAcc;
ezAccInt += ezAcc * kiAcc;
gx += exAccInt;
gy += eyAccInt;
gz += ezAccInt;
}
}
//-------------------------------------------
norm = sqrt(SQR(mx) + SQR(my) + SQR(mz)); // 三轴磁力计归一化
if ((magDataUpdate == true) && (norm != 0.0f)) // 如果入口参数magDataUpdate == true并且归一化的结果norm不是0,才对磁力计数据进行更新计算
{
normR = 1.0f / norm; // 三轴磁场归一化
mx *= normR;
my *= normR;
mz *= normR;
// compute reference direction of flux
// 计算参考方向
hx = 2.0f * (mx * (0.5f - q2q2 - q3q3) + my * (q1q2 - q0q3) + mz * (q1q3 + q0q2));
hy = 2.0f * (mx * (q1q2 + q0q3) + my * (0.5f - q1q1 - q3q3) + mz * (q2q3 - q0q1));
hz = 2.0f * (mx * (q1q3 - q0q2) + my * (q2q3 + q0q1) + mz * (0.5f - q1q1 - q2q2));
bx = sqrt((hx * hx) + (hy * hy));
bz = hz;
// estimated direction of flux (w)
// 根据参考方向估计云台机体方向
wx = 2.0f * (bx * (0.5f - q2q2 - q3q3) + bz * (q1q3 - q0q2));
wy = 2.0f * (bx * (q1q2 - q0q3) + bz * (q0q1 + q2q3));
wz = 2.0f * (bx * (q0q2 + q1q3) + bz * (0.5f - q1q1 - q2q2));
exMag = my * wz - mz * wy; // 三轴磁场和估计方向进行叉积运算,计算估计方向与三轴磁场的偏差
eyMag = mz * wx - mx * wz;
ezMag = mx * wy - my * wx;
// use un-extrapolated old values between magnetometer updates
// dubious as dT does not apply to the magnetometer calculation so
// time scaling is embedded in KpMag and KiMag
// 使用估计的旧值与磁力计值进行更新,dT不能应用在磁力计计算中,因此时间被嵌入在KpMag 和 KiMag里面
gx += exMag * eepromConfig.KpMag; // 比例增益控制磁强计收敛速度
gy += eyMag * eepromConfig.KpMag;
gz += ezMag * eepromConfig.KpMag;
if (eepromConfig.KiMag > 0.0f) // 用积分增益控制陀螺仪的偏差收敛速率
{
exMagInt += exMag * eepromConfig.KiMag;
eyMagInt += eyMag * eepromConfig.KiMag;
ezMagInt += ezMag * eepromConfig.KiMag;
gx += exMagInt;
gy += eyMagInt;
gz += ezMagInt;
}
}
//-------------------------------------------
// integrate quaternion rate
// 四元数微分方程,其中halfT为测量周期,g为陀螺仪角速度,其余都是已知量,这里使用了一阶龙格库塔法求解四元数微分方程。
q0i = (-q1 * gx - q2 * gy - q3 * gz) * halfT;
q1i = (q0 * gx + q2 * gz - q3 * gy) * halfT;
q2i = (q0 * gy - q1 * gz + q3 * gx) * halfT;
q3i = (q0 * gz + q1 * gy - q2 * gx) * halfT;
q0 += q0i;
q1 += q1i;
q2 += q2i;
q3 += q3i;
// normalise quaternion
// 四元数归一化,为什么又要归一化呢?这是因为引入了误差向量后四元数失去了规范性了(模不等于1了),所以要重新归一化
normR = 1.0f / sqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3);
q0 *= normR;
q1 *= normR;
q2 *= normR;
q3 *= normR;
// auxiliary variables to reduce number of repeated operations
// 把计算参考方向用到的值先都计算好,减少下面计算欧拉角时候的重复计算。
q0q0 = q0 * q0;
q0q1 = q0 * q1;
q0q2 = q0 * q2;
q0q3 = q0 * q3;
q1q1 = q1 * q1;
q1q2 = q1 * q2;
q1q3 = q1 * q3;
q2q2 = q2 * q2;
q2q3 = q2 * q3;
q3q3 = q3 * q3;
// 最后根据四元数方向余弦阵和欧拉角的转换关系,把四元数转换成欧拉角
sensors.margAttitude500Hz[ROLL] = atan2f(2.0f * (q0q1 + q2q3), q0q0 - q1q1 - q2q2 + q3q3);
sensors.margAttitude500Hz[PITCH] = -asinf(2.0f * (q1q3 - q0q2));
sensors.margAttitude500Hz[YAW] = atan2f(2.0f * (q1q2 + q0q3), q0q0 + q1q1 - q2q2 - q3q3);
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号