S型曲线规划

S型曲线规划

1 前言

S形加减速的最重要特征是该算法的加速度/减速度曲线的形状如字母 S。S形加减速的速度曲线平滑 ,从而能够减少对控制过程中的冲击，并使插补过程具有柔性 1
由于T形曲线在加速到匀速的切换过程中，实际中存在较大过冲，因此这里对比一下T曲线和7段S曲线的实际过程；

• T形：加速 -> 匀速 -> 减速
• S形：加加速(T1) -> 匀加速(T2) -> 减加速(T3)-> 匀速(T4)-> 加减速(T5)-> 匀减速(T6)-> 减减速(T7)

上文在加速这块的文字描述可能读起来起来有点绕，下面看图：

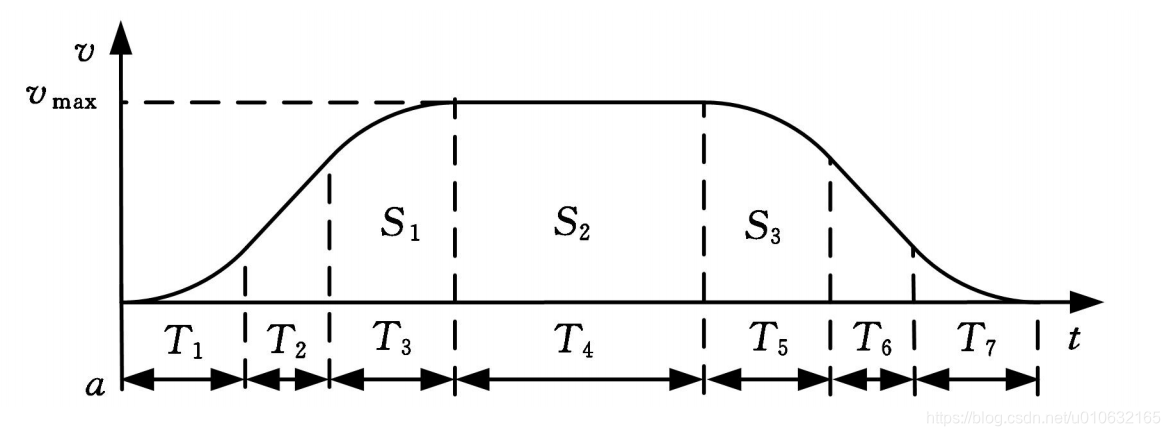
2 理论分析

由于S曲线在加减速的过程中，其加速度是变化的，因此这里引入了新的一个变量 J，即加加速度。

\[J = \frac{d_a}{d_t} \]

因此对应上图的7段S速度曲线中，规定最大加速为$$a_{max}$$，最小加速度为$$-a_{max}$$，则加速度的关系；

• 加加速(\(T_1\)) : a逐渐增大 , \(a=JT_1\) , \(0<t \leqslant t_1\)
• 匀加速(\(T_2\)) : a达到最大 , \(a=a_{max}\) , \(t_1<t\leq t_2\)
• 减加速(\(T_3\)) : a逐渐减小 , \(a=a_{max}-JT_3\) , \(t_2<t\leq t_3\)
• 匀速(\(T_4\)) : a不变化 , 此时 $$a=0$$ , \(t_3<t\leq t_4\)
• 加减速(\(T_5\)) : \(|a|\)逐渐增大 , 此时\(a=-JT_5\) , \(t_4<t\leq t_5\)
• 匀减速(\(T_6\)) : \(|a|\)逐渐增大 , 此时\(a=-a_{max}\) , \(t_5<t\leq t_6\)
• 减减速(\(T_7\)) : \(|a|\)逐渐增大 , 此时\(a=a_{max}+JT_7\) , \(t_6<t\leq t_7\)