基于云台结构的姿态旋转传递 - 基于四元数

基于云台结构的姿态旋转传递 - 基于四元数

通过基座姿态和云台关节角得到负载的姿态

参考文献：

四元数乘法：https://blog.csdn.net/benchuspx/article/details/108523498

四元数实现绕轴旋转：https://blog.csdn.net/cww_sh26/article/details/123339793

内旋和外旋:

https://www.cnblogs.com/Sandals-little/p/17641262.html

Math Basic

四元数乘法

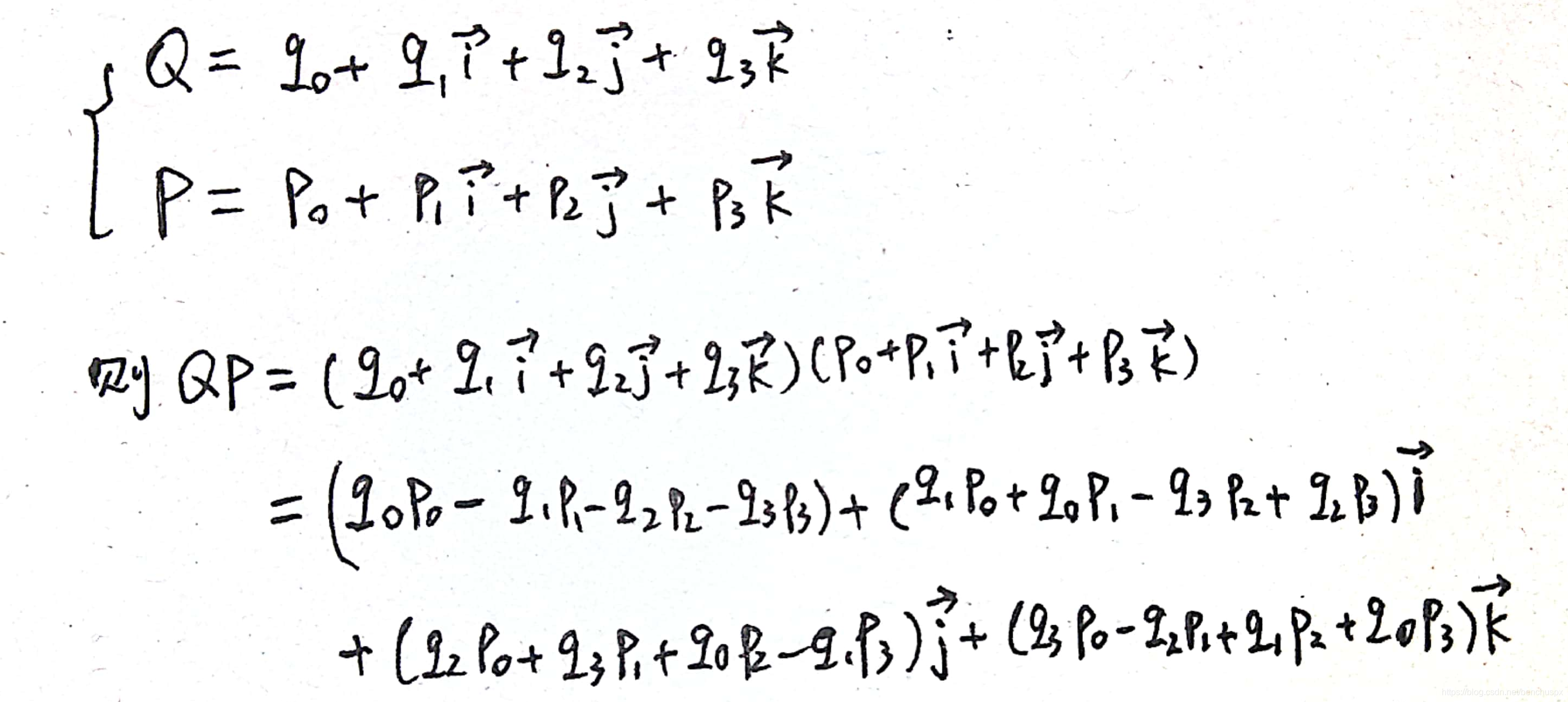
以机体坐标系做旋转

一个在机体坐标系下的旋转信息四元数 qB

只需要将 qB * (需要旋转的姿态qA) 即可得到以机体坐标系旋转后的qA，且qA的坐标系不改变

四元数绕轴旋转

问题：已知单位方向向量v=(vx,vy,vz),求绕v旋转角度ω(逆时针为正)的旋转矩阵。

实现方法：

首先计算单位四元素：q = (q0, q1, q2, q3)

• q0 = cos(ω/2)
• q1 = vx*sin(ω/2)
• q2 = vy*sin(ω/2)
• q3 = vz*sin(ω/2)

接着，使用单位四元素计算旋转矩阵;

void UnitQuaternion2Rotation(const double* q, double* rot) {
    rot[0] = q[0] * q[0] + q[1] * q[1] - q[2] * q[2] - q[3] * q[3];
    rot[1] = (q[1] * q[2] - q[0] * q[3]) * 2;
    rot[2] = (q[1] * q[3] + q[0] * q[2]) * 2;

    rot[3] = (q[2] * q[1] + q[0] * q[3]) * 2;
    rot[4] = q[0] * q[0] - q[1] * q[1] + q[2] * q[2] - q[3] * q[3];
    rot[5] = (q[2] * q[3] - q[0] * q[1]) * 2;

    rot[6] = (q[3] * q[1] - q[0] * q[2]) * 2;
    rot[7] = (q[3] * q[2] + q[0] * q[1]) * 2;
    rot[8] = q[0] * q[0] - q[1] * q[1] - q[2] * q[2] + q[3] * q[3];
}

基座姿态到负载姿态的传递

定义三轴的旋转角度，rotAngX rotAngY rotAngZ。分别表示绕轴X,Y,Z旋转的角度（右手定则？）

注意:旋转的角度需要遵循右手定则,不然角度会相反

获得分别绕X,Y,Z轴的旋转四元数（机体坐标系）

rotQX = quaternion(cos(rotAngX/2),1*sin(rotAngX/2),0,0);
rotQY = quaternion(cos(rotAngY/2),0,1*sin(rotAngY/2),0);
rotQZ = quaternion(cos(rotAngZ/2),0,0,1*sin(rotAngZ/2));

按照顺序应用传递：

假设初始姿态为 qa(大地坐标系)

qa = rotQY * rotQX * rotQZ * qa; //错误的,这个是外旋,姿态传递应当为外旋

正确的公式如下:

qa = qa * rotQZ * rotQX * rotQY;

得到的 qa 即为按照 Z -> X -> Y 轴旋转后的姿态信息(坐标系不变)

化简

三个四元数相乘可以化简成一个四元数直接与qa相乘

rotQX * rotQZ 化简结果

令 x = rotAngX / 2 z = rotAngZ / 2

\[qT = rotQX * rotQZ = cos(x)cos(z) + sin(x)cos(z)i - sin(x)sin(z)j+cos(x)sin(z)k \]

rotQY * qT 化简结果

令 y = rotAngY / 2，并令 qT中的实数项，ijk的系数分别为 a,b,c,d

\[rotQY * qT = (cos(y)a-sin(y)c) + (cos(y)b+sin(y)d)i+(sin(y)a +cos(y)c)j+(-sin(y)b+cos(y))k \]

即:

可以通过获得三轴关节角度和基座姿态来获取负载的姿态

Matlab 代码

function finRot = rotTransfer(q0,q1,q2,q3,angX,angY,angZ)

% qa = quaternion(0.931698,0.002579,-0.005492,0.363183);
qa = quaternion(q0,q1,q2,q3);

% rotAngX = deg2rad(angX)/2;
% rotAngY = deg2rad(angY)/2;
% rotAngZ = deg2rad(angZ)/2;s

rotAngX = angX/2;
rotAngY = angY/2;
rotAngZ = angZ/2;

rotQX = quaternion(cos(rotAngX),1*sin(rotAngX),0,0);
rotQY = quaternion(cos(rotAngY),0,1*sin(rotAngY),0);
rotQZ = quaternion(cos(rotAngZ),0,0,1*sin(rotAngZ));

% finRot = rotQY * rotQX * rotQZ * qa;
finRot = qa * rotQZ * rotQX * rotQY;	%这个才是正确的
%finRot = qa * rotQZ * rotQY * rotQX;

finRot = finRot.normalize();

% [e1,e2,e3] = quat2angle(finRot,"ZYX");
% e1 = rad2deg(e1);
% e2 = rad2deg(e2);
% e3 = rad2deg(e3);

end