python机器学习--监督学习002(线性模型算法)
线性模型
线性模型是在实践中广泛使用的一种模型,其利用输入特征的线性函数进行预测
回归问题的线性模型
对于回归问题,线性模型一般预测公式如下:
y = w[0]*x[0] + w[0]*x[0] + w[1]*x[1] + ... + w[p]*x[p] + b
这里的x是单个数据点的特征,w和b是学习模型的参数,y是预测结果
对于这个公式,可以将公式预测看为特征的加权求和
对于单一特征的预测结果是一条直线,两个特征时是一个平面,而更多特征时会是一个超平面
有许多的线性回归模型,而这些模型的区别在于如何从训练数据中得到w和b
线性回归(普通最小二乘法)
线性回归,又叫做最小二乘法,是回归问题最简单的也是最经典的线性方法。线性回归寻找w和b是的对训练集的预测值和真实值的回归目标y之间的均方误差
最小,均方误差是预测值和真实值之差的平方和除样本数。该方法最大的优点是其没有参数,但其也无法控制模型的复杂度
from sklearn.datasets import load_boston # 导入数据集
from sklearn.linear_model import LinearRegression # 导入线性回归算法
from sklearn.model_selection import train_test_split # 导入样本分割
my_dataset = load_boston()
x = my_dataset.data
y = my_dataset.target
X_train, X_test, y_train, y_test = train_test_split(x, y, random_state=0)
lr = LinearRegression()
lr = lr.fit(X_train, y_train) # 训练模型
print(lr.coef_) # w被存储在coef_ 属性中
print(lr.intercept_) # b被存储在 intercept_ 属性中
print(lr.score(X_test, y_test)) # 模型得分
# scikit-learn 总是将从训练集中的得到的值保存在下划线结尾的属性中
当训练集和测试集的性能有较大的差异是过拟合的明显标志
所以,我们需要一个可以控制复杂的模型,而对于标准线性回归最常用的代替方法之一就是岭回归
岭回归
岭回归也是一种回归的线性模型,因此它的预测公式和普通最小二乘法一致,但是在岭回归中,对于
系数w的选择,不仅仅是在训练集上得到好的预测结果,还要拟合附加的约束
我们希望w尽可能小,这样每个特征的影响都会尽可能小,同时仍给出较好的预测结果,这种约束就是所谓的:
正则化的一个例子,正则化是指对模型做出显示约束,来避免过度拟合,使用了L2正则化,使每个w都接近0
岭回归算法位于
from sklearn.linear_model import Ridge
其使用方法和上面的线性回归一样
一般来说,岭回归的约束比线性回归更强,但其具有更强的泛化性,所以我们应该使用Ridge而非LinearRegression
Ridge模型在模型的简单性和训练集性能间做了权衡,简单性和训练集性能二者对模型的重要程度可以通过用户设置
alpha参数来设定,默认的参数为1,增大alpha会使系数更加趋近于0,从而降低训练集性能,但可能会提高泛化性
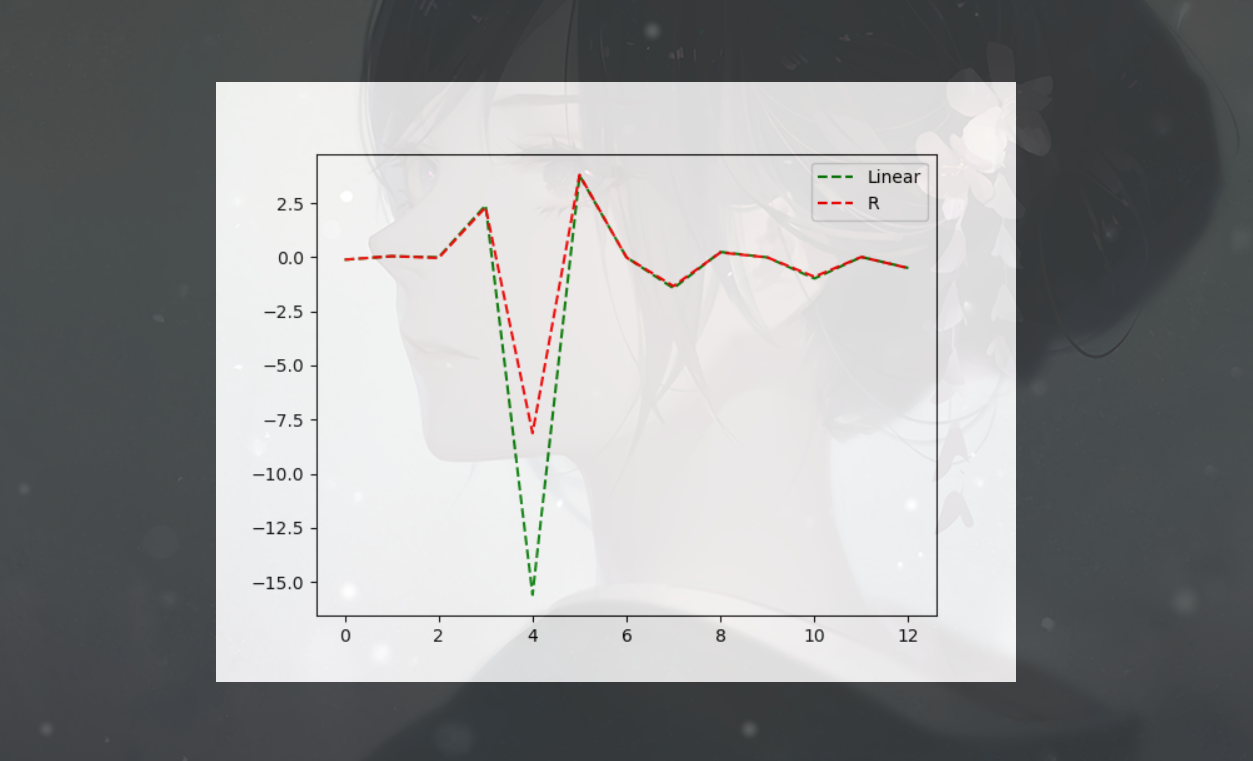
如果训练集较小,线性回归难以学到内容,而随着数据点越来越多,线性回归的效率逐渐的追上了岭回归w如下
该训练集比较巧合,大多数点都相同,只是巧合
lasso
也是一种正则化约束的线性模型,和岭回归相同,其也是约束系数接近于0,但是使用的方法不同。
叫做L1正则化,其结果是使某些系数刚好为0,说明某些特征的影响可以被模型完全忽略,这可以看为是一种
自动化的特征选择。
from sklearn.linear_model import Lasso
该模型的两个参数:
alpha: 限制
max_iter: 运行最大迭代次数
根据实际应用的测试,在Lasso回归和岭回归中,一般会优先采用岭回归,但是如果特征很多,而仅仅其中一些是比较重要的,
可以使用Lasso回归
分类问题的线性模型
二分类的情况下:
y = w[0]*x[0] + w[0]*x[0] + w[1]*x[1] + ... + w[p]*x[p] + b > 0
该公式和线性回归的公式非常相似,但是并没有返回特征的加权和,而是设置了阈值(0) 若函数小于0,就预测
类别-1,如果函数值大于0,就预测+1,对于所有的分类的线性模型,其规则都是通用的,不同的则是找出w和b的方法
对于用于回归的线性模型,输出y是特征的线性函数,是直线,平面或者超平面.对于用于分类的线性模型,决策边界是
输入的线性函数,也就是分类是利用直线,平面,或者超平面来分开两个类别的分类器。
最常见的两种线性分类算法是Logistic回归 和 线性支持向量机(线性SVM),对于这两种向量机都默认使用了L2正则化
对于Logistic回归和线性SVM,决定正则化强度的权衡参数叫做C。C越大,正则化越弱。及C越大,就越拟合
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np
cancer = load_breast_cancer()
X = cancer.data
y = cancer.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
log_mod = LogisticRegression().fit(X_train, y_train)
print('对于Log模型')
print('测试集分数:{}'.format(log_mod.score(X_test, y_test)))
print('训练集分数:{}'.format(log_mod.score(X_train, y_train)))
当测试集和训练集分数很接近时,可能出现了欠拟合现象,对于LogisticRegression模型可以考虑增大C值,降低
正则化程度。
许多线性分类模型仅仅适用于二分类问题,不能轻易的推广到多分类问题。所以针对于多分类问题,通常都使用一种叫做
‘一对其余’的方法。该方法将每个类别都学习一个二分类模型,生成多个二分类模型。在测试点上运行所有的二分类器来进行预测
在对应类别上获得的分数最多的分类器胜出。并将结果返回
多分类问题
每个类别都对应一个二分类分类器,这样每个类别都有一个系数w和一个截距b。其结果中最大值对应的类别即为预测类别
w[0]*x[0]+w[1]*x[1]+w[2]*x[2]+w[3]*x[3]+.。。+b
而Logistic回归背后的数学与一对多余的算法有些不同。但是也是用相同的预测方法
from sklearn.svm import LinearSVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np
iris_data = load_iris()
X = iris_data.data
y = iris_data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
l_svm = LinearSVC(max_iter=10000)
l_svm.fit(X_train, y_train)
print(iris_data.feature_names)
print(l_svm.coef_)
print(l_svm.score(X_test, y_test))
结果:
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
[[ 0.18424266 0.45123828 -0.8079416 -0.45071461]
[ 0.10194755 -0.93131594 0.31126594 -0.78899307]
[-0.74432787 -1.206418 1.36542537 1.58084703]]
1.0
成功率特别高。。。
线性模型优缺点
线性模型的主要参数是正则化参数,在回归模型中叫做alpha,在分类中叫做C
alpha较大或者C较小时,正则化的程度越大,w越靠近0,模型越简单
L1正则化: 一些特征被置0
L2正则化: w被接近于0,但不为0
优点:
线性模型的训练速度非常快,并且预处速度也非常快,可以推广到大的数据集,对稀疏数据也有效
线性模型的公式较简单的去理解
缺点:
线性模型往往并不清楚系数为什么是这样,并且当特征中有高度相关的
ps:
方法链---> 因为fit方法返回的都是self,所以被支持 object = LogisticRegression().fit(X,y)
这种方法调用的拼接被称为方法链


 浙公网安备 33010602011771号
浙公网安备 33010602011771号