python机器学习--监督学习001（K近邻算法）

K近邻算法

K-NN 算法可以说是最简单的机器学习算法，构建模型仅仅需要保存训练数据集即可，若要对新的数据点进行预测，算法会在
训练数据集中找到最近的数据点

K近邻分类

最简单的情况:仅考虑一个最近邻，在新数据点外寻找距离最近的数据点

---

除了仅仅有一个最近邻外，我们还可以考虑任意个邻居(k个)，这就是k近邻算法的由来，
在多于一个邻居的情况下，我们用投票法来指定标签，对于每个测试点，我们查询多少个
邻居属于1，多少邻居属于0，后选择次数更多的作为类别

步骤(以乳腺癌数据集为例):
    1.导入数据集
        from sklearn.datasets import load_breast_cancer
    2.导入数据分割函数
        from sklearn.model_selection import train_test_split
    3.导入K近邻算法
        from sklearn.neighbors import KNeighborsClassifier

    4.拿到数据集
        my_datasets = load_breast_cancer()

    5.拿到X(数据)和y(标签)
        X = my_datasets['data']
        y = my_datasets['target']

    6.按3:1分割训练集和测试集
        X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=0)

    7.实例化一个对象
        my_mol = KNeighborsClassifier(n_neighbors=3)

    8.对于K近邻算法，训练模型就是保存模型数据
        my_mol.fit(X_train,y_train)

    9.对模型进行评分
        my_mol.score(X_test,y_test)


    10.模型的使用
        my_mol.predict(X)


邻居个数和模型关系：
    由测试可以知道，当邻居个数越多，决策边界也会变得越平滑，更平滑的边界会有更简单的模型。
    所以，使用更少的邻居对应更高的模型复杂度，使用更多的邻居则会对应更低的模型复杂度

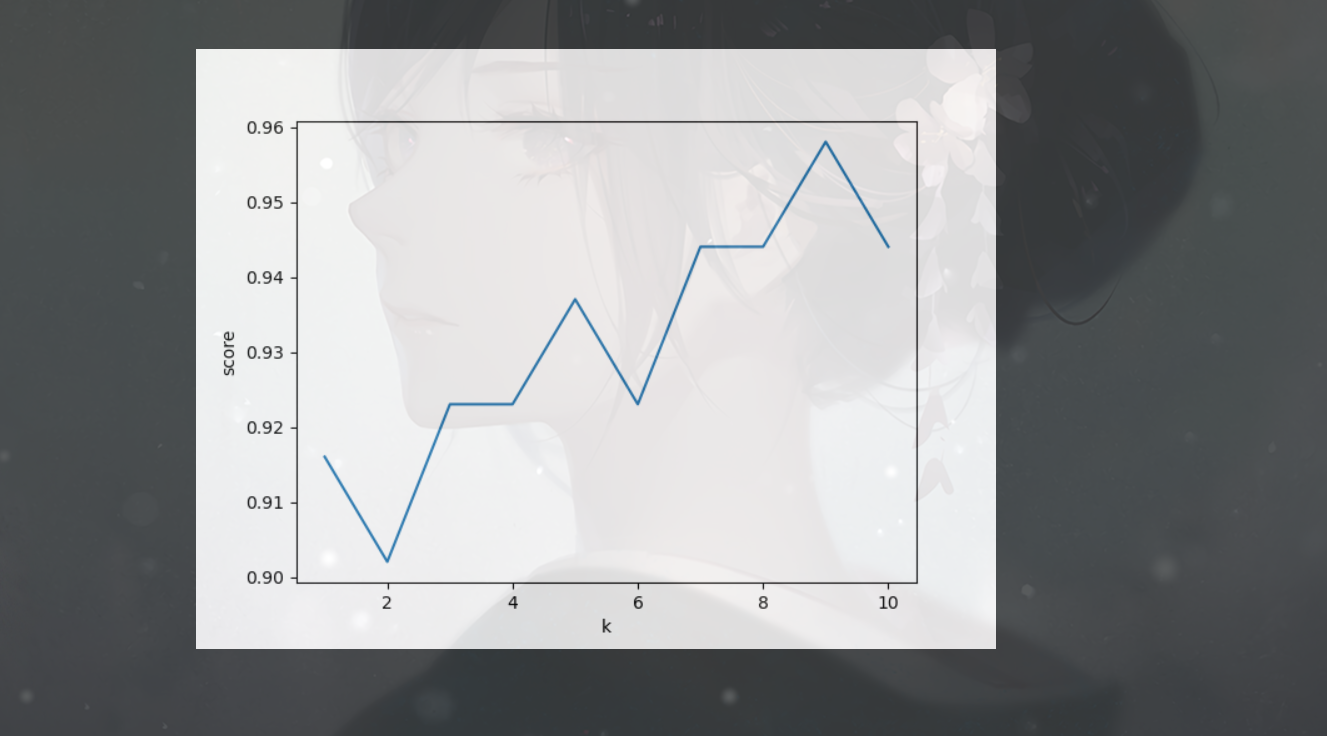
将邻居数1-10转换为可视图

---

score_list = []

for i in range(1, 11):
    clf = KNeighborsClassifier(n_neighbors=i)
    clf.fit(X_train, y_train)
    score_list.append(clf.score(X_test, y_test))

plt.plot(range(1, 11), score_list, label='test_score')
plt.xlabel('k')
plt.ylabel('score')
plt.show()

k近邻回归

k近邻算法还可以应用在回归问题上

在回归问题上，若使用单一近邻，那么预测结果就是最近邻目标值
若使用多近邻进行回归，则预测值为这些值的平均值

1.导入包
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor  # K近邻回归算法

2.拿数据集
my_datasets = load_boston()
X = my_datasets.data
y = my_datasets.target

3.分割数据
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

4.拿到算法对象
reg = KNeighborsRegressor(n_neighbors=3)

5.训练模型
reg.fit(X_train, y_train)

6.测试精度
print(reg.score(X_test, y_test))
该方法返回的是 R^2 R^2被称为决定系数，是回归模型预测的优度度量，位于0-1间，
越接近1，效果越好，当大于0.8时，认为较好


对于K近邻回归模型，仅有一个邻居时，训练集中的每个点都对预测结果有较大影响，导致预测结果非常不稳定
当考虑更多邻居时，预测结果会更加平滑，但是对于训练数据的拟合效果会降低

k近邻算法的优缺点和参数

一般来说，KNeighbors分类器有两个重要的参数:
    邻居个数，数据点间距离的度量方法
    在实践中，使用较小的邻居个数(3-5)往往可以得到较好的结果
    而数据点距离的度量方法默认使用欧式距离

优缺点：
    模型便于理解，不需要过多的调试
    构建模型的速度很快，但是若是训练集很大，则预测速度会较慢

    在使用KNN算法时，对数据的预处理很重要
    这一算法对特征非常多的数据集效果并不很好
    对于特征的大多数取值为0的数据集(所谓的稀疏数据集)效果非常不好

    由于本算法的局限性(预测速度和特征数)
    本算法在实践中其实使用较少