BA的简单实现

解bundle adjustment，由于完全是自己实现这份代码还是存在很大的缺陷，残差只能降低20倍（但是，它至少能下降，能收敛...）。目前看来，仅仅能作为对整个BA过程理解的代码，实际应用概率不大。

本来想实现DSO中的滑窗优化，可是写到后来发现这个东西还是需要前端来支持的，最起码得形成一个由窗口、相机参数、路标参数组成的流式数据结构才能进行完整地滑窗优化。所以目前退而求其次，解个BA就算了。由于完全是自己实现这份代码还是存在很大的缺陷，残差只能降低20倍（但是，它至少能下降，能收敛...）。接下来直接开始正文吧。

公式推导

关于BA的过程这里不展开，只说这份代码干了什么。在关于BA中梯度求法的总结中，附带总结了BA的过程。

Hession矩阵中各个小块的定义

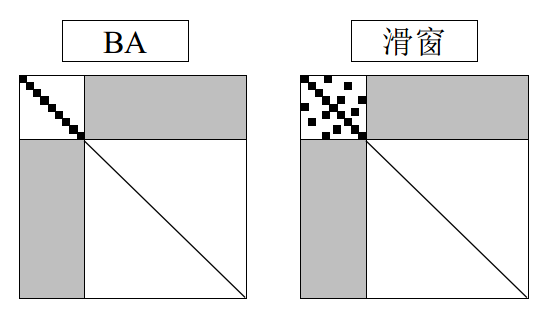
BA初始情况如上图左所示，这是在关于BA中梯度求法的总结中的\(J\)进行\(H=J^tJ\)的结果。根据\(J\)的格式，可以推导出，\(H\)共有四个部分，三种类型的矩阵块组成。

\[H=\left[ \begin{array}{cccc} \{B\}_{ii} & \{E\}_{ik} \\ \{E^T\}_{ki} & \{C\}_{kk} \end{array} \right] \]

其中\(i \in 1...m\)为相机的下标，\(k \in 1...n\)为路标点的下标。\(B\)为相机的部分，\(C\)为点的部分，\(E\)为联合的部分。显然左上角\(B\)共有\(m\times m\)个块，右上角\(E\)共有\(m\times n\)个块，右下角\(C\)共有\(n\times n\)个块。其中\(B,C\)都为对角块矩阵。

残差中的各偏导

上一小节已经将Hession的各个部分的大致分布说明。接下来要进行各个部分的推导，这需要进行残差的各个偏导的说明。
由于优化变量是相机位姿\(\xi\)和路标点\(P\)。所以\(J^TJ\delta x = -J^Tr\)这个公式解的\(\delta x\)是一个\((md_{cam} + nd_{point}) \times 1\)的向量。从上到下分别是各个相机的更新量和各个路标点的更新量，很容易验证这和Hession的维度的意义是统一的。
求Hession实际上就是求J，J是一个\(ld_{res} \times (md_{cam} + nd_{point})\)的矩阵，其中\(l\)为残差个数。在实现中显然不能把J直接在代码中写出来，BA的残差数量是非常大的，点的数量也很多，很明显会爆内存。那么在代码中实际上就是将每个残差的信息分布到各个点、相机中的数据结构中去。下面给出残差对于各个相机、路标点的梯度的定义。

\[{J_\xi}_{ik} = \frac{\partial r_{i}^k}{\partial \xi_i}, {J_P}_{ik} = \frac{\partial r_{i}^k}{\partial P_k} \]

这两个偏导的实际表达式在关于BA中梯度求法的总结中已经提到。\(r_{i}^k\)表示第\(i\)个相机看到了第\(k\)个路标点，如果没有看到，这一项为0。对应的导数项也为0。当然\(r_{i}^k\)只存在一项，即第\(i\)个相机不能两次看到第\(k\)个路标点，这样就无法确认该计算哪个，这在BAL的数据集中也是可以验证的。

\(\{B\}_{ii}\)

\[\{B\}_{ii} = \sum_{k=1}^{n}{J_\xi}_{ik}^T{J_\xi}_{ik} \]

\(\{E\}_{ik}\)

\[\{E\}_{ik} = {J_\xi}_{ik}^T{J_P}_{ik} \]

\(\{C\}_{kk}\)

\[\{C\}_{kk} = \sum_{i=1}^{m}{J_P}_{ik}^T{J_P}_{ik} \]

等式的右边

\(J^TJ\delta x = -J^Tr\)等式右边显然也和\(\delta x\)维度相同且同样分为两部分，上面是残差对于相机的倒数转置乘以残差，下面是路标点的倒数转置乘以残差。在BAL问题中残差是2维的，相机是9维的，点是3维的。

\[J^Tr =\left[ \begin{array}{cccc} J_{\xi}^Tr \\ J_{P}^Tr \end{array} \right] = \left[ \begin{array}{cccc} \{\sum_{k=1}^{n} {J_\xi}_{ik}^Tr_{i}^k\}_i \\ \{\sum_{i=1}^{m} {J_P}_{ik}^Tr_{i}^k\}_k \end{array} \right] \]

至此，具体的各矩阵块就清楚了。

舒尔补的引入

不加证明的引入舒尔补的操作过程：

\[\begin{array}{cccc} [B-EC^{-1}E^T] \delta x_{\xi} = -J_{\xi}^Tr + EC^{-1}J_{P}^Tr\\ \delta x_{P} = C^{-1}(-J_{P}^Tr - E^T\delta x_{\xi}) \end{array} \]

关键问题是如何去完成这个舒尔补的操作，总不能把\(E,J_{\xi}^Tr,J_{P}^Tr,EC^{-1}J_{P}^Tr\)拼出来再去算这个公式吧。\(E,J_{\xi},J_{P}\)可都是很大的矩阵，稍微上点规模的BA肯定是没办法这么算的。但是虽然这些元素都比较大，他们组成的东西在第一个第一个求相机更新量时的矩阵是比较小的。总的来说，对于第一个公式拼出下面这些量就解决了第一个公式的问题（第一个公式没有稀疏性，只能硬算，拼出来等式两边解方程组即可）

\[\begin{array}{cccc} EC^{-1}E^T\\ J_{\xi}^Tr\\ EC^{-1}J_{P}^Tr \end{array} \]

而这三个矩阵本身并不大，可以采用提前讲残差项、点、相机的信息分布开来，之后统一集中起来的策略。
对于第二个公式，其实相对来说更好解决一点，首先等式左边的\(C^{-1}\)是一个对角块矩阵，这个可以最后再考虑。\(-J_{P}r - E^T\delta x_{\xi}\)分别是两个向量，都可见下面分析。总的来说第二个公式要求这些量

\[\begin{array}{cccc} J_{P}^Tr \\ E^T\delta x_{\xi} \end{array} \]

\(EC^{-1}E^T\)

仔细观察\(B\)的结构可以知道最终的\(EC^{-1}E^T\)本身并不大只与相机位姿个数有关，而且\(E,C\)本身都是矩阵块，有\(m\times m\)个小块组成，记每个小块为\({\{EC^{-1}E^T\}}_{ij}\)，那么可以通过基本的矩阵乘法得到

\[{\{EC^{-1}E^T\}}_{ij} = \sum_{k=1}^{m}E_{ik}C_{kk}^{-1}E_{jk}^T \]

\(J_{\xi}^Tr\)

\(J_{\xi}^Tr\)是一个比较短的向量，\(r\)是一个\(d_{res} \times 1\)的向量，\(J_{\xi}\)是\(d_{res} \times (md_{cam}+nd_{point})\)的矩阵。一个残差项其实对于相机的梯度在整个大雅克比矩阵来讲就是在这个相机上位置上叠加一个雅克比。所以可以在计算残差时，分别求出残差对相机的梯度，然后把这个梯度直接加到相机上去。额好像在上面说了具体表达式了，查看残差中的各偏导-等式的右边这一节。

\[\{J_{\xi}^Tr\}_i = \sum_{k=1}^{n}{J_\xi}_{ik}^Tr_{i}^k \]

\(EC^{-1}J_{P}^Tr\)

\[\{EC^{-1}J_{P}^Tr\}_i = \sum_{k=1}^{m}E_{ik}C_{kk}^{-1}\{J_{P}^Tr\}_k \]

\(J_{P}^Tr\)

\[\{J_{P}^Tr\}_k=\sum_{i=1}^{m}{J_P}_{ik}^Tr_{i}^k \]

\(E^T\delta x_{\xi}\)

\[\{E^T\delta x_{\xi}\}_{k} = \sum_{i=1}^{m}E_{ik}^T {\delta x_{\xi}}_i \]

\(\delta x_p\)

\[\{\delta x_p\}_k = C_{kk}^{-1}(-\{J_{P}^Tr\}_k - \{E^T\delta x_{\xi}\}_{k}) \]

至此，公式最细节的部分已经描述完毕，接下来再说说代码中是如何安排这些中间变量的。

• 首先，系统会进入很多相机、点。接着必须传进来残差项，每个残差项和一个相机，一个点项关联，可以求出对相机的导数，对点的导数，这在代码中的ResidualBA::computeRes被计算，对相机的导数为jdrdcam，对点的导数为jdrdPw。
• 接着求出上面需要的\(\{J_{P}^Tr\}_k\)和\(\{J_{\xi}^Tr\}_i\)，分别为jPw_r,jcam_r两个变量。
• 当残差被插入系统时，要将残差包含的4个变量合理地组成上面公式中的小矩阵块，存入合适的位置。其中\(E_{ik}\)是存在Point的类内的变量名为Eik是一个数组，有m维，第i个元素表示该点和第i个相机的Eik。而C_{kk}和点完全绑定，存在点里，名字就叫C。当残差被加入系统时，首先调用ResidualBA::applyDataToPoint讲该被加到点上的数据加到点上。该加到相机上的数据加到相机上，具体参考代码。
• 当残差被插入系统时，对矩阵左上角的信息改动被实现在HessionStructBA::applyRes中，HessionStructBA中存的就是Hession矩阵的相机部分，applyRes就是算\(B\)的过程，可以参考代码很容易理解。
• 当要开始计算时，首先要算\([B-EC^{-1}E^T]\)，这在HessionStructBA::stepApplyPoint中被实现。

    void stepApplyPoint(Point_t *point, int camSize) override {
        //对每个点，统计信息到B
        //这个函数进行舒尔布的计算，主要是将点的信息更新到相机的hession块上
        for (int k = 0; k < camSize; ++k) {
            for (int l = 0; l < camSize; ++l) {
                if(point->ifHasEik(k) && point->ifHasEik(l))
                    addCamBlock(k,l,
                            -point->getEik(k)
                            * point->getC().inverse()
                            * point->getEik(l).transpose());
            }
        }
    }

• 舒尔补的信息好了，组织第一个公式的右边向量，这在WindowOptimizor::step_once中实现。

    for (int k = 0; k < camSize; ++k) {
        if(point->hasResidualWithTarget(k))
            cameras[k]->einvCJpR += point->getEik(k)
            *point->getC().inverse()*(-point->getJp_r());
    }
    Mat optRight = Eigen::Matrix<SCALAR,
        WINDOW_SIZE_MAX*FRAME_DIM,1>::Ones();
    for (int i = 0; i < camSize; ++i) {
        optRight.block(i*FRAME_DIM,0,FRAME_DIM,1) = -cameras[i]->jx_r-cameras[i]->einvCJpR;;
    }

• 接下来就是解第一个方程组了，在HessionStructBA::solveStep中实现。
• 解了第一个方程组，就可以更新相机的变量了，这个涉及到李代数在李群上的叠加后映射到李代数。具体参考代码，和上一篇文章的内容是一样的。
• 得到了相机的更新量，接下来计算点的更新量，在Point::getDelta中实现

    void getDelta(const Mat &camDelta){
        Eigen::Matrix<SCALAR,POINT_DIM,1> EikCamDelta;
        int camNum = camDelta.rows()/FRAME_DIM;
        for (int i = 0; i < camNum; ++i) {
            if(Eik[i]){
                EikCamDelta+=Eik[i]->transpose()*camDelta.block(i*FRAME_DIM,0,FRAME_DIM,1);
            }
        }
        delta = C.inverse()*(-jp_r-EikCamDelta);
    }

• 如果要更新点的更新量，直接加即可。

• 可以看到，我的代码还仅仅是最基础的高斯牛顿加了点调步长的代码。实际上还需要再实现LM算法，还会涉及到解约束最优化问题，还要考虑给每个维度加权重。想想都头大。