本质矩阵恢复相机位姿

本质矩阵可以在网上找到很多相关推导方式，可以很容易的推出其表达式为\(\boldsymbol{E}=[\boldsymbol{t}]_\times \boldsymbol{R}=\boldsymbol{SR}\)，那么如何根据这个本质矩阵推导出相机位姿？本文参考《计算机视觉中的多视图几何》，并且进行了仔细的推导，特此记录以备后用。

结论

若\(\boldsymbol{E}\)的SVD分解为\(\boldsymbol{E}=\boldsymbol{U}diag(1,1,0)\boldsymbol{V^T}\)，记

\[\boldsymbol{W}=\left[ \begin{array}{cccc} 0&-1&0\\ 1&0&0\\ 0&0&1 \end{array} \right], \boldsymbol{Z}=\left[ \begin{array}{cccc} 0&1&0\\ -1&0&0\\ 0&0&0 \end{array} \right] \]

那么\(\boldsymbol{E}=\boldsymbol{SR}\)有如下两种可能的分解（忽略符号！）。

\[\boldsymbol{S}=\boldsymbol{U}\boldsymbol{Z}\boldsymbol{U}^T, \boldsymbol{R}=\boldsymbol{U}\boldsymbol{W}\boldsymbol{V}^T or \boldsymbol{U}\boldsymbol{W}^T\boldsymbol{V}^T \]

证明

证\(\boldsymbol{S}=\boldsymbol{U}\boldsymbol{Z}\boldsymbol{U}^T\)

这部分在书上一笔带过，\(\boldsymbol{S}\)的形式是根据它的左零矢量也是\(\boldsymbol{E}\)的左零矢量这样的实时来确定的。这句话其实有下面几个意思：

• \(\boldsymbol{E}\)和\(\boldsymbol{S}\)的左零空间相等，即存在向量\(\boldsymbol{x}\)，\(\boldsymbol{x^TE}=\boldsymbol{0} \Leftrightarrow \boldsymbol{x^TS}=\boldsymbol{0}\)。
  • 这个其实是比较容易理解的。\(\boldsymbol{R}\)是一个正交阵，\(\boldsymbol{E}\)和\(\boldsymbol{S}\)就差了一个\(\boldsymbol{R}\)，正交阵只改变向量的方向，不改变向量的大小。这样的话，\(\boldsymbol{x^TS}=\boldsymbol{0}\)，那么\(\boldsymbol{x^TE}=\boldsymbol{x^TSR}=\boldsymbol{0}\)，反过来更容易推出。
• \(\boldsymbol{S}\)的表达式可以根据\(\boldsymbol{E}\)和\(\boldsymbol{S}\)的左零空间相等这个前提推得，那么接下来就要推它了。

根据《计算机视觉中的多视图几何》结论A3.1，一般反对称矩阵（那个\([\boldsymbol{t}]_\times]\)，或者说\(\boldsymbol{S}\)），可以写为

\[\boldsymbol{S} = k\boldsymbol{U}\boldsymbol{Z}\boldsymbol{U}^T \]

记这个\(\boldsymbol{U}\)为\(\boldsymbol{U_1}\)即\(\boldsymbol{S} = k\boldsymbol{U_1}\boldsymbol{Z}\boldsymbol{U_1}^T\)，另一方面由题干\(\boldsymbol{E}=\boldsymbol{U}diag(1,1,0)\boldsymbol{V^T}\)，记这个\(\boldsymbol{U}\)为\(\boldsymbol{U_2}\)，即\(\boldsymbol{E}=\boldsymbol{U_2}diag(1,1,0)\boldsymbol{V^T}\)。
证\(\boldsymbol{U_1}==\boldsymbol{U_2}\)：
由\(\boldsymbol{E}\)和\(\boldsymbol{S}\)的左零空间相等，把\(\boldsymbol{U_1}\)和\(\boldsymbol{U_1}\)分别带进\(\boldsymbol{S}\)和\(\boldsymbol{E}\)。
那么存在\(\boldsymbol{x}\)，使得

\[\boldsymbol{x^T}k\boldsymbol{U_1}\boldsymbol{Z}\boldsymbol{U_1}^T=\boldsymbol{0} \Leftrightarrow \boldsymbol{x^T}\boldsymbol{U_2}diag(1,1,0)\boldsymbol{V}^T=\boldsymbol{0} \]

等式左边右乘一系列正交阵可以做如下变换：

\[\boldsymbol{x^T}\boldsymbol{U_1}\boldsymbol{Z}\boldsymbol{U_1}^T=\boldsymbol{0} \Leftrightarrow \boldsymbol{x^T}\boldsymbol{U_1}diag(1,1,0)=\boldsymbol{0} \]

等式右边右乘一系列正交阵可以做如下变换：

\[\boldsymbol{x^T}\boldsymbol{U_2}diag(1,1,0)\boldsymbol{V}^T=\boldsymbol{0} \Leftrightarrow \boldsymbol{x^T}\boldsymbol{U_2}diag(1,1,0)=\boldsymbol{0} \]

由于上面留个式子等价，所以到这里可以很容易看出来\(\boldsymbol{U_1}==\boldsymbol{U_2}\)，证的话就是把\(\boldsymbol{U_1}\)，\(\boldsymbol{U_2}\)和\(\boldsymbol{x}\)都拆成列，然后去实际地一乘，去分析它们的关系。由于等式中第三行被乘0忽略，所以只能确定\(\boldsymbol{U_1}\)，\(\boldsymbol{U_2}\)的前两行相等。但是\(\boldsymbol{U_1}\)，\(\boldsymbol{U_2}\)都是正交阵，所以第三行在前两行确定相等的情况下，必然也是相等的。
由此得证\(\boldsymbol{S}=\boldsymbol{U}\boldsymbol{Z}\boldsymbol{U}^T\)就是SVD分解\(\boldsymbol{E}\)得到的\(\boldsymbol{U}\)。

证\(\boldsymbol{R}=\boldsymbol{U}\boldsymbol{W}\boldsymbol{V}^T or \boldsymbol{U}\boldsymbol{W}^T\boldsymbol{V}^T\)

其实第二部分是比较好证的，也很简单，在此就直接贴出原文证明吧。

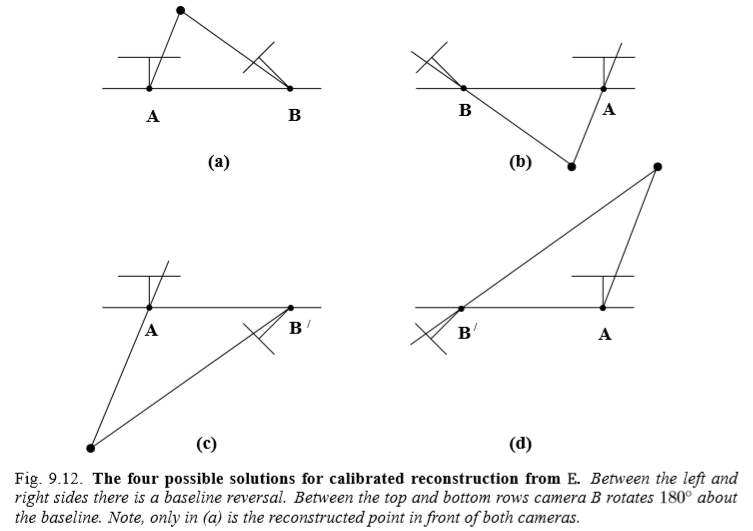
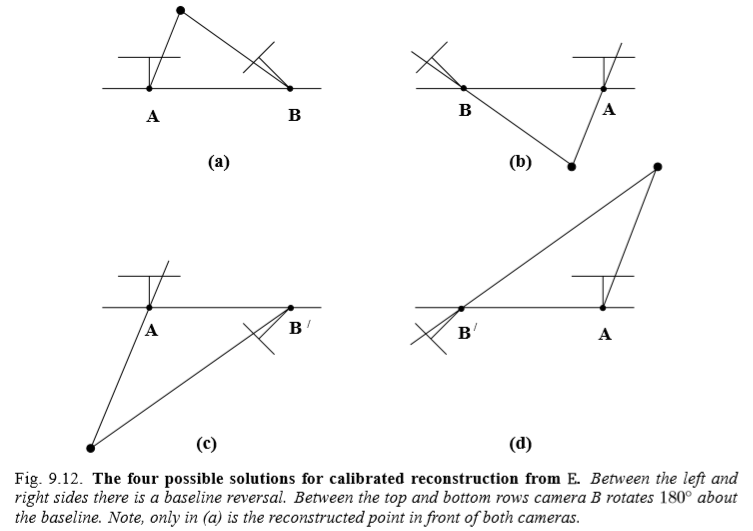
实际应用

注意到上面的证明中\(\boldsymbol{S}\)的符号是未知的，\(\boldsymbol{R}\)也有两种可能，这样总共就有四种可能。实际上只有一种情况能够将特征点都投影到两个相机的像平面前面，这样就只需要把四种情况带进去测试一下就可以了。

总结起来，要根据\(\boldsymbol{E}=\boldsymbol{SR}\)恢复出\(\boldsymbol{S}\)和\(\boldsymbol{R}\)，要进行如下步骤：

• 首先进行SVD分解得到\(\boldsymbol{E}=\boldsymbol{U}diag(1,1,0)\boldsymbol{V^T}\)

• 构成四种可能的情况，其中\(\boldsymbol{u}_3\)是\(\boldsymbol{U}\)的第三列（最后一列）：

  • \(\boldsymbol{T}_1 = [\boldsymbol{U}\boldsymbol{W}\boldsymbol{V}^T | \boldsymbol{u}_3]\)
  • \(\boldsymbol{T}_2 = [\boldsymbol{U}\boldsymbol{W}\boldsymbol{V}^T | -\boldsymbol{u}_3]\)
  • \(\boldsymbol{T}_3 = [\boldsymbol{U}\boldsymbol{W}^T\boldsymbol{V}^T | \boldsymbol{u}_3]\)
  • \(\boldsymbol{T}_4 = [\boldsymbol{U}\boldsymbol{W}^T\boldsymbol{V}^T | -\boldsymbol{u}_3]\)

• 将\(\boldsymbol{T}_1,\boldsymbol{T}_2,\boldsymbol{T}_3,\boldsymbol{T}_4\)和两相机都看到的一个世界坐标系特征点进行坐标系变换，找到能使该特征点在两相机坐标系下都在相机平面的正面\(\boldsymbol{T}_i\)即为最终解。