OI 中的一些零碎知识点

目录

\(\mathtt{0}\) 前言

本来想叫“OI 中的一些杂技”，但考虑到一些东西可能很实用，遂改成了现在的标题。

因为学的知识点有点杂，所以这篇博文啥都会讲点，可能会有一些 trick 和有趣的题。

写个自己看的，不保证能看懂。

\(\mathtt{1}\) Tarjan 及其相关

\(\mathtt{1/1}\) 桥

对于一张无向图 \(G\)，对于其中某条边 \(e\)，如果 \(G-e\) 的联通块数量增多，那么 \(e\) 就是 \(G\) 的一个桥。

考虑对 \(G\) 进行 DFS，我们会得到 树边 和 返祖边 两种类型的边，其中树边为位于 DFS 树上的边，返祖边为通过这条边能够返回到祖先的边。

考虑没有返祖边的情况，此时 \(G\) 是一棵树，割掉其中任意一条边都会导致图不连通，所以 \(G\) 里面的所有边都是桥。

如果有返祖边，我们割掉一条边后仍然可能通过返祖边返回，所以不能套用之前的方法。

处理这个问题的方法是 Tarjan 的核心：\(\mathrm{dfn}-\mathrm{low}\)

我们考虑维护每个点的 DFS 序 \(\mathrm{dfn}_i\)，那么两个点的 DFS 序关系就代表它们被访问的先后顺序，于是 DFS 树上祖先的 \(\mathrm{dfn}\) 一定小于子节点的 \(\mathrm{dfn}\)

那么我们就可以进一步对每个节点 \(x\) 维护“不经过父边，它能到的最小的 \(\mathrm{dfn}\) 值” \(\mathrm{low}_x\)，考虑维护它。对于它连接的所有非父边的边，我们分类讨论：如果该边为树边（对应点 \(i\) 还没被遍历），我们遍历它，同时将当前点的 \(\mathrm{low}_x\) 用 \(\mathrm{low}_i\) 更新；如果该边为返祖边（对应点 \(i\) 已被遍历），我们直接将 \(\mathrm{low}_x\) 用 \(\mathrm{dfn}_i\) 更新。

遍历完后，如果当前点 \(x\) 满足 \(\mathrm{dfn}_x=\mathrm{low}_x\)，则说明它能到的 DFS 序最小的点就是它本身，于是它的父边即为桥。

注意重边，请维护父边的编号而不是父亲来防止经过父边。

code

\(\mathtt{1/2}\) 割点

对于一张无向图 \(G\)，对于其中某个点 \(v\)，如果 \(G-v\) 的联通块数量增多，那么 \(v\) 就是 \(G\) 的一个割点。

思路和求桥是一样的，如果当前节点不经过父节点不能到更浅的地方（注意这里的判断条件是 \(\mathrm{low}_x\ge\mathrm{dfn}_f\)，因为即使到达父节点，父节点删掉后 \(x\) 依然到不了更浅的点），那么父节点就是割点。

但是有个特例：根节点显然不能到更浅的节点，所以只能暴力判删掉这个点后图的联通块数量是否增多。

code

\(\mathtt{1/3}\) 强连通分量

我们称有向图 \(G\) 强连通，当且仅当 \(G\) 中任意两个节点均联通。

强连通分量（SCC）为极大强连通子图。

有向图和无向图在 DFS 过程中最大的区别是有向图中多了一种“横跨边”，搬一张 oi-wiki 的图：

其中黑色边是树边，红色边是返祖边，蓝色边是横跨边，而绿色边是前向边。

流程类似，我们用一个栈来维护当前需要处理的点，显然强连通分量在 DFS 树上会有一个根节点，而整个分量就在其子树中，所以我们维护出 \(\mathrm{dfn}-\mathrm{low}\)，如果当前点 \(x\) 有 \(\mathrm{dfn}_x=\mathrm{low}_x\)，说明当前点无法到更浅的点，也就说明子树内所有还未处理的点都属于以 \(x\) 为根的强连通分量，由于我们使用栈进行维护，直接弹栈直到把 \(x\) 弹出去为止。

还有一种求 SCC 的算法叫 Kosaraju 算法，有时间了来补上。

code

\(\mathtt{2}\) 可并堆

以下的堆默认为小根堆。

\(\mathtt{2/1}\) 左偏树

不会，咕咕咕。

\(\mathtt{2/2}\) 配对堆

配对堆是一个满足堆性质的多叉树。一般使用儿子-兄弟表示法存储一棵配对堆，如图便是一棵配对堆：

struct E {
  int v, c, r; // 值；儿子；兄弟
} e[kN];

\(\mathtt{2/2/1}\) 合并

假设我们要合并堆 \(x,y\)，令 \(v_x<v_y\)，我们将 \(y\) 插入到 \(x\) 的儿子中即可。

int M(int x, int y) {
  if (!x || !y) {
    return x | y;
  }
  if (e[x].v > e[y].v) {
    swap(x, y);
  }
  e[y].r = e[x].c, e[x].c = y;
  return x;
}

\(\mathtt{2/2/2}\) 删除最小值

将问题转化为合并根的所有儿子。

考虑先将儿子两两配对进行合并，然后从右到左依次合并成最终的堆。

均摊复杂度 \(O(\log n)\)。

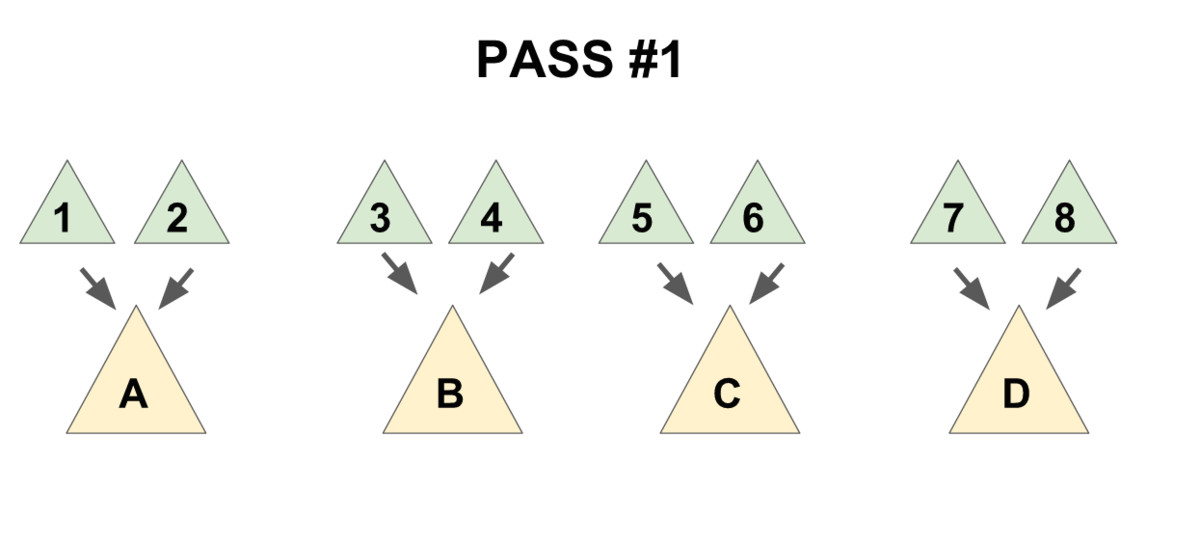
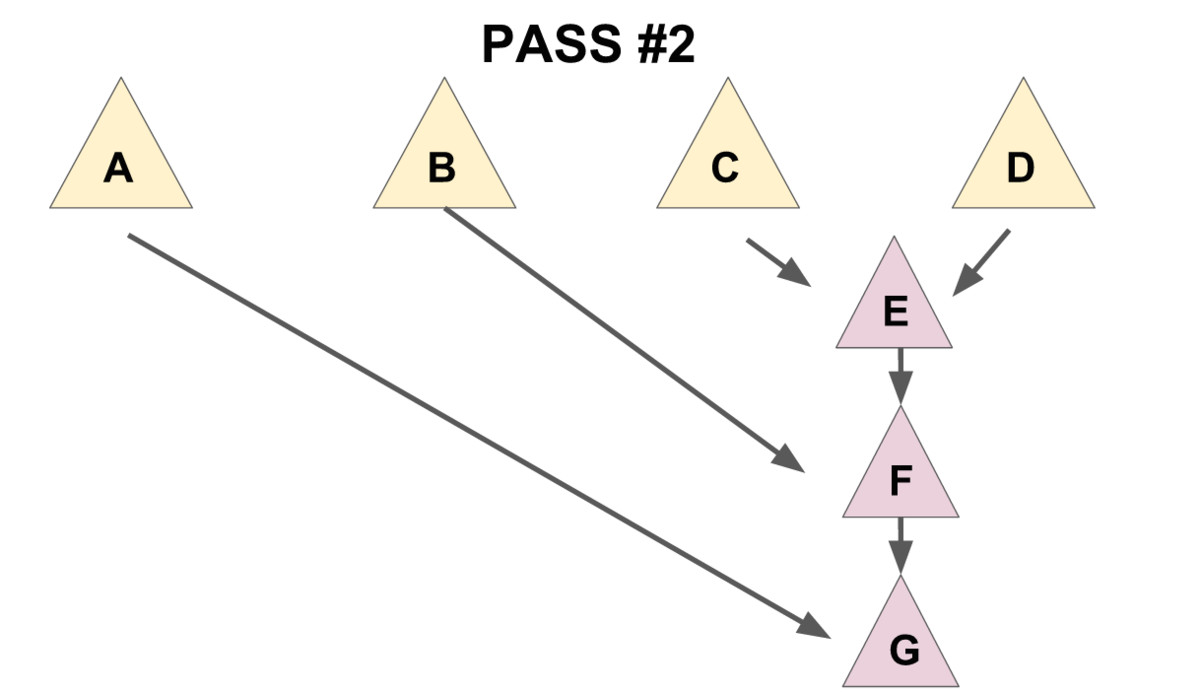
int C(int x) {
  if (!x || !e[x].r) {
    return x;
  }
  int y = e[x].r, z = e[y].r;
  e[x].r = e[y].r = 0;
  return M(C(z), M(x, y));
}

没了。

code

\(\mathtt{2/3}\) 斜堆

满足堆性质的二叉堆。

合并两个堆 \(x,y\) 时，我们令 \(v_x<v_y\)，将 \(x\) 的右子树和 \(y\) 递归合并，最后交换 \(x\) 的左右子树。

删除最小值直接合并根的左右子树即可。

逆天东西，我也不知道为什么复杂度是对的。

code

posted @ 2023-07-14 07:40  bykem  阅读(80)  评论(0)    收藏  举报