P8477 「GLR-R3」春分 题解

更好的阅读体验

牛逼逼题。

Subtask 1

直接暴力，每个实验配一块板。

需要 \(n^2\) 块板。

cout << n * n << '\n';
for (int i = 1; i <= n; ++i) {
  for (int j = 1; j <= n; ++j) {
    cout << "1 " << i << ' ' << ++c << ' ' << j << '\n';
  }
}

Subtask 2

注意到我们可以给每一种溶液配一块专属板，实验时挑出两种溶液配的板拼在一起即可。

需要 \(2n\) 块板。

cout << 2 * n << '\n';
for (int i = 1; i <= n; ++i) {
  for (int j = 1; j <= n; ++j) {
    cout << "2 " << i << ' ' << i << ' ' << n + j << ' ' << j << '\n';
  }
}

Subtask 3

考虑分组，我们把右边的溶液平均分为两组，记作 \(R_0\) 和 \(R_1\)，左边的溶液记作 \(L\)

那么我们考虑给 \(L\) 中每组溶液配一块专属板，这里需要 \(n\) 块板，然后给 \(R_0\) 中每组溶液配一块板，完成 \(L\times R_0\) 中的实验。

这时情况是这样的：

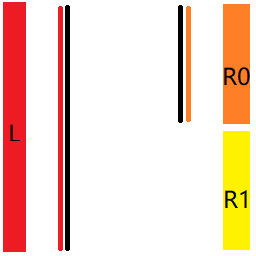
sub3-1

我们考虑复用 \(R_0\) 中的板，翻转后给 \(R_1\) 完成 \(L\times R_1\) 中的实验即可。

这时需要用 \(\lceil\frac{n}{2}\rceil+n\) 块板，会被卡。

发现 \(R_0\) 中多出来的那块板其实根本不需要，因为污染的地方只是内侧。而在处理 \(L\times R_1\) 里的实验时我们不需要内侧。

于是就只要 \(\lfloor\frac{n}{2}\rfloor+n\) 块板了。

\(\lceil\frac{n}{2}\rceil+n\)：

cout << (n + 1) / 2 + n << '\n';
for (int i = 1; i <= n; ++i) {
  for (int j = 1; j <= (n + 1) / 2; ++j) {
    cout << "2 " << i << ' ' << i << ' ' << n + j << ' ' << j << '\n';
  }
}
for (int i = 1; i <= n; ++i) {
  for (int j = (n + 1) / 2 + 1; j <= n; ++j) {
    cout << "2 " << i << ' ' << i << ' ' << -(n / 2 + j) << ' ' << j << '\n';
  }
}

\(\lfloor\frac{n}{2}\rfloor+n\)：

cout << n / 2 + n << '\n';
for (int i = 1; i <= n; ++i) {
  for (int j = 1; j <= n / 2; ++j) {
    cout << "2 " << i << ' ' << i << ' ' << n + j << ' ' << j << '\n';
  }
}
if (n & 1) {
  for (int i = 1; i <= n; ++i) {
    cout << "1 " << i << ' ' << i << ' ' << n / 2 + 1 << '\n';
  }
}
for (int i = 1; i <= n; ++i) {
  for (int j = (n + 1) / 2 + 1; j <= n; ++j) {
    cout << "2 " << i << ' ' << i << ' ' << -(n / 2 + j) << ' ' << j << '\n';
  }
}

Subtask 4

Subtask 3 最劣的地方在于 \(L\) 配板的右边本来都是干净的，结果被 \(R_0\) 配板污染了，这显然不是我们的意图。

考虑把 \(L,R\) 两边都均分成 \(3\) 组。给 \(L_0,L_1,L_2,R_0\) 各分配一块板。

那么第一步显然是把 \(L\times R_0\) 弄完。

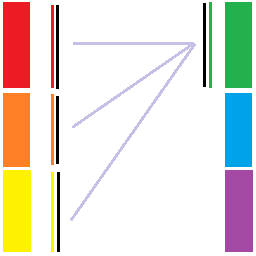
sub4-1

然后我们考虑将 \(L_2\) 的板拿给 \(R_1\) 用，然后将 \((L_0+L_1)\times R_1\) 弄完。

但这样会导致 \(L_0+L_1\) 的配板被污染了，很劣。

考虑 \(R_0\) 的配板，我们让它充当中间人，将干净的一面对着 \(L_0+L_1\)，脏的一面对着 \(R_1\)，于是 \(L_0+L_1\) 依然是干净的。

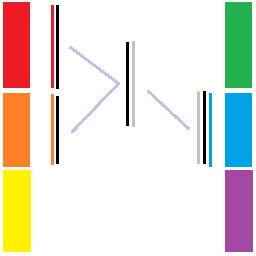
sub4-2

同样的，我们再把 \(L_1\) 的板给 \(R_2\) 用，然后用同样的方式处理 \(L_0\times R_2\)

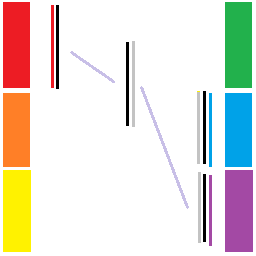
sub4-3

我们还剩下 \(L_2\times R_1+(L_1+L_2)\times R_2\) 没做，随便排列组合一下就行：

sub4-4

需要满足 \(s_{L_2}\ge s_{R_1},s_{L_1}\ge s_{R_2},s_{R_0}\ge s_{L_2},s_{L_0}\ge s_{L_1}\)，取：

\[s_{L_1}=s_{R_2}=\lfloor\frac{n}{3}\rfloor\\[5px] s_{L_2}=s_{R_1}=\lfloor\frac{n+1}{3}\rfloor\\[5px] s_{L_0}=s_{R_0}=\lceil\frac{n}{3}\rceil \]

即可。

sl1 = sr2 = n / 3;
sl2 = sr1 = (n + 1) / 3;
sl0 = sr0 = (n + 2) / 3;
for (int i = 1; i <= sl0; ++i) {
  l0[i] = ++c;
}
for (int i = 1; i <= sl1; ++i) {
  l1[i] = ++c;
}
for (int i = 1; i <= sl2; ++i) {
  l2[i] = ++c;
}
for (int i = 1; i <= sr0; ++i) {
  r0[i] = ++c;
}
cout << c << '\n';
for (int j = 1; j <= sr0; ++j) {
  for (int i = 1; i <= sl0; ++i) {
    cout << "2 " << i << ' ' << l0[i] << ' ' << r0[j] << ' ' << j << '\n';
  }
  for (int i = 1; i <= sl1; ++i) {
    cout << "2 " << sl0 + i << ' ' << l1[i] << ' ' << r0[j] << ' ' << j << '\n';
  }
  for (int i = 1; i <= sl2; ++i) {
    cout << "2 " << sl0 + sl1 + i << ' ' << l2[i] << ' ' << r0[j] << ' ' << j << '\n';
  }
}
for (int j = 1; j <= sr1; ++j) {
  for (int i = 1; i <= sl0; ++i) {
    cout << "3 " << i << ' ' << l0[i] << ' ' << r0[1] << ' ' << l2[j] << ' ' << sr0 + j << '\n';
  }
  for (int i = 1; i <= sl1; ++i) {
    cout << "3 " << sl0 + i << ' ' << l1[i] << ' ' << r0[1] << ' ' << l2[j] << ' ' << sr0 + j << '\n';
  }
}
for (int j = 1; j <= sr2; ++j) {
  for (int i = 1; i <= sl0; ++i) {
    cout << "3 " << i << ' ' << l0[i] << ' ' << r0[1] << ' ' << l1[j] << ' ' << sr0 + sr1 + j << '\n';
  }
}
for (int i = 1; i <= sl1; ++i) {
  for (int j = 1; j <= sr2; ++j) {
    cout << "2 " << sl0 + i << ' ' << -l0[i] << ' ' << l1[j] << ' ' << sr0 + sr1 + j << '\n';
  }
}
for (int i = 1; i <= sl2; ++i) {
  for (int j = 1; j <= sr1; ++j) {
    cout << "2 " << sl0 + sl1 + i << ' ' << r0[i] << ' ' << l2[j] << ' ' << sr0 + j << '\n';
  }
  for (int j = 1; j <= sr2; ++j) {
    cout << "2 " << sl0 + sl1 + i << ' ' << r0[i] << ' ' << l1[j] << ' ' << sr0 + sr1 + j << '\n';
  }
}

Subtask 5~7

观察 sub 4，我们发现其实只需要额外拿一块中间板就可以保持左右两边板的状态，于是我们可以空出来一个 \(R_0\) 来干一些奇奇怪怪的事情。

考虑将 \(L\) 分为 \(2\) 组，\(R\) 分为 \(3\) 组。给 \(L_0,R_0,R_1\) 各分配一块板。

首先第一步显然还是将 \(L_0\times(R_0+R_1)\) 的实验做了：

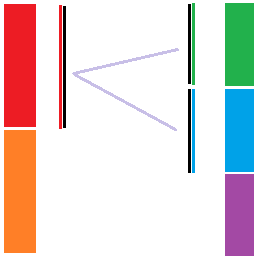
sub7-1

然后我们将 \(R_0\) 翻转后给 \(R_2\) 用，额外用一块中间板来隔绝 \(L_0\) 和 \(R_2\)，处理 \(L_0\times R_2\)：

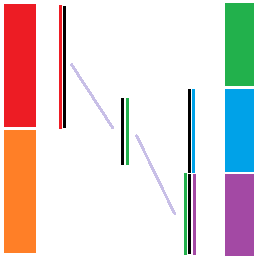
sub7-2

翻转 \(L_0\) 给 \(L_1\) 用，处理 \(L_1\times R_1\)：

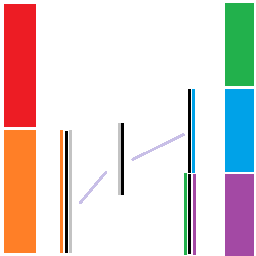
sub7-3

最后把 \(R_1\) 的板翻转后给 \(R_0\)，处理 \(L_1\times(R_0+R_2)\) 即可：

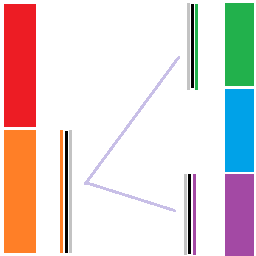
sub7-4

需要 \(s_{R_1}\ge s_{R_0}\ge s_{R_2},s_{L_0}\ge s_{L_1}\)，取

\[s_{L_0}=\lceil\frac{n}{2}\rceil,s_{L_1}=\lfloor\frac{n}{2}\rfloor\\[5px] s_{R_0}=\lfloor\frac{n+1}{3}\rfloor,s_{R_1}=\lceil\frac{n}{3}\rceil,s_{R_2}=\lfloor\frac{n}{3}\rfloor \]

即可。

代码实际上比 sub 4 还要好写一点。

for (int i = 1; i <= (sl = (n + 1) / 2); ++i) {
  l[i] = ++c;
}
for (int i = 1; i <= (sr0 = (n + 1) / 3); ++i) {
  r0[i] = ++c;
}
for (int i = 1; i <= (sr1 = (n + 2) / 3); ++i) {
  r1[i] = ++c;
}
sr2 = n / 3;
x = ++c;
cout << c << '\n';
for (int i = 1; i <= sl; ++i) {
  for (int j = 1; j <= sr0; ++j) {
    cout << "2 " << i << ' ' << l[i] << ' ' << r0[j] << ' ' << j << '\n';
  }
  for (int j = 1; j <= sr1; ++j) {
    cout << "2 " << i << ' ' << l[i] << ' ' << r1[j] << ' ' << sr0 + j << '\n';
  }
}
for (int i = 1; i <= sl; ++i) {
  for (int j = 1; j <= sr2; ++j) {
    cout << "3 " << i << ' ' << l[i] << ' ' << x << ' ' << -r0[j] << ' ' << sr0 + sr1 + j << '\n';
  }
}
for (int i = 1; i <= n / 2; ++i) {
  for (int j = 1; j <= sr1; ++j) {
    cout << "3 " << sl + i << ' ' << -l[i] << ' ' << -x << ' ' << r1[j] << ' ' << sr0 + j << '\n';
  }
}
for (int i = 1; i <= n / 2; ++i) {
  int d = sl + i;
  for (int j = 1; j <= sr0; ++j) {
    cout << "2 " << d << ' ' << -l[i] << ' ' << -r1[j] << ' ' << j << '\n';
  }
  for (int j = 1; j <= sr2; ++j) {
    cout << "2 " << d << ' ' << -l[i] << ' ' << -r0[j] << ' ' << sr0 + sr1 + j << '\n';
  }
}

record

code

posted @ 2023-06-23 18:23  bykem  阅读(40)  评论(0)    收藏  举报