SAM 学习笔记
字符串,太抽象!
前置知识
- 自动机
一些约定
若无特殊说明,以下默认字符串下标从 \(1\) 开始。
引入
在做字符串题的过程中,我们经常需要对一个字符串的所有子串做一些事情,但是直接暴力做是 \(\mathcal{O}(n^2)\) 的,非常慢。
于是有些毒瘤跳了出来,说:“我们能不能造出一个能够接受一个字符串 \(S\) 的所有子串的自动机,满足状态数和转移数都是 \(\mathcal{O}(n)\) 的呢?”
于是,SAM(Suffix Automaton)就这么诞生了。
基础想法
由于子串就是后缀的前缀,并且自动机天生就能接受一个串的所有前缀,那么我们就只需要能够接受所有的后缀就行了。
很不幸,直接暴力把后缀丢进 Trie 里复杂度是 \(\mathcal{O}(n^2)\) 的,我们需要优化。
可以发现对于一些状态,我们是可以合并的,具体的,对于两个状态,如果它们的入边和出边都是一样的,那么这两个状态就可以被合并。
但是按照这种规则进行合并构造 SAM,复杂度依旧是 \(\mathcal{O}(n^2)\) 的,没有改善。我们需要一些更强大的工具来帮助我们。
更进一步
进行合并后,一个状态能够接受的字符串将不止一个。例如,对于 \(s=\mathtt{aba}\),\(\mathtt{b}\) 和 \(\mathtt{ab}\) 将合并成一个状态(因为它们都由 \(\mathtt{b}\) 结束,且下一个能接的字符都是 \(\mathtt{a}\))。可以发现,这些字符串的长度是连续递增的,且前一个字符串是后一个字符串的后缀,这说明了我们实际上只要存储这个状态最长的字符串和最短的字符串,就可以完整的表示这个状态。
\(\text{endpos}\)、\(\text{endpos}\) 等价类与后缀链接
可以发现,对于两个子串,如果它们在 \(S\) 中的结束位置集合相同,那么它们会被合并到一个状态中(因为结束字符一样,且转移字符集也一样),这时,我们称这两个子串的 \(\text{endpos}\) 一样,被划分到同一个 \(\text{endpos}\) 等价类(即所有 \(\text{endpos}\) 相等的子串组成的集合)。
在最终的自动机中,对于一个状态 \(u\),我们记代表串是 \(u\) 的代表串的真后缀中的最长的那一个对应的状态为 \(v\),则 \(v\) 能接受的字符串都是 \(u\) 能接受的字符串的子串,我们称 \(v\) 是 \(u\) 的后缀链接,记作 \(v=\text{link}(u)\)。例如,对于 \(S=\mathtt{beef}\),最终的自动机里 \(\mathtt{bee,ee}\) 同时被一个状态接受,而 \(\mathtt{e}\) 是 \(\mathtt{ee}\) 的真后缀中最长的那一个,所以 \(\mathtt{e}\) 所属的状态就是 \(\mathtt{bee,ee}\) 所属的状态的后缀链接。
通过不断的走后缀链接,我们最终可以走出一个从空串开始的长度连续的字符串集合,所以,在接下来的 SAM 构造步骤的说明中,我们可以将后缀链接理解成对一个从空串开始的长度连续的字符串集合的划分。例如,对于 \(S=\mathtt{beef}\),最终的自动机里从 \(\mathtt{bee,ee}\) 开始不断跳后缀链接,最终得到的字符串集合为 \(\{\varnothing\mid\mathtt{e}\mid\mathtt{ee,bee}\}\)。由于在跳后缀链接的过程中,代表串长度不断递减,故不会出现循环。
如何构建 SAM
我们构建 SAM 的过程是在线的,即每次加入一个字符,动态维护 SAM 的结构。在一开始,我们只有一个空串。
对于当前要插入的字符 \(\mathtt{c}\),设上一次插入后的状态是 \(\text{last}\)(它的代表串为全串),则从 \(\text{last}\) 开始不断跳后缀链接,我们可以得到当前串的所有后缀,要再加入一个 \(\mathtt{c}\),只需将这些状态的转移中添加一个 \(\mathtt{c}\) 即可。最后,由于当前状态已经表示出了长度为 \([1,n]\) 的所有字符串,我们只需将它的后缀链接指向空串即可。
但是,我们可能在之前的插入中已经插入了一个 \(\mathtt{c}\)。假设我们在跳后缀链接的过程中碰到了一个状态 \(p\) 存在一个转移 \(\mathtt{c}\),设它转移到了状态 \(q\)。
这时,我们可以停止插入,因为我们只需把 \(q\) 中的只由 \(\mathtt{c}\) 转移过来的部分分裂出来,就可以接在当前状态的前面,所以只需把此状态分裂出来,把当前状态和 \(q\) 的后缀链接指向分裂出来的状态即可。
(注意,我们需要对所有由 \(\mathtt{c}\) 转移过来的部分分裂出来。因此,我们需要对 \(p\) 的后缀链接重复此过程。)
(其实就相当于把所有 \(\{\cdots\mid\mathtt{a,b,c,d}\mid\cdots\}\) 变成了 \(\{\cdots\mid\mathtt{a,b}\mid\mathtt{c,d}\mid\cdots\}\),然后更新受影响的状态,那么就可以把 \(\mathtt{a,b}\) 接在 \(\mathtt{c}\) 的前面,变成 \(\{\cdots\mid \mathtt{a,b}\mid \mathtt{c}\}\)。)
至此,我们就完成了 SAM 的构造。
P.S. 每次我在网上看到什么”复制“一份 \(q\) 到 \(\text{clone}\) 这种话都会很谔谔,因为啥都没复制,总信息量是不变的,只是把 \(q\) 进行了分裂,所以变量名叫 \(\text{split}\) 可能更贴切一点。
代码:
struct SAM {
struct E {
int n[26], ml, pr; // 转移,最大长度,后缀链接
} e[kN << 1];
int l, c;
SAM() { e[0].pr = -1; }
void I(char ch) {
ch -= 'a';
int x = ++c, p = l;
e[x].ml = e[l].ml + 1;
for (; ~p && !e[p].n[ch]; e[p].n[ch] = x, p = e[p].pr) { // 对当前字符串的所有后缀添加一个 ch
}
if (~p) { // 如果已经存在转移
int q = e[p].n[ch];
if (e[q].ml == e[p].ml + 1) { // 如果刚好就是自己想要的,此时不用分裂
e[x].pr = q;
} else {
int _q = ++c; // 分裂
copy(e[q].n, e[q].n + 26, e[_q].n);
e[_q].pr = e[q].pr, e[q].pr = _q, e[_q].ml = e[p].ml + 1;
for (; ~p && e[p].n[ch] == q; e[p].n[ch] = _q, p = e[p].pr) { // 更新 p 的后缀链接的转移
}
e[x].pr = _q; // 将 x 的后缀链接连到分裂出来的 q
}
}
l = x;
}
};
以下是菜鸡画的几张 SAM 构造流程图:
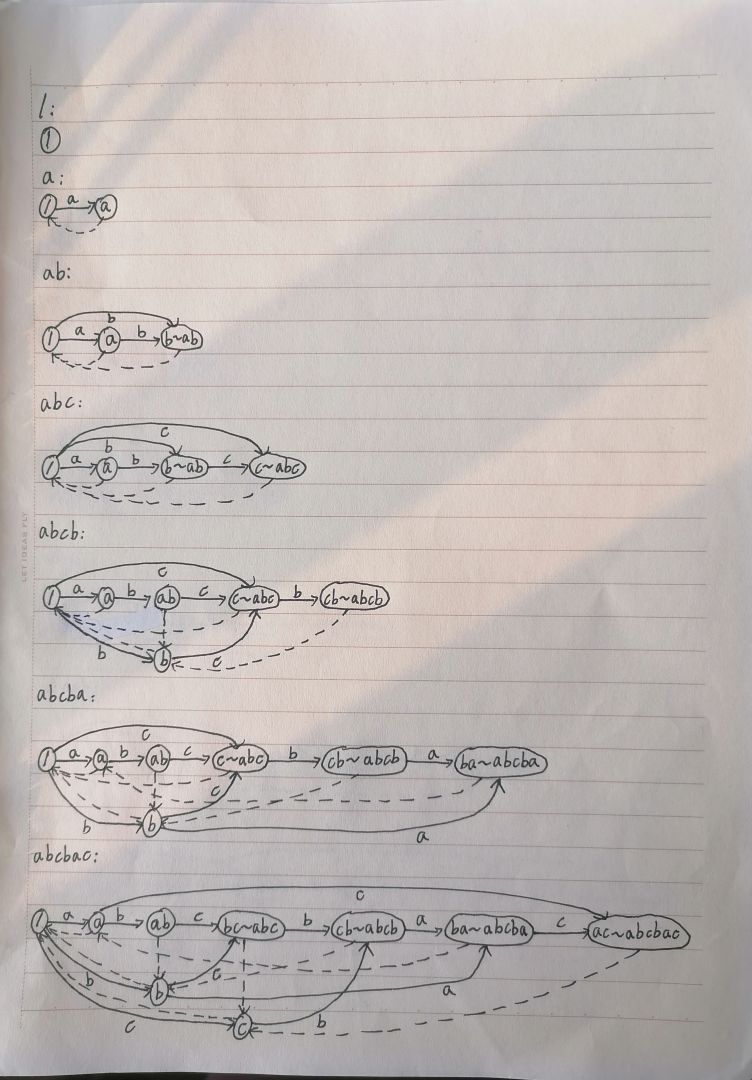
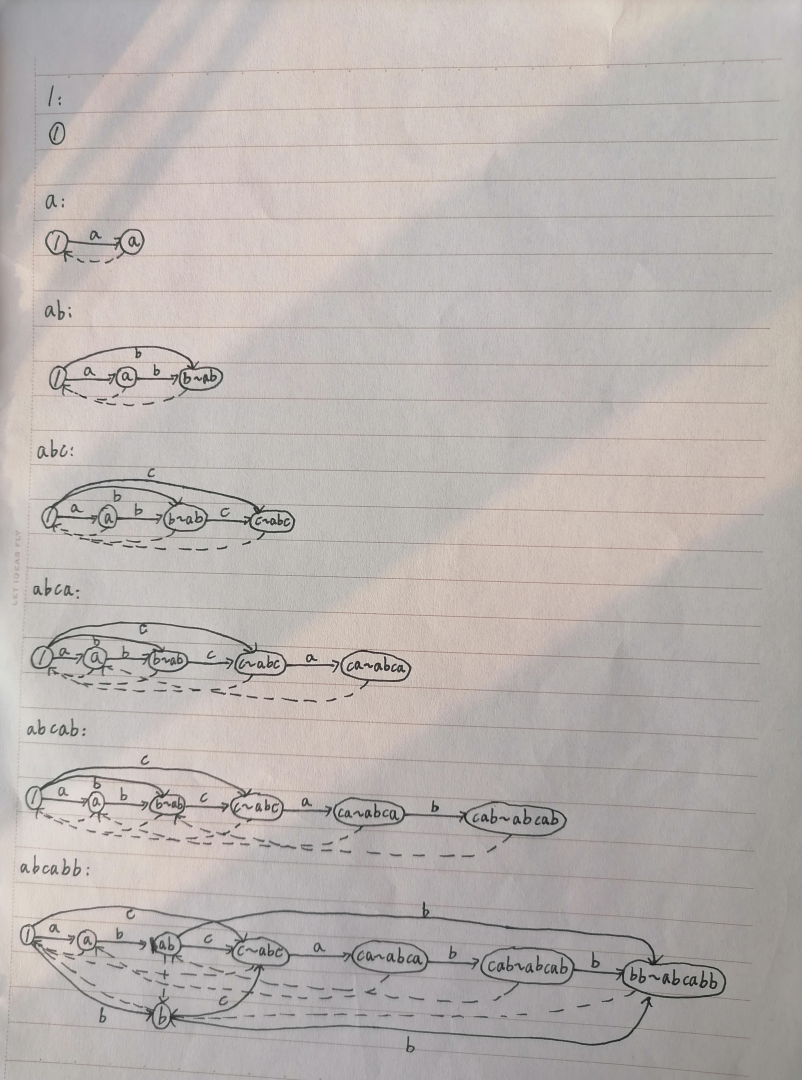
性质
从空串开始的所有转移得到的串是原串的子串(本质不同)
状态数不会超过 \(2n-1\),转移数不会超过 \(3n-4\)。设 \(\text{len}(x)\) 表示状态 \(x\) 能接受的最长的字符串,则状态 \(x\) 能接受的最短的字符串数量为 \(\text{len}(\text{link}(x))+1\),同样的,状态 \(x\) 能够接受 \(\text{len}(x)-\text{len}(\text{link}(x))\) 种字符串。
我们把每次插入时创建的新状态称作“主状态”,例如,若 \(S=\mathtt{abc}\),则主状态链即为 \(\varnothing\to\mathtt{a}\to\mathtt{ab}\to\mathtt{abc}\)(此处只选出一个状态的最长字符串作为代表串)。
有两个很强大的性质:
- 对于一个状态,从它开始不断跳后缀链接,得到的后缀链接链中的所有状态中的所有字符串一定是状态代表串的后缀。
- 任何一个主状态都是原串的一个前缀。
结合这两条,我们可以发现:
从一个主状态开始不断跳后缀链接,得到的状态的字符串都是主状态的后缀,即原串前缀的后缀,即原串的子串(位置不同)。
所以我们从每个主状态开始不断跳后缀链接,得到的就是原串的所有子串,且不重不漏。
举个例子:
对于 \(S=\mathtt{abcbac}\)(它对应的 SAM 在上图已出现过),我们把所有主状态的后缀链接链写出来:
可以发现,这些字符串刚好一一对应着原串的所有子串。由这种方法,我们就可以得到所有状态的 \(\text{endpos}\) 的大小了。
(你说为什么 \(\mathtt{a}\) 出现了两次?因为它在原串中出现了两次。位置不同本质相同被认为是不同的。)
应用
检查字符串是否出现在原串中
直接照着转移边转移,看最后能不能完成所有转移即可。
查询字符串在原串中的出现次数
可以按照上文的性质预处理出每个状态的出现次数,直接求出 \(|\text{endpos}(x)|\) 即可。
不同子串个数
状态 \(x\) 刚好有 \(\text{len}(x)-\text{len}(\text{link}(x))\) 个子串,由于不重不漏,把所有状态的子串数加起来即可。
trick:对于当前字符串,在它的末尾加一个字符,不同子串个数变化量正好是 \(\text{len}(x)-\text{len}(\text{link}(x))\),其中 \(x\) 是新添加的主状态(可感性理解)。
例题:P2408 不同子串个数,P4070 [SDOI2016]生成魔咒
所有不同子串总长度
状态 \(x\) 刚好包含 \(l=\text{len}(\text{link}(x))+1\) 到 \(r=\text{len}(x)\) 之间长度的所有不重子串,因此它的贡献即为 \(\dfrac{(l+r)(r-l+1)}{2}\)。
字典序第 \(k\) 大子串
不能再用 \(\text{len}(x)\) 投机取巧了,考虑 SAM 最本质的应用:由转移可以得到所有子串。
由于 SAM 是一张 DAG,所以可以 dp,设 \(d_x\) 表示从状态 \(x\) 开始能得到多少本质不同的子串,那么有:
同样的,位置不同的子串转移为:
那么就可以贪心的去找第 \(k\) 大了。
例题:P3975 [TJOI2015]弦论,SUBLEX - Lexicographical Substring Search



 浙公网安备 33010602011771号
浙公网安备 33010602011771号