P1737 [NOI2016] 旷野大计算 题解

牛逼逼题。

Subtask 1

有手就行。

void Subtask1() {
  E x, y;
  cin >> x >> y;
  cout << -((x + y) << 1);
}

Subtask 2

同上。

void Subtask2() {
  E x;
  cin >> x;
  cout << S(-(x + (x << 4)));
}

Subtask 3

不是有手就行了。

读一遍题面，可以发现两句很重要的话：

每个跳蚤的计算能力都是有限的，他们仅可以精确到十进制小数点后 \(90\) 位，超过的部分将会被四舍五入。同理，上述表格中的操作数 \(c\) 的小数部分也不能超过 \(90\) 位。

如果在代入某一组输入数据时：你构造的计算机的计算过程中，某个计算节点的计算结果的绝对值超过 \(10^{1000}\)，则得 \(0\) 分；

给了这么高的精度，spj 限制却只有 \(10^{-9}\)，肯定要干一些奇奇怪怪的事情把精度炸掉。

考虑 \(S(x)\) 的图像：

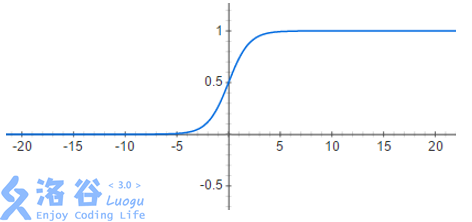
可以发现，这个函数在左右两端都存在极限，换句话说，\(\displaystyle\lim_{x\to\infty}S(x)=1\)，\(\displaystyle\lim_{x\to-\infty}S(x)=0\)，且 \(S(0)=\dfrac{1}{2}\)。

不难想到，我们可以通过左移一个较大的数使得 \(S(x)\) 爆掉精度（类似取极限），从而得到一个分段函数：

\[S(x\cdot2^k)= \begin{cases} 1 & x>0\\ \frac{1}{2} & x=0\\ 0 & x<0 \end{cases} \]

此函数非常重要，可以给它单独提出来，即 \(P(x)=S(x\cdot2^k)\)。

将这个函数乘二再减一就是 Subtask3 的答案了。

E P(E x) {  // <0: 0, =0: 1/2, >0: 1
  return S(x << 150);
}
E Sign(E x) {
  return (P(x) << 1) + "-1";
}
void Subtask3() {
  E x;
  cin >> x;
  cout << Sign(x);
}

Subtask 4

有点难度。

考虑 \(S'(x)\)，经过一些计算可以得到它的解析式为 \(\dfrac{e^x}{(e^x+1)^2}\)，值域为 \([0,\dfrac{1}{4}]\)，而且有 \(S'(0)=\dfrac{1}{4}\)。

通过一些数学知识，我们能够知道直线 \(\dfrac{1}{2}+\dfrac{1}{4}x\) 能够在 \(0\) 附近较好的拟合 \(S(x)\)。

所以我们可以把 \(x\) 右移一个较大的数让他变成无穷小，再把它丢进 \(S(x)\) 里面，得到：

\[\lim_{k\to\infty}S(\frac{x}{2^k})=\frac{1}{2}+\frac{x}{2^{k+2}} \]

把它减去 \(\dfrac{1}{2}\) 再加上 \(2^{k+2}\)，我们就由 \(S(\dfrac{x}{2^k})\) 求出了 \(x\) 的值。

但是这不是一个分段函数，我们希望它的值能在 \(x>0\) 和 \(x<0\) 的时候能有显著不同。

哪里有一个这样的数呢？

你猜猜为啥我要在上面说 \(P(x)\) 很重要。

把 \(P(x)\) 左移一个较大的数，得到：

\[P(x)\cdot2^k=\begin{cases} 2^k & x>0\\ 2^{k-1} & x=0\\ 0 & x<0 \end{cases} \]

把这个数加到 \(S(x)\) 的参数里面，得到：

\[S(\frac{x}{2^k}+P(x)\cdot2^p)=\begin{cases} 1 & x\geq0\\ \dfrac{1}{2}+\dfrac{x}{2^{k+2}} & x<0 \end{cases} \]

减去 \(\dfrac{1}{2}\) 再乘上 \(2^{k+2}\)，我们有：

\[2^{k+2}(S(\frac{x}{2^k}+P(x)\cdot2^p)-\frac{1}{2})=\begin{cases} 2^{k+1} & x\geq0\\ x & x<0 \end{cases} \]

这时需要开一点脑洞，把这个式子再减去一个 \(P(x)\cdot2^{k+1}\)，我们得到：

\[2^{k+2}(S(\frac{x}{2^k}+P(x)\cdot2^p)-\frac{1}{2})-P(x)\cdot2^{k+1}=\begin{cases} 0 & x>0\\ 2^k & x=0\\ x & x<0 \end{cases} \]

但是 \(x=0\) 又出来了，这让我们很不爽，怎么办呢？

每个跳蚤的计算能力都是有限的，他们仅可以精确到十进制小数点后 \(90\) 位，超过的部分将会被四舍五入。同理，上述表格中的操作数 \(c\) 的小数部分也不能超过 \(90\) 位。

我们直接把 \(x\) 加上一个 SPJ 精度外的 \(\epsilon\)，使得它不会取到 \(0\) 就行了。

最后得到的是一个 \(\min(x,0)\)，乘二后被 \(x\) 减一下就是 \(|x|\) 了。

具体实现中可以取 \(p=k+1\)，这样就可以省去一次位移了。

需要一定的常数优化。

const string kEps = "0." + string(20, '0') + "1";
E Min0(E x) {  // min(x, 0)
  E p = P(x + kEps) << 151;
  E y = S((x >> 150) + p);
  return ((y + "-0.5") << 152) - p;
}
E Abs(E x) {
  E p = P(x + kEps) << 152;
  E y = S((x >> 150) + p);
  return x - ((y + "-0.5") << 153) + p;
}
void Subtask4() {
  E x;
  cin >> x;
  cout << Abs(x);
}

Subtask 5

在领略了一番极限之美后，终于又来了一道送分题。

直接秦九韶即可，注意避免不必要的位移。

void Subtask5() {
  E s;
  cin >> s;
  for (int i = 0; i < 31; ++i) {
    E x;
    cin >> x;
    s = (s << 1) + x;
  }
  cout << s;
}

Subtask 6

对于某一位 \(i\)，我们本质上需要实现一个比较运算符来比较 \(2^i\) 和 \(a\)。

我们又可以用到万能的 \(P(x)\)。

直接代入 \(P(a-2^i+\epsilon)\)，我们就求出了 \(a\) 和 \(2^i\) 的大小关系。

把这一位左移后从 \(a\) 中减去即可。

注意避免不必要的位移。

常数优化：我们可以打表出 \(2^k(-2^i+\epsilon)\)，同时在最开始把 \(a\) 左移 \(k\) 位。这样可以在每一位上省去一次位移和一次加法。注意在最后要把 \(a\) 右移回来。

string kP[32] = {
    // (-2^i+1e-10)*2^50
    "",
    "-2251799813572658.0093157376",
    "-4503599627257906.0093157376",
    "-9007199254628402.0093157376",
    "-18014398509369394.0093157376",
    "-36028797018851378.0093157376",
    "-72057594037815346.0093157376",
    "-144115188075743282.0093157376",
    "-288230376151599154.0093157376",
    "-576460752303310898.0093157376",
    "-1152921504606734386.0093157376",
    "-2305843009213581362.0093157376",
    "-4611686018427275314.0093157376",
    "-9223372036854663218.0093157376",
    "-18446744073709439026.0093157376",
    "-36893488147418990642.0093157376",
    "-73786976294838093874.0093157376",
    "-147573952589676300338.0093157376",
    "-295147905179352713266.0093157376",
    "-590295810358705539122.0093157376",
    "-1180591620717411190834.0093157376",
    "-2361183241434822494258.0093157376",
    "-4722366482869645101106.0093157376",
    "-9444732965739290314802.0093157376",
    "-18889465931478580742194.0093157376",
    "-37778931862957161596978.0093157376",
    "-75557863725914323306546.0093157376",
    "-151115727451828646725682.0093157376",
    "-302231454903657293563954.0093157376",
    "-604462909807314587240498.0093157376",
    "-1208925819614629174593586.0093157376",
    "-2417851639229258349299762.0093157376",
};
void Subtask6() {
  E x;
  cin >> x;
  x = x << 50;
  for (int i = 31; i > 0; --i) {
    E v = S(x + kP[i]);
    cout << v;
    x = x - (v << i + 50);
  }
  cout << (x >> 50);
}

Subtask 7

主要思路：异或是二进制里不进位的加法。

所以可以先把 \(a\) 和 \(b\) 加在一起，然后一位位看哪里是不需要进位的，减掉就行。

考虑怎么求出某一位有没有进位。

对于第 \(i\) 位而言，我们把 \(a_i\)（表示 \(a\) 二进制表示下的第 \(i\) 位）和 \(b_i\)（同 \(a_i\)）加在一起，如果为 \(2\) 就说明有一次进位。

直接判断这一位和 \(1.5\) 的大小关系即可。具体判断方法在 Subtask 6 里讲了。

注意由于本题的大小比较不可能出现相等的情况，所以不需要加 \(\epsilon\)。

E operator^(E x, E y) {
  E s = x + y;
  x = x << 50, y = y << 50;
  for (int i = 31; i > 0; --i) {
    E vx = S(x + kP[i]), vy = S(y + kP[i]);
    s = s - (P(vx + vy + "-1.5") << i + 1);
    x = x - (vx << i + 50), y = y - (vy << i + 50);
  }
  s = s - (P(x + y + "-1.5") << 1);
  return s;
}
void Subtask7() {
  E x, y;
  cin >> x >> y;
  cout << (x ^ y);
}

Subtask 8

变成连续的了，用不到 \(P(x)\) 了。

参考 Subtask 4，由于 \(S'(x)\in[0,\dfrac{1}{4}]\)，由直觉一些数学知识可知，必然存在一个 \(x\) 使得 \(S'(x)=\dfrac{1}{10}\)，设这个点为 \(\zeta\)。

那么我们知道直线 \(S'(\zeta)(x-\zeta)+S(\zeta)\) 在 \(\zeta\) 附近是能够较好的拟合 \(S(x)\) 的。

考虑把 \(a\) 右移若干位，让它变成一个很小的数，再加上 \(\zeta\)，由于这个数很接近 \(\zeta\)，所以我们可以认为 \(S(\dfrac{a}{2^k}+\zeta)=\dfrac{a}{10\cdot 2^k}+S(\zeta)\)，把它减去 \(S(\zeta)\) 后再左移回来就行。

那么问题就只剩怎么求 \(\zeta\) 了。

考虑推式子：

\[\frac{e^x}{(e^x+1)^2}=\frac{1}{10} \]

设 \(t=e^x\)。

\[\frac{t}{t^2+2t+1}=\frac{1}{10}\\ t^2+2t+1=10t\\ t^2-8t+1=0 \]

使用求根公式，得：

\[t=4\pm\sqrt{15} \]

取正数解，得：

\[t=4+\sqrt{15}\\ \zeta=x=\ln(4+\sqrt{15}) \]

使用 wolframalpha 可以得到：

\[\zeta=2.0634370688955605467272811726201318714565914498833924998360326927... \]

且

\[S(\zeta)=0.8872983346207416885179265399782399610832921705291590826587573766... \]

当然用 python+checker 也是可以的。

void Subtask8() {
  string kV = "2.0634370688955605467272811726201318714565914498833924998360326927";
  string kS = "-0.8872983346207416885179265399782399610832921705291590826587573766";
  E x;
  cin >> x;
  cout << ((S((x >> 150) + kV) + kS) << 150);
}

Subtask 9

排序本身的算法可以使用冒泡排序、插入排序、双调排序等，重点在于怎么实现比较器。

考虑一种比较独特的方法：

v = a + b
b = v - b
a = v - b

这种方法的优点就是很好改造，如果我们不想要交换，就可以这么写：

v = a + b
b = v - a
a = v - b

具体的，我们规定，如果 \(a<b\) 就不交换，否则交换。那么代码就会长这样：

v = a + b
b = v - min(a, b)
a = v - b

而我们在 Subtask 4 中弄出来了个 \(\min(x,0)\)，那么我们就可以通过这种方式把 \(\min(a,b)\) 弄出来：

min(a, b) = min(a - b, 0) + b

嵌入到代码中，可以得到：

v = a + b
b = a - min(a - b, 0)
a = v - b

没了。

双调排序的教程可以看巨佬紫钦的博客。

void Cmp(E &x, E &y) {
  E v = x + y;
  y = x - Min0(x - y), x = v - y;
}
void Subtask9() {
  E a[16];
  for (int i = 0; i < 16; ++i) {
    cin >> a[i];
  }
  // 双调排序
  for (int i = 2; i <= 16; i <<= 1) {
    for (int j = 0; j < 16; ++j) {
      if (j < (j ^ (i - 1))) {
        Cmp(a[j], a[j ^ (i - 1)]);
      }
    }
    for (int j = i >> 2; j; j >>= 1) {
      for (int k = 0; k < 16; ++k) {
        if (k < (k ^ j)) {
          Cmp(a[k], a[k ^ j]);
        }
      }
    }
  }
  for (int i = 0; i < 16; ++i) {
    cout << a[i];
  }
}

Subtask 10

首先乘法和取模我们是绕不开了。考虑怎么实现这两玩意。

乘法

考虑使用快速幂的思想，把 \(b\) 按二进制拆位，那么我们就只要实现一个数和一个只可能为 \(0\) 或 \(1\) 的数的乘法了。不妨设前一个数为 \(x\)，后一个数为 \(y\)。

首先把 \(y\) 减一造出正负的不同。按套路把这个数左移成能显著影响 \(S(x)\) 的无穷大后加到 \(\dfrac{x}{2^k}\) 上，此时这个函数就变成了一个分段函数：

\[S(\frac{x}{2^k}+(y-1)\cdot2^p)= \begin{cases} 0 & y=0\\ \dfrac{1}{2}+\dfrac{x}{2^{k+2}} & y=1 \end{cases} \]

减去 \(\dfrac{1}{2}\)，乘上 \(2^{k+2}\)，不妨设 \(p=k+1\)，此时可以直接减去 \((y-1)\cdot2^p\) 来把 \(y=0\) 时多算的部分减掉。我们就求出了 \(x\cdot y\)。

取模

考虑倍增。

由于 \(a,b<2^{32}\)，所以结果不会超过 \(2^{64}\)，从高到低枚举每一位，看当前乘积和 \(m\cdot 2^i\) 的大小关系即可。

注意不必要的位移。

E Mul0(E x, E y) {  // y=0/1
  E p = (y + "-1") << 151;
  E v = S((x >> 150) + p);
  return ((v + "-0.5") << 152) - p;
}
E operator*(E x, E y) {
  E s = x >> 1000;
  y = y << 50;
  for (int i = 31; i > 0; --i) {
    E v = S(y + kP[i]);
    s = s + Mul0(x << i, v);
    y = y - (v << i + 50);
  }
  s = s + Mul0(x, y >> 50);
  return s;
}
E operator%(E x, E m) {
  for (int i = 63; i > 0; --i) {
    x = x - Mul0(m << i, S((x - (m << i) + kEps) << 500));
  }
  x = x - Mul0(m, S((x - m + kEps) << 500));
  return x;
}
void Subtask10() {
  E a, b, m;
  cin >> a >> b >> m;
  cout << a * b % m;
}

全部代码见这里。