莫队

对于区间修改，区间查询，我们知道有线段树(链状)，RMQ，树状数组，分块，树剖(树形结构)...尽管它们很优秀，但是在处理一些区间问题上，仍然有所不足。

事实上，如果题目不要求在线，存在一种及其优秀的算法：莫队。

什么是莫队？

转载请注明出处，部分内容引自ouuan大神的博客。

莫队是一种基于分块思想的离线算法，用于解决区间问题，适用范围如下：

　　1.只有询问没有修改

　　2.允许离线

　　3.在已知询问 [l,r] 答案的情况下可以O(1)得到

　　 [l,r-1],[l,r+1],[l-1,r],[l+1,r] 的答案。

可离线、无修改的莫队

莫队算法其实我们并不陌生，大家在处理区间问题时或多或少使用过莫队的思想。

莫队算法的精髓就是通过合理地对询问排序，并把询问的结果作为下一个询问求解的基础，使得暴力求解的复杂度得到保证。

eg:[国家集训队]小Z的袜子

在此题中，用 cnt[i] 表示当前处理的区间内颜色为 i 的袜子出现的次数，用 len 表示当前处理的区间的长度，用 x 表示新增的那只袜子的颜色。

以已知区间 [l,r] 的答案求解区间 [l,r+1] 为例。分别处理分子和分母：

分母为任选两只袜子的组合总数，原先是 len*(len-1)/2，现在是 len*(len+1)/2，增加了len。
分子为两只袜子颜色相同的组合总数，比原来增加了 cnt[i]，即新增的这只袜子和原本就在当前区间内的相同颜色的袜子的组合。

因此，将一只颜色为 x 的袜子计入答案的函数就可以写出来了：

add

void add(int x){
    fz+=cnt[x];
    ++cnt[x];
    fm+=len;
    ++len;
}

同理，我们可以求得将一只袜子移出袜子的函数：

del

void del(int x){
    --cnt[x];
    fm-=cnt[x];
    --len;
    fz-=len;
}

于是，我们就可以得到一个暴力的算法：用 l 和 r 分别记录当前区间的两个端点，然后用下面这段代码来更新答案。

while(l>q[i].l) add(col[--l]);
while(r<q[i].r) add(col[++r]);
while(l<q[i].l) del(col[l++]);
while(r>q[i].r) del(col[r--]);

那么，现在我们根据题目询问将区间不断左移或者右移得出答案。这样的时间复杂度是O(mn)。此时我们想一想，既然询问是离线的，我们是否可以将询问合理的排序，确保 l,r 走过的总距离最短。

那么问题来了：什么是“合理的排序”？

假设题目给了许多个查询区间，为了保证每个点被重复的次数最少，我们先按照区间左端点从小到大排序；如果左端点相同，那么按照右端点从小到大排序。

这样似乎已经是很好的排序方案了。仔细想想其实不然，左端点不会“回车”，右端点未必，假设右端点时不时“回车”，这样比起一般暴力，并没有优化多少。

我们的目的是使 l,r 走过的总距离最短，这时候一种新的算法登场了——分块。

运用分块的思想，将整个区间 [1,n] 分成若干块，以询问的左端点所在块为第一关键字，以询问右端点的大小为第二关键字，对询问进行排序，那么：

对于同一块的询问，l 指针最多移动单位块(B)的的大小，r 指针的移动是单调的，总共移动最多n。
对于不同块的询问，l 每次换块时最多移动两个单位块(B)的大小，总共移动最多n，r 每次换块最多移动n。

总结：l 指针每次最多移动O(B)，r指针每块移动O(n)。

所以：

l 的移动次数最多为询问数 m *块的大小 B，即O(mB)。
r 的移动次数最多为块的个数 n/B *总区间大小 n，即O(n²/B)。

因此，总移动次数为O(mB+n²/B)。

这是什么？对勾函数。

显然，当B=时复杂度最小，为O()。（有疑问的同学可以求导证明）。

剩下最后一个问题：初始的当前区间是什么？

只要指定任意一个空区间就好了，如 l=1,r=0。

所以，整个莫队算法就可以概括为：

将询问记录下来。
以为块的大小，以询问的左端点所在块为第一关键字，右端点为第二关键字，对询问进行排序。
暴力处理每个询问。
输出答案。

总的复杂度为O()。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,m,t,fz,fm,len,B;
int col[N],cnt[N],ans[N][2];
struct query{
    int l,r,id;
}q[N];
bool cmp(query a, query b){
    return a.l/B==b.l/B?a.r<b.r:a.l<b.l;
}
void add(int x){
    fz+=cnt[x];
    ++cnt[x];
    fm+=len;
    ++len;
}
void del(int x){
    --cnt[x];
    fz-=cnt[x];
    --len;
    fm-=len;
}
int main(){
    cin>>n>>m;
    B=n/sqrt(m);
    for(int i=1;i<=n;++i) cin>>col[i];
    for(int i=1;i<=m;++i) cin>>q[i].l>>q[i].r,q[i].id=i;
    sort(q+1,q+1+m,cmp);
    int l=1,r=0;
    for(int i=1;i<=m;++i){
        if(q[i].l==q[i].r){
            ans[q[i].id][0]=0;
            ans[q[i].id][1]=1;
            continue;
        }
        while(l>q[i].l) add(col[--l]);
        while(r<q[i].r) add(col[++r]);
        while(l<q[i].l) del(col[l++]);
        while(r>q[i].r) del(col[r--]);
        int x=__gcd(fz,fm);
        ans[q[i].id][0]=fz/x;
        ans[q[i].id][1]=fm/x;
    }
    for(int i=1;i<=m;++i) cout<<ans[i][0]<<'/'<<ans[i][1]<<'\n';
    return 0;
}

带修莫队

前面说过，普通的莫队只能解决没有修改的问题，那么带修改的问题怎么解决呢？带修莫队就是一种支持单点修改的莫队算法。

算法简介

还是对询问进行排序，每个询问除了左端点和右端点还要记录这次询问是在第几次修改之后(时间)，以左端点所在快为第一关键字，以右端点所在块为第二关键字，以时间为第三关键字进行排序。

暴力查询时，如果当前修改数比询问的修改数少就把没修改的进行修改，反之回退。

需要注意的是，修改分为两部分：

若修改的位置在当前区间内，需要更新答案(del原颜色，add修改后的颜色)。
无论修改的位置是否在当前区间内，都要进行修改(以供add和del函数在以后更新答案)。

分块大小的选择以及复杂度证明

(用B表示分块大小，c表示修改个数，q表示询问个数，l块表示以L/B分的块，r块表示以R/B分的块，每个l块包含n/B个r块)

对于时间指针now：对于每个r块，最坏情况会移动c，共有(n/B)²个r块，所以总移动次数为。
对于左端点指针l：l块内移动每次最多B，换l块每次最多2B，所以总移动次数为O(qB)。
对于右端点指针r：r块内移动每次最多B，换r块每次最多2B，所有l块内移动次数之和为O(qB)；换l块时最多移动n，总的换l块时移动次数为O(n²/B)；所以总的移动次数为O(qB+n²/B)。

所以，总的移动次数为O()。

由于一般的题目都不会告诉你修改和询问分别的个数，所以统一用m来表示，即O()。

那么B取多少呢...Mathematica告诉我大概是这个

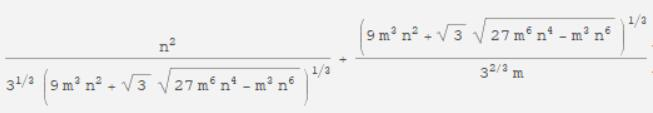
(略显复杂，我们仍然只考虑最重要的因子)。

由于B由n和m共同影响，感兴趣的同学们可以自行求出最佳分块。

暂时不纠结带修莫队的最佳分块大小好了...视作 n=m 的话，就可以得到总移动次数为O()，那么B=n^2/3时取最小值O()。

所以，带修莫队的渐进时间复杂度为O(nlogn+n^5/3)。

eg:[国家集训队]数颜色

代码

#include <bits/stdc++.h>
using namespace std;
void add(int x);
void del(int x);
void modify(int x,int ti);  //这个函数会执行或回退修改ti（执行还是回退取决于是否执行过，具体通过swap实现），x表明当前的询问是x，即若修改了区间[q[x].l,q[x].r]便要更新答案
int n,m,B,cnt[1000010],a[50010],ans,ccnt,qcnt,now,out[50010];
struct Change
{
    int p,col;
} c[50010];
struct Query
{
    int l,r,t,id;
    bool operator<(Query& b)
    {
        return l/B==b.l/B?(r/B==b.r/B?t<b.t:r<b.r):l<b.l;
    }
} q[50010];
int main()
{
    int i,l=2,r=1;
    char type[10];    
    cin>>n>>m;
    B=pow(n,0.66666);
        
    for (i=1;i<=n;++i) cin>>a[i];
    
    for (i=1;i<=m;++i)
    {
        scanf("%s",type);
        if (type[0]=='Q')
        {
            ++qcnt;
            cin>>q[qcnt].l>>q[qcnt].r;
            q[qcnt].t=ccnt;
            q[qcnt].id=qcnt;
        }
        else
        {
            ++ccnt;
            cin>>c[ccnt].p>>c[ccnt].col;
        }
    }
    
    sort(q+1,q+qcnt+1);
    
    for (i=1;i<=qcnt;++i)
    {
        while (l>q[i].l)
        {
            add(a[--l]);
        }
        while (r<q[i].r)
        {
            add(a[++r]);
        }
        while (l<q[i].l)
        {
            del(a[l++]);
        }
        while (r>q[i].r)
        {
            del(a[r--]);
        }
        while (now<q[i].t)
        {
            modify(i,++now);
        }
        while (now>q[i].t)
        {
            modify(i,now--);
        }
        out[q[i].id]=ans;
    }
    
    for (i=1;i<=qcnt;++i)
    {
        cout<<out[i]<<endl;
    }
    
    return 0;
}

void add(int x)
{
    if (cnt[x]++==0)
    {
        ++ans;
    }
}

void del(int x)
{
    if (--cnt[x]==0)
    {
        --ans;
    }
}

void modify(int x,int ti)
{
    if (c[ti].p>=q[x].l&&c[ti].p<=q[x].r)
    {
        del(a[c[ti].p]);
        add(c[ti].col);
    }
    swap(a[c[ti].p],c[ti].col); //下次执行时必定是回退这次操作，直接互换就可以了 
}

树上莫队

其实，莫队算法除了序列还可以用于树。复杂度同序列上的莫队(不带修O()，带修O())。

eg.[WC2013] 糖果公园

分块方式

这里需要看一道专门为树上莫队设计的题目[SCOI2005]王室联邦。

用这道题所要求的方式进行分块，并用后文的方式更新答案，就能保证复杂度(复杂度分析见后文)。

那么如何满足每块大小在[B,3B]，块内每个点到核心点路径上的所有点都在块内呢？

这里先提供一种构造方式，再予以证明：

dfs，并创建一个栈，dfs一个点时先记录初始栈顶高度，每dfs完当前节点的一颗子树就判断栈内（相对于刚开始dfs时）新增节点的数量是否>=B，是则将栈内所有新增点分为同一块，核心点为当前dfs的点，当前节点结束dfs时将当前节点入栈，整个dfs结束后将栈内所有剩余节点归入已经分好的最后一个块。

参考代码：

void dfs(int u,int fa){
    int t=top;
    for(int i=h[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dfs(v,u);
        if(top-t>=B){
            ++tot;
            while(top>t) bl[sta[top--]]=tot;
        }
    sta[++top]=u;
}
dfs(1,0);
while(top) bl[sta[top--]]=tot;

如果你看懂了这个方法的话，每块大小>=B是显然的，下面证明为何每块大小<=3B:

对于当前节点的每一颗子树：

若未被分块的节点数>B，那么在dfs这棵子树的根节点时就一定会把这颗子树的一部分分为一块直至这颗子树的剩余节点数<=B，所以这种情况不存在。
若未被分块的节点数=B，这些节点一定会和栈中所有节点分为一块，栈中之前还剩[0,B-1]个节点，那么这一块的大小为[B,2B-1]。
若未被分块的节点数<B，当未被分块的节点数+栈中剩余节点数>=B时，这一块的大小为[B,2B-1)，否则继续进行下一棵子树。

对于dfs结束后栈内剩余节点，数量一定在[1,B]内，而已经分好的每一块的大小为[B,2B-1]，所以每块的大小都在[B,3B)内。

修改方式

所谓“修改”，就是由询问（cu,cv）更新至询问（tu,tv）。

如果把两条路径上的点全部修改...显然是和暴力一样的嘛！

这里直接给出结论好了...

（下文中T(u,v)表示 u 到 v 的路径上除 lca(u,v) 外的所有点构成的集合，S(u,v)代表 u 到 v 的路径，xor表示集合对称差（就跟异或差不多））

两个指针 cu,cv（相当于序列莫队的 l,r 两个指针），ans记录T(cu,cv)的答案，vis数组记录每个节点是否在T(cu,cv)内；
由T(cu,cv)更新至T(tu,tv)时，将T(cu,tu)和T(cv,tv)的 vis 分别取反，并相应地更新答案；
将答案记录到 out 数组（离线后用于输出那个）时对 lca(cu,cv)（此时的 cu,cv 已更新为上一步中的 tu,tv）的 vis 取反并更新答案，记录完再改回来（因为lca比较烦，所以就这样做了QAQ）。

第二步证明如下：

$T (c u, c v) x o r T (t u, t v)$

关于单点修改

树上莫队的单点修改和序列莫队类似，唯一不同就是，修改后是否更新答案通过vis数组判断。

复杂度分析

每块大小在[B,3B)，所以两点间路径长度也在[B,3B)，块内移动就是O(B)的；编号相邻的块位置必然是相邻的，所以两块间路径长度也是O(B)；然后就和序列莫队的复杂度分析类似了...

eg.[WC2013]糖果公园

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>

using namespace std;

const int N=100010;

void pathmodify(int u,int v); //将T(u,v)取反并更新答案
void opp(int x); //将节点x取反并更新答案
void modify(int ti); //进行或回退修改ti
int lca(int u,int v);
void dfs(int u); //进行分块并记录dep数组、f数组（用于求lca、两点间路径）
void add(int u,int v);

int head[N],nxt[N<<1],to[N<<1],cnt;
int n,m,Q,B,bl[N],tot,V[N],W[N],a[N],sta[N],top,qcnt,ccnt,dep[N],f[20][N],num[N],now;
long long ans,out[N];
bool vis[N];

struct Query
{
    int u,v,t,id;
    bool operator<(Query& y)
    {
        return bl[u]==bl[y.u]?(bl[v]==bl[y.v]?t<y.t:bl[v]<bl[y.v]):bl[u]<bl[y.u];
    }
} q[N];

struct Change
{
    int p,x;
} c[N];

int main()
{
    int i,j,u,v,lc,type;
    
    cin>>n>>m>>Q;
    B=pow(n,0.666);
    
    for (i=1;i<=m;++i)
    {
        cin>>V[i];
    }
    
    for (i=1;i<=n;++i)
    {
        cin>>W[i];
    }
    
    for (i=1;i<n;++i)
    {
        cin>>u>>v;
        add(u,v);
        add(v,u);
    }
    
    dfs(1);
    
    for (i=1;i<=16;++i)
    {
        for (j=1;j<=n;++j)
        {
            f[i][j]=f[i-1][f[i-1][j]];
        }
    }
    
    while (top)
    {
        bl[sta[top--]]=tot;
    }
    
    for (i=1;i<=n;++i)
    {
        cin>>a[i];
    }
    
    for (i=0;i<Q;++i)
    {
        cin>>type;
        if (type==0)
        {
            ++ccnt;
            cin>>c[ccnt].p>>c[ccnt].x;
        }
        else
        {
            cin>>q[qcnt].u>>q[qcnt].v;
            q[qcnt].t=ccnt;
            q[qcnt].id=qcnt;
            ++qcnt;
        }
    }
    
    sort(q,q+qcnt);
    
    u=v=1;
    
    for (i=0;i<qcnt;++i)
    {
        pathmodify(u,q[i].u);
        pathmodify(v,q[i].v);
        u=q[i].u;
        v=q[i].v;
        while (now<q[i].t)
        {
            modify(++now);
        }
        while (now>q[i].t)
        {
            modify(now--);
        }
        lc=lca(u,v);
        opp(lc);
        out[q[i].id]=ans;
        opp(lc);
    }
    
    for (i=0;i<qcnt;++i)
    {
        cout<<out[i]<<endl;
    }
    
    return 0;
}

void pathmodify(int u,int v)
{
    if (dep[u]<dep[v])
    {
        swap(u,v);
    }
    while (dep[u]>dep[v])
    {
        opp(u);
        u=f[0][u];
    }
    while (u!=v)
    {
        opp(u);
        opp(v);
        u=f[0][u];
        v=f[0][v];
    }
}

void opp(int x)
{
    if (vis[x])
    {
        ans-=1ll*V[a[x]]*W[num[a[x]]--];
    }
    else
    {
        ans+=1ll*V[a[x]]*W[++num[a[x]]];
    }
    vis[x]^=1;
}

void modify(int ti)
{
    if (vis[c[ti].p])
    {
        opp(c[ti].p);
        swap(a[c[ti].p],c[ti].x);
        opp(c[ti].p);
    }
    else
    {
        swap(a[c[ti].p],c[ti].x);
    }
}

int lca(int u,int v)
{
    if (dep[u]<dep[v])
    {
        swap(u,v);
    }
    int i;
    for (i=0;i<=16;++i)
    {
        if ((dep[u]-dep[v])&(1<<i))
        {
            u=f[i][u];
        }
    }
    if (u==v)
    {
        return u;
    }
    for (i=16;i>=0;--i)
    {
        if (f[i][u]!=f[i][v])
        {
            u=f[i][u];
            v=f[i][v];
        }
    }
    return f[0][u];
}

void dfs(int u)
{
    int t=top;
    for (int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        if (v!=f[0][u])
        {
            f[0][v]=u;
            dep[v]=dep[u]+1;
            dfs(v);
            if (top-t>=B)
            {
                ++tot;
                while (top>t)
                {
                    bl[sta[top--]]=tot;
                }
            }
        }
    }
    sta[++top]=u;
}

void add(int u,int v)
{
    nxt[++cnt]=head[u];
    head[u]=cnt;
    to[cnt]=v;
}

莫队的拓展

posted @ 2023-03-16 20:10 青阳buleeyes 阅读(86) 评论(0) 收藏举报

刷新页面返回顶部

buleeyes

To make world better

莫队

关于单点修改

公告