【计算机组成】原码、反码、补码的使用及其原理

本篇文章讲解了计算机的原码，反码和补码。并且进行了深入探求了为何要使用反码和补码，以及更进一步的论证了为何可以用反码，补码的加法计算原码的减法。论证部分如有不对的地方请各位牛人帮忙指正! 希望本文对大家学习计算机基础有所帮助!

一. 机器数和真值

在学习原码，反码和补码之前，需要先了解机器数和真值的概念.

1、机器数

一个数在计算机中的二进制表示形式，叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号，正数为0，负数为1。

比如，十进制中的数 +3，计算机字长为8位，转换成二进制就是00000011。如果是 -3，就是 10000011 。

那么，这里的 00000011 和 10000011 就是机器数。

2、真值

因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 10000011，其最高位1代表负，其真正数值是 -3 而不是形式值131（10000011转换成十进制等于131）。所以，为区别起见，将带符号位的机器数对应的真正数值称为机器数的真值。

例：0000 0001的真值 = +000 0001 = +1，1000 0001的真值 = –000 0001 = –1

二. 原码、反码、补码的基础概念和计算方法

在探求为何机器要使用补码之前，让我们先了解原码、反码和补码的概念。对于一个数，计算机要使用一定的编码方式进行存储。原码、反码、补码是机器存储一个具体数字的编码方式。

码	数值1	数值-1	1+(-1)（将数值1和数值-1相加）
原码	0000 0001	1000 0001	1000 0010
反码	0000 0001	1111 1110	1111 1111
补码	0000 0001	1111 1111	0000 0000
移码	1000 0001	0111 1111	1000 0000

1. 原码

原码就是符号位加上真值的绝对值，即用第一位表示符号，其余位表示值。比如如果是8位二进制：

\([+1]_原 = 0000 0001\)

\([-1]_原 = 1000 0001\)

第一位是符号位。因为第一位是符号位，所以8位二进制数的取值范围就是：

[1111 1111 ，0111 1111]

即

[-127 ，127]

原码是人脑最容易理解和计算的表示方式。

2. 反码

反码的表示方法是：

• 正数的反码是其本身

• 负数的反码是在其原码的基础上，符号位不变，其余各个位取反。

\([+1] = [00000001]_原 = [00000001]_反\)

\([-1] = [10000001]_原 = [11111110]_反\)

可见如果一个反码表示的是负数，人脑无法直观的看出来它的数值，通常要将其转换成原码再计算。

3. 补码

补码的表示方法是：

• 正数的补码就是其本身

• 负数的补码是在其原码的基础上，符号位不变，其余各位取反，最后+1。 (即 在反码的基础上+1)

\([+1] = [00000001]_原 = [00000001]_反 = [00000001]_补\)

\([-1] = [10000001]_原 = [11111110]_反 = [11111111]_补\)

对于负数，补码表示方式也是人脑无法直观看出其数值的。通常也需要转换成原码在计算其数值。

三. 为何要使用原码，反码和补码

在开始深入学习前，我的学习建议是先"死记硬背"上面的原码，反码和补码的表示方式以及计算方法。

现在我们知道了计算机可以有三种编码方式表示一个数。对于正数因为三种编码方式的结果都相同：

\([+1] = [00000001]_原 = [00000001]_反 = [00000001]_补\)

所以不需要过多解释。但是对于负数：

\([-1] = [10000001]_原 = [11111110]_反 = [11111111]_补\)

可见原码，反码和补码是完全不同的. 既然原码才是被人脑直接识别并用于计算表示方式，为何还会有反码和补码呢?

首先，因为人脑可以知道第一位是符号位，在计算的时候我们会根据符号位，选择对真值区域的加减. (真值的概念在本文最开头). 但是对于计算机，加减乘数已经是最基础的运算，要设计的尽量简单. 计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法. 我们知道，根据运算法则减去一个正数等于加上一个负数，即: 1-1 = 1 + (-1) = 0 ，所以机器可以只有加法而没有减法，这样计算机运算的设计就更简单了.

于是人们开始探索 将符号位参与运算，并且只保留加法的方法. 首先来看原码:

计算十进制的表达式: 1-1=0

\(1 - 1 = 1 + (-1) = [00000001]_原 + [10000001]_原 = [10000010]_原 = -2\)

如果用原码表示，让符号位也参与计算，显然对于减法来说，结果是不正确的.这也就是为何计算机内部不使用原码表示一个数.

为了解决原码做减法的问题，出现了反码:

计算十进制的表达式: 1-1=0

\(1 - 1 = 1 + (-1) = [0000 0001]_原 + [1000 0001]_原 = [0000 0001]_反 + [1111 1110]_反 = [1111 1111]_反 = [1000 0000]_原 = -0\)

发现用反码计算减法，结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的，但是0带符号是没有任何意义的. 而且会有[0000 0000]_原和[1000 0000]_原两个编码表示0.

于是补码的出现，解决了0的符号以及两个编码的问题:

\(1-1 = 1 + (-1) = [0000 0001]_原 + [1000 0001]_原 = [0000 0001]_补 + [1111 1111]_补 = [0000 0000]_补 =[0000 0000]_原\)

这样0用[0000 0000]表示，而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:

\((-1) + (-127) = [1000 0001]_原 + [1111 1111]_原 = [1111 1111]_补 + [1000 0001]_补 = [1000 0000]_补\)

-1-127的结果应该是-128，在用补码运算的结果中，\([1000 0000]_补\) 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128，所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是\([0000 0000]_原\) ，这是不正确的)

使用补码，不仅仅修复了0的符号以及存在两个编码的问题，而且还能够多表示一个最低数. 这就是为什么8位二进制，使用原码或反码表示的范围为\([-127，+127]\)，而使用补码表示的范围为\([-128，127]\)。

因为机器使用补码，所以对于编程中常用到的32位int类型，可以表示范围是: \([-2^{31}，2^{31}-1]\) 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.

总结：

• 原码：数值的原二进制数值
• 反码：解决了减法转化为加法的问题。

  遗留问题：存在正负两种0数值

  • +0：\([0000 0000]_反\)
  • -0：\([1000 0000]_反\)

• 补码：解决了+0和-0的问题

  • \([0000 0000]_补\)：0
  • \([1000 0000]_补\)：-128

四 原码，反码，补码 再深入

计算机巧妙地把符号位参与运算，并且将减法变成了加法，背后蕴含了怎样的数学原理呢?

将钟表想象成是一个1位的12进制数。如果当前时间是6点，我希望将时间设置成4点，需要怎么做呢？我们可以：

1. 往回拨2个小时：\(6 - 2 = 4\)
2. 往前拨10个小时：\((6 + 10) \pmod {12} = 4\)
3. 往前拨10+12=22个小时：\((6+22) \pmod {12} =4\)

2,3方法中的mod是指取模操作，\(16 \pmod {12} = 4\)，即 用16除以12后的余数是4。

所以钟表往回拨(减法)的结果可以用往前拨(加法)替代！

现在的焦点就落在了如何用一个正数，来替代一个负数。上面的例子我们能感觉出来一些端倪，发现一些规律。但是数学是严谨的，不能靠感觉。

首先介绍一个数学中相关的概念：同余

同余的概念

两个整数a，b，若它们除以整数m所得的余数相等，则称a，b对于模m同余

记作 \(a ≡ b \pmod m\)

读作 a 与 b 关于模 m 同余。

举例说明:

\(4 \pmod {12} = 4\)

\(16 \pmod {12} = 4\)

\(28 \pmod {12} = 4\)

所以4，16，28关于模 12 同余.

负数取模

正数进行mod运算是很简单的. 但是负数呢?

下面是关于mod运算的数学定义:

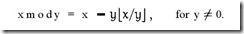
⌊ x / y ⌋为取下界符号，取底

\[x \pmod y = x - y ⌊ x / y ⌋ \]

上面公式的意思是:

x mod y等于 x 减去 y 乘上 x与y的商的下界.

以 -3 mod 2 举例:

-3 mod 2

= -3 - 2 x ⌊-3/2⌋

= -3 - 2 x ⌊-1.5⌋

= -3 - 2 x (-2)

= -3 + 4 = 1

所以:

(-2) mod 12 = 12-2=10

(-4) mod 12 = 12-4 = 8

(-5) mod 12 = 12 - 5 = 7

开始证明

再回到时钟的问题上:

回拨2小时 = 前拨10小时

回拨4小时 = 前拨8小时

回拨5小时= 前拨7小时

注意，这里发现的规律!

结合上面学到的同余的概念.实际上:

\((-2) \pmod {12} = 10\)

\(10 \pmod {12} = 10\)

-2与10是同余的.

\((-4) \pmod {12} = 8\)

\(8 \pmod {12} = 8\)

-4与8是同余的.

距离成功越来越近了. 要实现用正数替代负数，只需要运用同余数的两个定理:

反身性:

\(a ≡ a \pmod m\)

这个定理是很显而易见的.

线性运算定理:

如果\(a ≡ b \pmod m\)，\(c ≡ d \pmod m\) 那么:

(1)\(a ± c ≡ b ± d \pmod m\)

(2)\(a * c ≡ b * d \pmod m\)

如果想看这个定理的证明，请看:http://baike.baidu.com/view/79282.htm

所以:

\(7 ≡ 7 \pmod {12}\)

\((-2) ≡ 10 \pmod {12}\)

\(7 -2 ≡ 7 + 10 \pmod {12}\)

现在我们为一个负数，找到了它的正数同余数. 但是并不是7-2 = 7+10，而是 7 -2 ≡ 7 + 10 (mod 12) ，即计算结果的余数相等.

接下来回到二进制的问题上，看一下: 2-1=1的问题.

\(2-1=2+(-1) = [0000 0010]_原 + [1000 0001] _原 = [0000 0010]_反 + [1111 1110]_反\)

先到这一步，-1的反码表示是1111 1110. 如果这里将[1111 1110]认为是原码，则[1111 1110]原 = -126，这里将符号位除去，即认为是126.

发现有如下规律:

\((-1) \pmod {127} = 126\)

\(126 \pmod {127} = 126\)

即:

\((-1) ≡ 126 \pmod {127}\)

\(2-1 ≡ 2+126 \pmod {127}\)

2-1 与 2+126的余数结果是相同的! 而这个余数，正式我们的期望的计算结果: 2-1=1

所以说一个数的反码，实际上是这个数对于一个模的同余数. 而这个模并不是我们的二进制，而是所能表示的最大值! 这就和钟表一样，转了一圈后总能找到在可表示范围内的一个正确的数值!

而2+126很显然相当于钟表转过了一轮，而因为符号位是参与计算的，正好和溢出的最高位形成正确的运算结果.

既然反码可以将减法变成加法，那么现在计算机使用的补码呢? 为什么在反码的基础上加1，还能得到正确的结果?

\(2-1=2+(-1) = [0000 0010]_原 + [1000 0001]_原 = [0000 0010]_补 + [1111 1111]_补\)

如果把[1111 1111]当成原码，去除符号位，则：

\([0111 1111]_原 = 127\)

其实，在反码的基础上+1，只是相当于增加了模的值：

\((-1) \pmod {128} = 127\)

\(127 \pmod {128} = 127\)

\(2-1 ≡ 2+127 \pmod {128}\)

此时，表盘相当于每128个刻度转一轮. 所以用补码表示的运算结果最小值和最大值应该是[-128，128].

但是由于0的特殊情况，没有办法表示128，所以补码的取值范围是[-128，127]

目的：统一计算方式，简化计算机线路复杂度。
原因：借鉴数论中同余理论，设计，用补码不用反码，计算过程没有区别，但是可以多表示一个数。

本文参考：https://www.cnblogs.com/zhangziqiu/archive/2011/03/30/ComputerCode.html