Bellman_Ford

updata 2025.8.24 添加了一些 hack，说明了一些错误思想

基本上用不到的算法，和高精度一样，不常用，用到了又无可代替
常用于限制边数的最短路算法。

使用范围

可以处理任意边权的图，可以判断负环。
时间复杂度 \(O(nm)\)。因为太慢了，在求最短路的时候基本用不到，但是它的优化版 SPFA 则大大优化了时间复杂度，算是最短路里最好用的算法，有很强的适应性。但近年来容易被卡。

中心思想

对每个点进行 \(n - 1\) 轮松弛。
每一轮会遍历所有边，一共 \(n - 1\) 轮，时间复杂度也就是 \(O(nm)\)。

正确性证明

第一种：第 \(1\) 轮松弛得到的是起点到其他点，最多经过 \(1\) 条边的最短路径；第 \(n\) 轮得到的就是从起点到其他点，最多经过 \(n\) 条边点的最短路径。因为在 \(n\) 个点中，两个点之间的最短路径最多有 \(n - 1\) 条边，即对每个点最多进行 \(n - 1\) 轮松弛可以得到最短距离。
如果超过 \(n-1\) 轮还有边可以被松弛，那么说明有源点 \(S\) 点能到达的负环。

第二种：如果最短路径经过了 \(n\) 条边，那么一定有 \(n + 1\) 个点，而点数一共 \(n\) 个，所以至少有一个点被重复经过了，也就是说最短路径出现了环。对于环如果是正环，我们完全可以省略；如果是 \(0\) 权环，那么不会引起最短路的松弛，依靠我们的算法，就不会经过这个环；如果是负环，因为可以减小权值所以可行。综上只可能是负权环，而我们求最短路一般是不考虑负权环的（因为它可以让边权无限减小），所以最多只能经过 \(n - 1\) 条边。

实操步骤

1. 枚举每个点 \(u\)
2. 枚举 \(u\) 连接着的边 \(w\) 和点 \(j\)，并用和 \(dist[u]\) 和 \(w\) 更新 \(dist[j]\)
3. 循环上面过程 \(n - 1\) 次

代码

代码和思想一样
但略有不同。

int bellman_ford(int S, int T)
{
    memset(dist, 0x3f, sizeof dist);
    dist[S] = 0;
    int k = n;
    while ( -- k)
    {
        memcpy(g, dist, sizeof dist);
        for (int u = 1; u <= n; u ++ ) // 枚举每个点u
            for (int i = h[u]; i != -1; i = ne[i]) // 用u对j进行松弛操作
            {
                int j = e[i];
                dist[j] = min(dist[j], g[u] + w[i]);
            }
    }
    return dist[T];
}

可以发现代码多了一个 \(g\) 数组，\(g\) 是 \(dist\) 的复制数组，如果只是求最短路的话可以不用 \(g\) 代替 \(dist\)，但如果考虑限制经过 \(k\) 条边的话，必须加上。设当前为第\(k\)轮，那么 \(g\) 里面存的就是第 \(k - 1\) 轮的最短路，如果不这么做直接用 \(dist\) 更新，可能会出现连续更新的现象，即在这轮用刚更新完的 \(dist\) 去更新了其他点的 \(dist\)，就可能会打破边数的限制，在第 \(k\) 轮有经过 \(k + x\) 条边的最短路径，导致算法错误。因此，有必要加上这个\(g\) 数组。

扩展（必看）

判断负环

据上面所说，我们最多 \(n-1\) 轮就能得出最短路径，也就说第 \(n\) 轮的时候不可能有边还能被松弛，如果有，则说明具有负环，可以无限松弛边长。这里还要注意一点，如果是发现第 \(n\) 轮没有边被松弛，不一定图上没有负环，可能只是源点 \(S\) 到不了而已，因此判断负环时应使用一个超级源点把所有点都连起来，边权为 \(0\) ，这样才能完美地找出负环。

第 \(k\) 轮的性质

当第 \(k\) 轮结束时，得到的边是在经过不超过 \(k\) 条边的下的最短路径，而一个点在第 \(k\) 轮被更新说明什么？能引起第 \(k\) 轮更新的点，只有第 \(k-1\) 轮被更新过的点才有可能，以此类推，可知第 \(k\) 轮被更新的点，更新的最短路径中必定包含 \(k\) 条边。这是一条很重要的性质。

下面给出更详细一点的例子（如果不懂的话）：

在 Bellman_Ford 中，对与一个点 \(u\) 来说，第一轮松弛 \(u\) 可能会被松弛多次，但最短路经过的边数始终为 \(1\)，而在第二轮时，如果 \(u\) 还能被松弛，则说明，这个松弛它的点是在上一轮松弛过得（即最短路经过一条边的点），那么此时 \(u\) 的最短路经过路径为 \(2\) 条。

以此类推，如果第三轮 \(u\) 能被松弛， 那么能松弛它的点 \(j\) 一定也是上一轮松弛过得（如果这个 \(j\) 不是上一轮松弛过的，而此轮能够松弛 \(u\)，那么说明在上一轮它也可以松弛 \(u\)，但却没进行松弛，这是矛盾的，说明 \(j\) 只能是上一轮松弛过的，这个证明可以移动至任何一轮），那么它的最短路经过的边数为 \(3\) 条。由此递推，在 Bellman_Ford 算法中，在第 \(k\) 轮被松弛的点，最短路经过的边一定为 \(k\) 条。

需要注意，在第 \(k\) 轮中，\(u\) 可能会被松弛超过 \(k\) 次（即在一轮中可能会被多个点松弛）。所以在 SPFA 或者 Bellman_Ford 中单论松弛次数是无意义的（注意不是松弛轮数）。如下图：

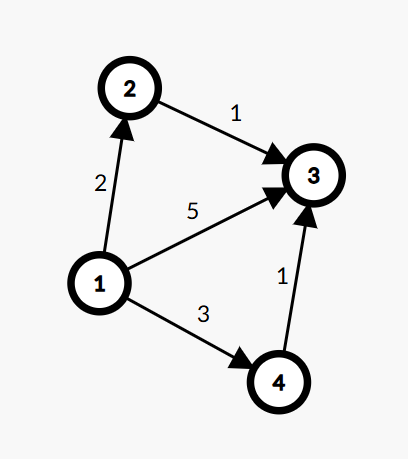
以 \(1\) 为源点，根据算法流程会第一轮先松弛 \(2,3,4\) 三个点，每个点此时都只松弛了一次，而在第二轮，如果 \(4\) 先松弛了 \(3\)，而后 2 又松弛了 \(3\)，此时在这轮，\(3\) 已经被松弛了两次，此时第 \(2\) 轮，但 \(3\) 却松弛了 \(3\) 次，最短路只经过两条边。可以看出，松弛次数和最短路经过边数并没有直接关系。

下面构造反例说明上面的正确（如果你已经懂了可以略过）。
如以下数据：

4 6 
2 3 -1
3 4 3
2 4 4
1 3 1
1 4 10
1 2 1

构造如图：

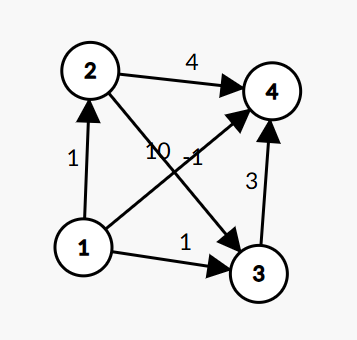
图中并无负环，但 \([1,4]\) 四个点的松弛次数却分别为：\(0,1,2,4\) 存在松弛此时等于 \(n\) 的情况，但是图中并没有负环。说明，松弛次数为 \(n\) 并不一定经过 \(n\) 条边（即不一定存在负环），Bellman_Ford 算法中每个点不一定最多松弛 \(n - 1\) 次。这也可以证明松弛次数和最短路边数没有直接关系。有关系的只有轮数。

甚至说使用以下数据：

4 7
2 3 -2
3 2 -2
3 4 3
2 4 4
1 3 3
1 4 10
1 2 3

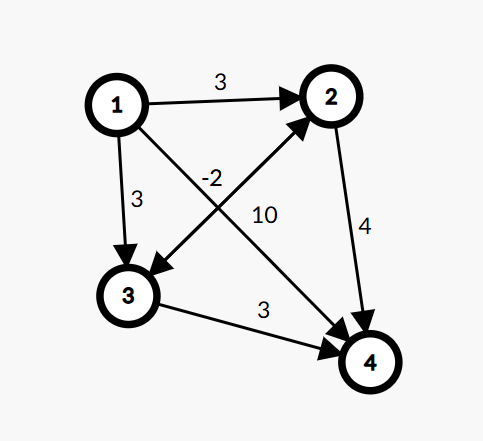
可以输出 0 3 3 5 这种数据，松弛次数甚至超过了 \(n\)（无负环），更可以说明不成立。
如图：