实验 4 函数和数组的应用编程

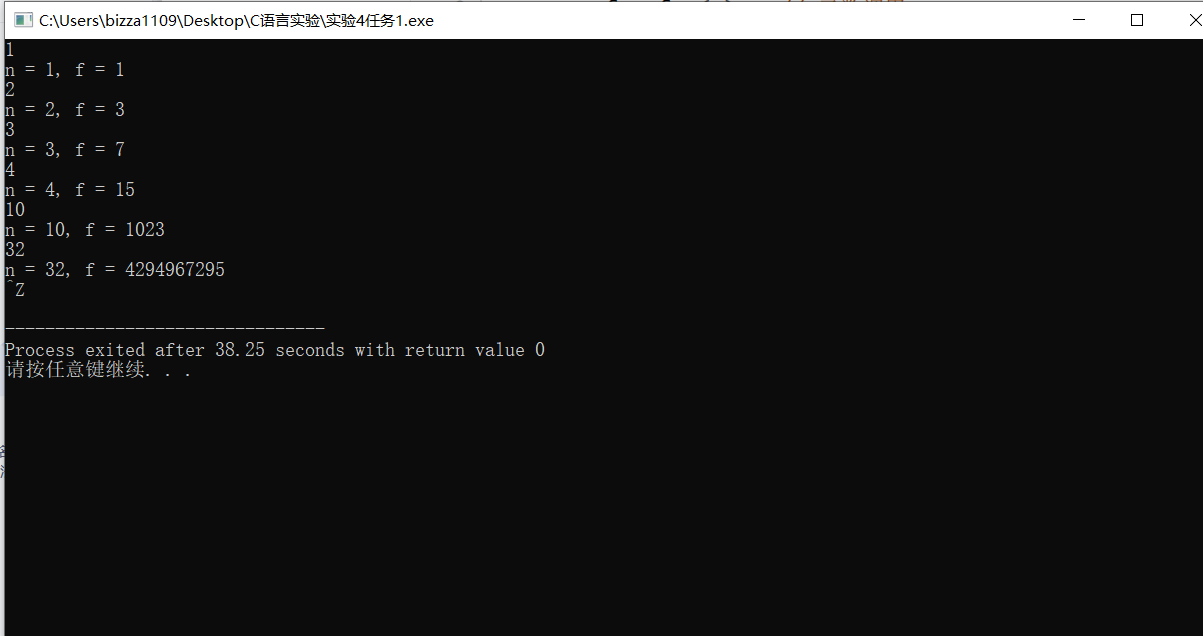
#include <stdio.h> 
long long fun(int n);
int main() 
{ 
    int n; 
    long long f; 
    while(scanf("%d", &n) != EOF) 
    { 
        f = fun(n); 
        printf("n = %d, f = %lld\n", n, f); 
    }
    return 0;
}

long long fun(int n)
{
    if(n == 1)
        return 1;
    else
        return 2*fun(n-1)+ 1;
}

 

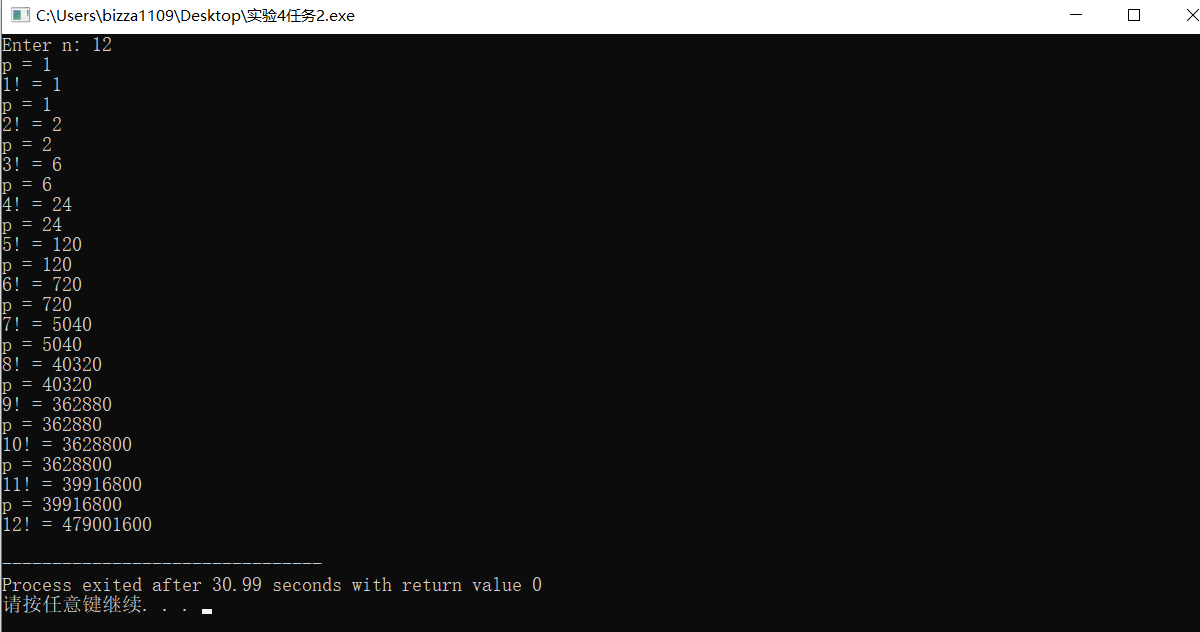
#include <stdio.h>
int main()
{
    int n;
    int a[1000]; //开一个足够大的数组。
    while(scanf("%d",&n)!=EOF)//输入想要输出n的多少次方，直到输入CTRL+Z为止。 
    {
        printf("n = %d 时,f=",n);
        for(int i=0;i<n;i++)
        a[i]=0; //先把数组每位数初始化为0。
        a[0]=1;//再让最后一位等于0，否则所有值都将为0。
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<n;j++)
                a[j]*=2; //每次循环数组中的每一位数都要乘以2。
            for(int j=0;j<n;j++)
            {
                if(a[j]>9)
                {
                    a[j+1]++; //如果数组中的一位数超过了9，需要进行进位操作。
                    a[j]=a[j]%10; //进位后自身取余。
                }
            }
        }
        for(int p=n-1;p>=0;p--) //由于在数组中存数时是从最后一位开始存的，所以要逆序输出。
        {
            if(a[p]>0) //数组中可能有很多位值为0，需要找出第一个不是0的位置输出。
            {    
                a[0]=a[0]-1;//所求为2^n-1，在最后一位减去1。
                for(int q=p;q>=0;q--)
                    printf("%d",a[q]);
                break;
            }
        }
        if(n==0) printf("0"); //特殊情况
        printf("\n");
    }
    return 0;
}

算法思路就是通过建立一个大的数组来存放计算结果，先计算2^n，从1开始每次×2，获得的数值一对一的放入数组中（从后往前），并且在这过程中要考虑到进位运算，并且要保留进位过后的余数。由于存放时从后向前，所以需
要进行逆序输出，在此过程中，因数组定义时较大，可能存在很多0，所以需要从第一个非0数开始输出，最后在计算完2^n的基础上减去1得到结果并输出。

 

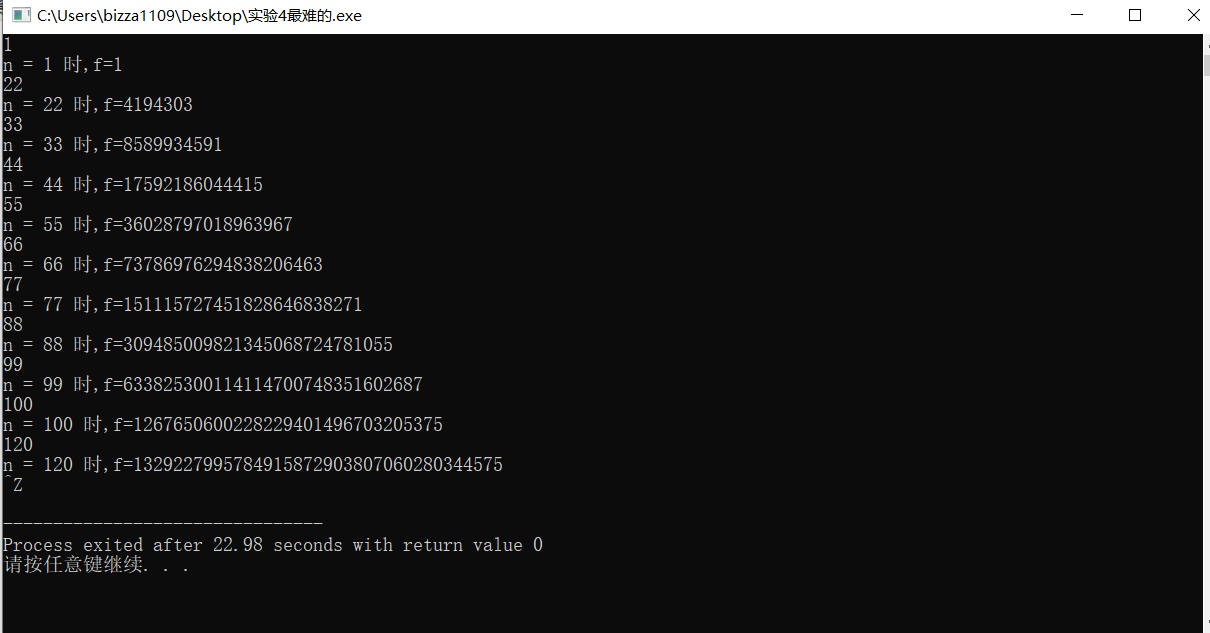
#include <stdio.h>
long long fac(int n);

int main() {
    int i,n;
    
    printf("Enter n: ");
    scanf("%d", &n);
    
    for(i=1; i<=n; ++i) 
        printf("%d! = %lld\n", i, fac(i)); 
    
    return 0;
}

long long fac(int n) {
    static long long p = 1;
    printf("p = %lld\n",p);
    p = p*n;
    
    return p;
}

 

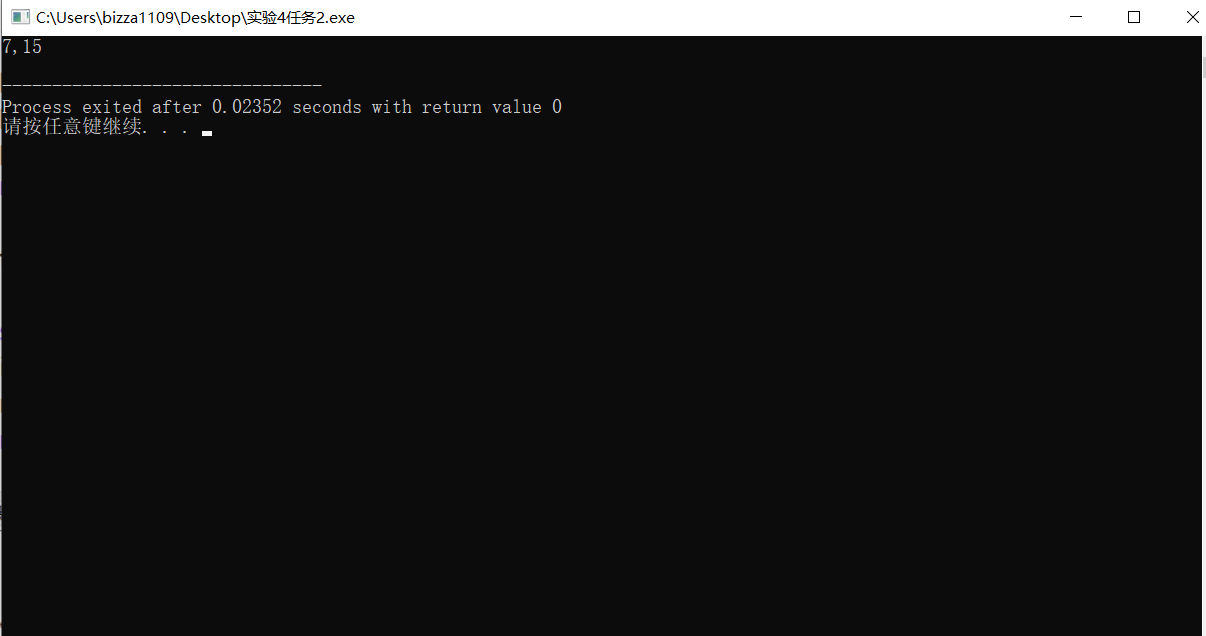
#include<stdio.h>
int func(int,int);
int main()
{
    int k = 4,m =.1,p1,p2;
    p1 = func(k,m);
    p2 = func(k,m);
    printf("%d,%d\n",p1,p2);
    return 0;
}
int func(int a,int b)
{
    static int m = 0,i = 2;
    i += m + 1;
    m = i + a + b;
    return (m);
}

 程序运行结果与理论分析结果一致。static修饰的局部变量特性是当函数退出时，变量始终存在，但不能被其他函数使用，并且再次进入该函数时，将保存上次的结果。

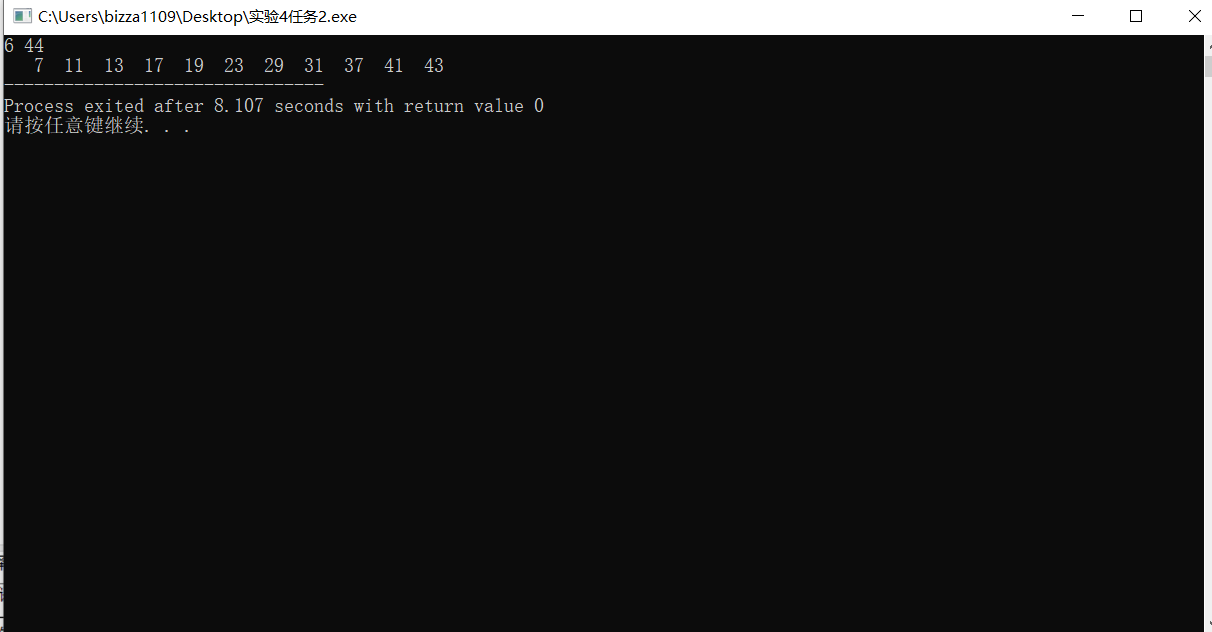
#include <stdio.h>
#include <stdlib.h> 
#define N 1000
int fun(int n,int m,int bb[N]) 
{
    int i,j,k=0,flag;
    
       for(j=n;j<=m;j++) 
    {
        flag=j;   
        for(i=2;i<j;i++)
            if(flag%i==0)
            {  
                flag=0;
                break;
            }
        if(flag!=0) 
            bb[k++]=j;
    }
    return k;
}

int main()
{
    int n=0,m=0,i,k,bb[N];
    
    scanf("%d",&n);
    scanf("%d",&m);

    for(i=0;i<m-n;i++)
    bb[i]=0;
        
    k=fun(n,m,bb); 
    
    for(i=0;i<k;i++)
        printf("%4d",bb[i]);
        
    return 0;
}

 

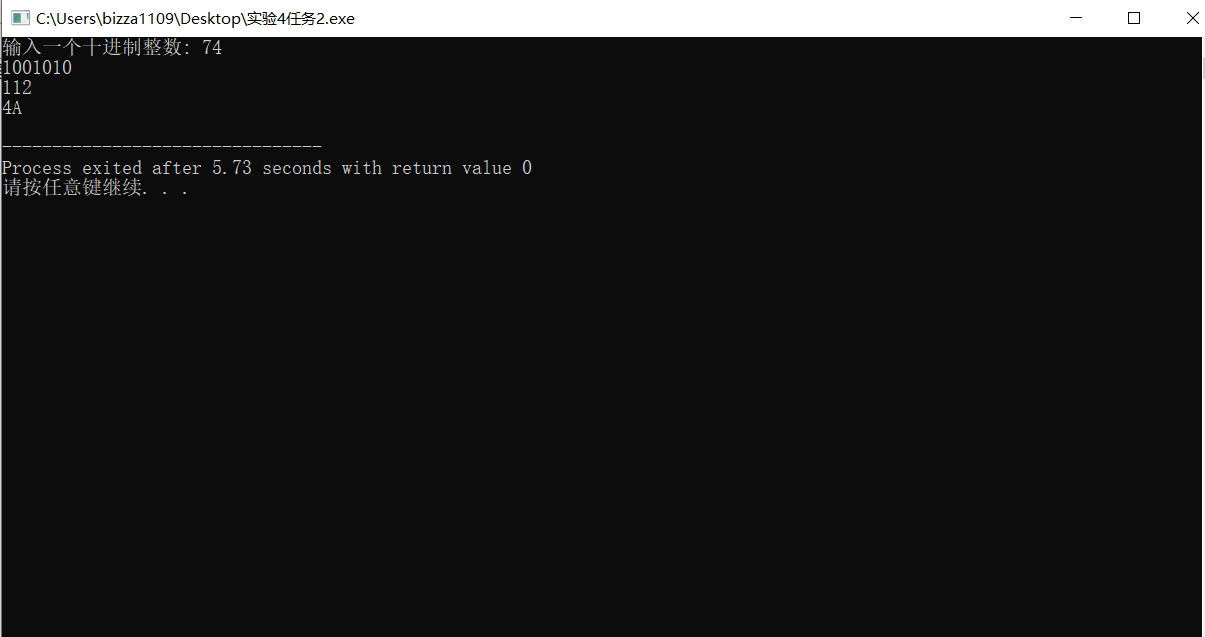
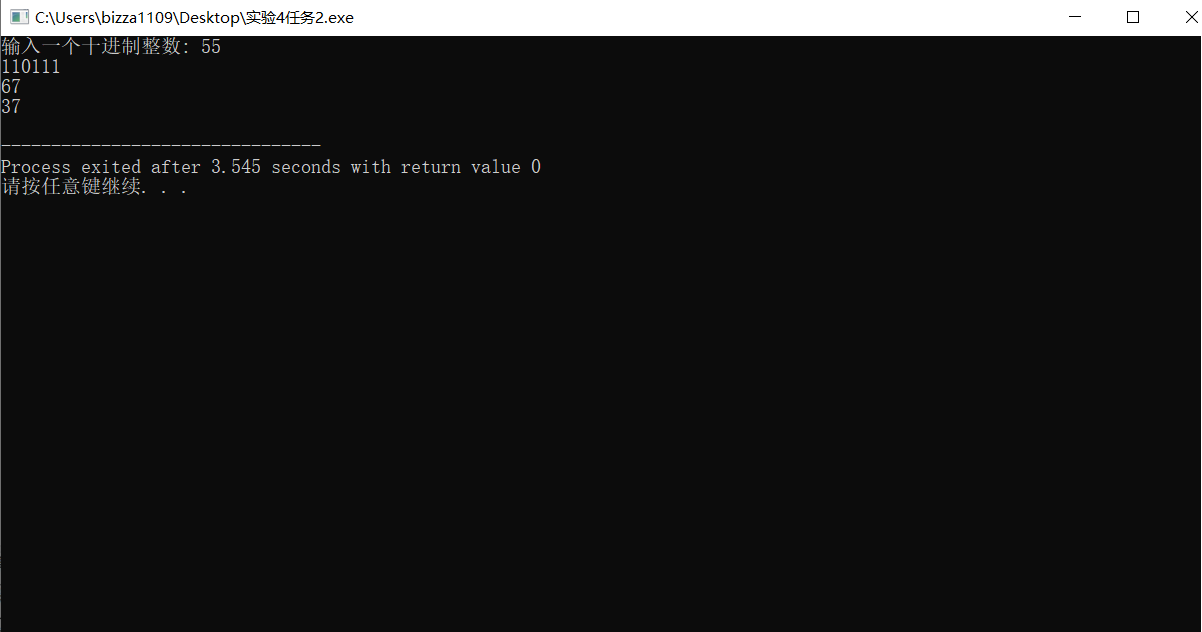
#include <stdio.h>
void dec2n(int x, int n); 

int main() 
{
    int x;
 
    printf("输入一个十进制整数: ");
    scanf("%d", &x);
 
    dec2n(x, 2); 
    dec2n(x, 8);
    dec2n(x, 16);
 
    return 0;
}
void dec2n(int x, int n) 
{
    int i,j,a,c;
    char b[100];
    a = x;
    c = x;
    for(i=1;x;i++)
        x /= n;
    for(j=1;j<i;j++)
    {   
        c = (a % n);
        a /= n;
        b[j] = c;
    }
    if(b[j]>9)
    switch(b[j])
    {
        case 10:b[j]='A';break;
        case 11:b[j]='B';break;
        case 12:b[j]='C';break;
        case 13:b[j]='D';break;
        case 14:b[j]='E';break;
        case 15:b[j]='F';break;
    }
    for(x=i-1;x>0;x--)
        printf("%X",b[x]);
    printf("\n");
}