基于几何模型的跟踪方法——Pure Persuit算法

路径跟踪算法--Pure Persuit实现

1.算法简介

Pure Persuit是一种基于几何的路径跟踪算法，又叫作纯跟踪算法。该算法最早由R. Wallace在1895年提出。该方法的核心是基于当前车辆的后轮中心位置(车辆质心)，在参考路径上设置前视距离\(l_d\)，根据\(l_d\)的距离匹配一个预瞄点，然后车辆通过计算角速度移动到该预瞄点。

2.核心思想

• 几何跟踪：通过简单的几何关系实现路径跟踪，无需复杂的动力学模型
• 前视距离：通过设置前视距离\(l_d\),以车后轮中心为基点，通过控制前轮转向，使得车辆沿着预设圆弧移动到前视点。
• 曲率控制：根据\(l_d\)的距离，基于三角形正弦定理，计算转向半径，生成方向盘转角

3.原理推导

假设车辆后轮中心能够按照一定的转弯半径R行使到该预瞄点，然后根据前视距离\(l_d\)、转弯半径R、车辆坐标系下的朝向角\(\alpha\)之间的几何关系来计算前轮转角\(\delta\)

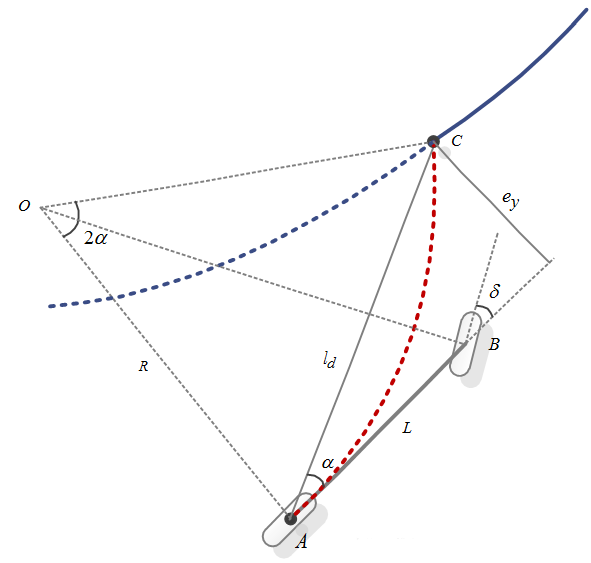
其中：

• R: 转弯半径
• \(l_d\): 前视距离
• \(\alpha\): 前视点和车辆当前位置倾角
• \(\delta\): 前轮转角

如上图，三角形OAC根据正弦定理有

\[\frac{l_d}{sin(2\alpha)}=\frac{R}{sin(\frac{\pi}{2}-\alpha)} \]

化简得

\[R=\frac{l_d}{2sin\alpha} \]

根据车辆的运动学方程有：

\[\delta=tan^{-1}\frac{L}{R} \]

所以我们可以计算得到前轮倾角:

\[\delta=tan^{-1}\frac{2Lsin(\alpha)}{l_d} \]

定义横向误差为后轮中心位置与预瞄点再横向的误差，如上图中的\(e_y\)

\[e_y=l_dsin(\alpha) \]

当前轮转角很小时，横向误差可以近似为

\[e_y=l_dsin(\alpha) \approx \frac{{l_d}^2\delta}{2L} \Rightarrow \delta=\frac{2Le_y}{{l_d}^2} \]

所以，该算法近似于一个P控制器，跟踪效果由前视距离决定。算法的本质就是对前视横向误差 \(e_{l_d}以\frac{2 L}{l_d^2}\)为比例系数的比例控制器。这样就建立起了转向角\(\delta\)和前视距离\(l_d\)，还有车辆轴距L以及目标点方向和当前航向角夹角\(\alpha\)之间的关系。

4.算法实现步骤

• 1.确定车辆的当前位置。
• 2.找到规划路径中离车辆最近的路径点。
• 3.确定前视距离\(l_d\)：由人为给定，通常认为和速度相关，车速很快的时候，就需要尽可能的看得远些；反之，车速比较慢时，需要看得比较近些。一种最常用的方法就是把前视距离表示为车辆纵向速度的线性函数，即：\(l_d=k \cdot v+l_0\),其中k为速度增益值，\(l_0\)是一个基础前视距离（或称为静态前视距离）。
• 4.找到目标点𝐺：以车的后轮中心为圆心，\(l_d\)为半径画圆弧，在规划路径上找到距离车辆后轮中心\(l_d\)距离的交点，交点在不同路径中可能不只一个，通常情况下选择比较靠近车辆的目标点为最终的预瞄点。
• 5.将目标点转换为车辆坐标系下，方便计算横向误差。
• 6.根据公式计算转角，并要求车辆将转向设置为该转角