线性代数笔记20——行列式和代数余子式
行列式
如果有两个向量<a1, a2>和<b1, b2>,那么这两个向量组成的行列式是:
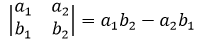
看起来只是表示一个简单的计算,仅仅计算了一个数值,但是别忘了,行列式是由向量组成的,它一定会表示向量间的某种关系。
在《线性代数笔记4——向量3(叉积)》中我们看到,二阶行列式表示了二维平面中以两个向量为临边的平行四边形的面积;三阶行列式表示在三维空间中以三个向量为临边的平行六面体的体积;推广到n维空间,n阶行列式表示在n维空间中图形的n维体积。实际上我们无法有效表示出三维以上的空间。对于物理世界中更多维的空间,绝大多数人都无法想象,但是数学却可以给出明确的定义。
对于n维空间的行列式,可以表示为:
Dn = |An×n|
其中A是一个n×n的矩阵。
行列式是由向量引出的,解释的也是向量的性质,在看到行列式时一定要在头脑中映射出向量,实际上线性代数的本质就是对向量的研究。
行列式的性质
性质0,单位矩阵的行列式为1
这个不解释。
性质1,如果Dn= |A|中某行的元素全为0,那么Dn = 0
这个性质较为明显,在多维空间中,行列式表示的是体积,如果其中一个维度的模为0,那么体积也是0。
性质2,如果Dn= |A|中某两行元素对应成比例,那么Dn = 0
很多时候我们都喜欢用实例推导性质,像下边这样:
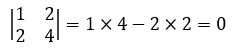
或者用代数形式:
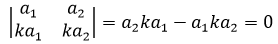
但是性质应当由定义推导,然后用计算去验证,而不是用计算去推导。现在我们尝试用行列式的定义去推导。行列式表示的是向量间的关系,以二维空间为例,如果某两行元素对应成比例,那么说明一种一个向量是另一个向量的延伸,它们的夹角是0°或180°,即二者平行,两个平行的向量围成的面积是0:

性质3,如果Dn= |A|中某两行元素互换,那么互换后的行列式变号,即|A|= -|A|
两个向量的模长是a和b,与x轴的夹角分别是α和β,如下图所示:

平行四边形的面积:

如果两个向量互换:
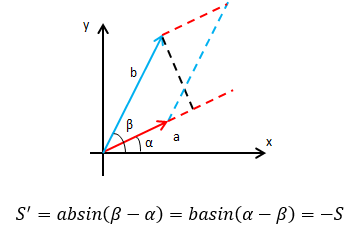
在代数学中,角度、面积、体积可以是负的。用计算去验证:
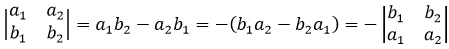
性质4,倍乘性质
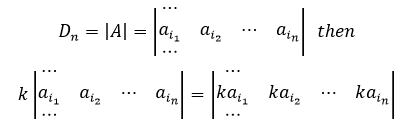
实际上是将外部的k乘到其中的一行,把平行四边形的一条边扩大k倍,则面积也扩大了k倍,如下图所示:

需要注意的是行列式与矩阵的区别,矩阵扩大k倍是将矩阵中的全部元素都乘以k(矩阵中的每个元素都对应了一个向量的分量,这在下文关于矩阵的介绍中会有所说明),这将有下面的关系:
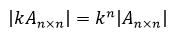
性质5,倍加性质
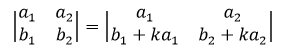
对于更高阶的行列式也一样。下图平行四边形的斜边展示了一个向量加上另一个向量的k倍:
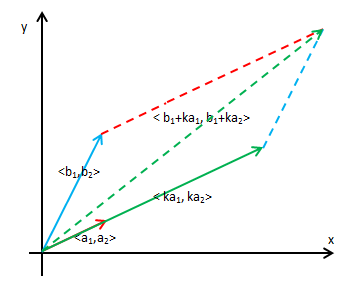
两个平行四边形的面积是相同的,所以倍加公式成立。
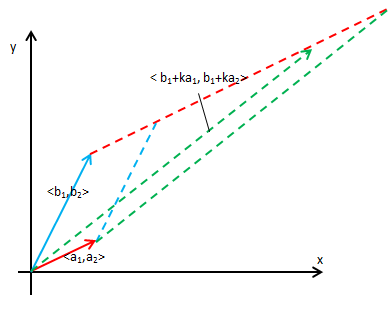
性质6,单行可拆(加)性
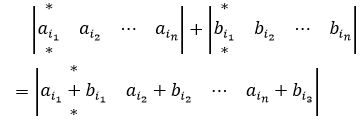
其中*号表元素完全相同,从左到右叫加,从右到左叫拆。以二阶行列式为例:
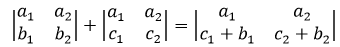
为了简单,将<b1,b2>和<a1,a2>分别设置在两个坐标轴上,如下图示:
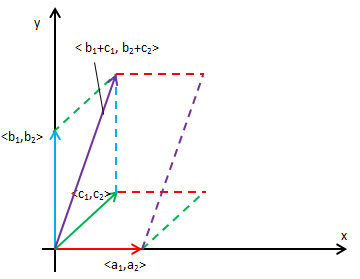
<a1,a2><b1,b2>所围平行四边形面积是a2 b2,<a1,a2><c1,c2>所围平行四边形面积是a2 c2,<a1,a2>< b1+c1, b2+c2>所围平行四边形面积是a2(b2+c2),由此可见性质6成立。
性质7,以上所有作用于行的性质也可以作用于列上,即|A| = |AT|
性质8,两个矩阵相乘的行列式,等于这个两个矩阵的行列式相乘,|AB| = |A||B|
当两个矩阵相等时,矩阵平方的行列式等于矩阵行列式的平方:
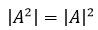
可以借助性质8计算A-1的行列式:
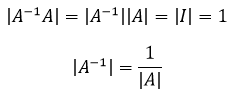
如果1/|A|有意义,则|A| ≠ 0,A有逆矩阵;反之,如果|A| = 0,A是奇异矩阵。这就是性质9。
性质9,如果|A| = 0,A是奇异矩阵。
行列式的意义
行列式是由向量组成的,当Dn = |A| ≠ 0 时,意味着组成|A|的向量全部独立。所谓独立,就是向量围成的n维空间中图形的n维体积不为0。这似乎没有太大价值,但是如果把行列式转换为方程组就意义重大了,以二阶行列式为例:
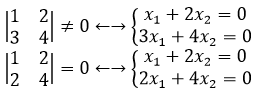
可以看到,对于全部独立的向量,方程组有唯一解,否则方程组无解或有无数解。当|A| ≠ 0时,说明至少有一个向量是“多余”的,正是这个多余的向量使得n维体积为0。以阶行列式为例,当体积为0时,说明三个向量在同一平面内,这意味着,一定可以通过倍乘和倍加性质用另外两个向量表示第三个向量,从而完全消除第三个向量。N元一次方程组需要N个完全不同的等式,现在少了一个等式,所以无法得到唯一解。
线性代数研究的是向量之间的关系,向量间最重要的关系就是独立或不独立,行列式是否等于0正是这种关系的有效描述。
行列式的计算
上三角矩阵的行列式等于主对角元素的乘积:
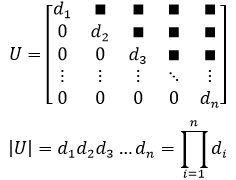
对于更多阶的行列式,一种有效的计算方法是先将其消元,转换为上三角行列式,然后在计算这个上三角行列式的值。以二阶行列式为例,我们已经知道它的结果:
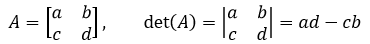
利用消元法将A转换为上三角矩阵:
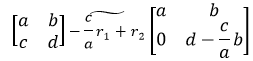
现在可以直接利用主对角线的元素相乘:
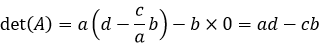
行列式的公式
行列式的性质也可以用于计算行列式的值,以二阶行列式为例:
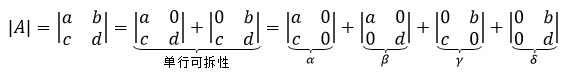
在反复利用行列式的单行可拆性后,A分解成4项,每一行只有一个非零元素。二阶行列式计计算的是图形的面积,对于α来说,由于构成行列式的两个向量<a, 0>和<c, 0>是在同一个维度上的直线,所以二者围成的面积是0;同理,δ也一样。
Β是上三角矩阵,它的值是主对角线的乘积ad。γ可以使用行列式的行互换性质形成一个新的上三角矩阵:
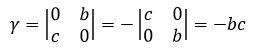
最终可以得到|A|的值:
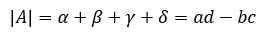
这种方法对于更高阶的行列式也同样适用,三阶行列式按照每一行只有一个非零元素的原则全部展开后将长达33项,这将占用长长的篇幅,可以考虑一个能够缩减展开式的办法。根据行列式的几何意义,行列式计算的是n维图形在n维空间中的n维体积,3阶行列式计算的自然是三维空间的体积,如此一来,只有三个向量分别指向三个不同维度时,才能保证体积不等于0,因此三阶行列式可以展开成:

现在只剩下3! = 6项,每一项都可以通过行列式的行交换性质变成上三角行列式(或者本身就是上三角行列式),这样就可以得到行列式的最终值:
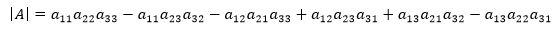
现在可以归纳出n阶行列式的公式:
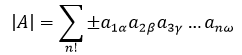
下标的数字项表示行号,希腊字母表示列号(实际数量可能远超过希腊字母的数量,暂且用希腊字母代替)。这相当于是列号的排列,在每一项中,n个列标都各用一次。负号的目的是为了应对行交换的情况。
根据公式,对于n阶单位矩阵来说,只有主对角线的一项不是0,所以单位矩阵的行列式的值是1。
示例 计算A的行列式:

通过消元法计算是正确的选择,通常也应该这么做,实际上不难看出这个A是一个奇异矩阵,所以它的行列式等于0,现在用行列式的公式来验证这个结论。根据公式, |A|的大多数展开项都等0,没有被淘汰的只有两项,二者相加等于0:
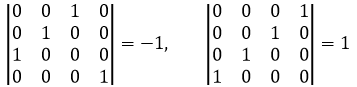
第一个行列式是负值,因为它需要用1、3行进行一次行交换来变成上三角矩阵:
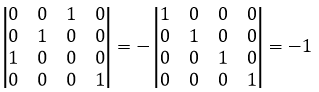
代数余子式
代数余子式是从行列式的公式中提取出来的,它的作用是把n阶行列式化简为n – 1阶行列式。我们以三阶行列式为例,看看代数余子式是什么。根据行列式的公式,3阶行列式展开,将得到:
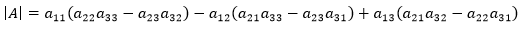
这实际上式选定第一行的一列,然后考虑各种可能的排列,为了突出重点,写成下面这样:
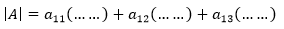
注:根据第任何一行展开都将得到同样的结果,下面是根据第二行展开:
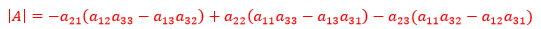
按列展开也可以,比如按第一列展开:
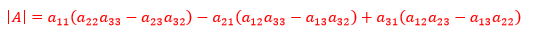
括号中由剩余因子组成的表达式就是代数余子式(第二项把符号移到了括号中,下节会说明原因),比如a22a23 – a23a32是a11的代数余子式。可以用更直观的方式表达a11(a22a23 – a23a32):

代数余子式的符号
-a12(a22a23 – a23a32)可以表示成:

注意到上式有一个负号,我们一般不需要 -a12的代数余子式,所以a12的代数余子式需要把符号移到括号中:
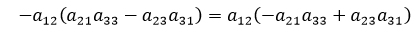
代数余子式本身就是行列式,只是它的正负号需要单独判断,判断方法是根据选定元素行号和列号之和的奇偶性。用Cij表示aij的代数余子式,当i + j是偶数时,行列式取正号,是奇数则取符号。比如三阶行列式中,C12的行列号之和是3,它对应的代数余子式取符号。如果有一个五阶行列式,它的每一项的代数余子式的符号是这样分布的:
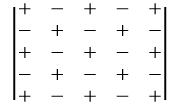
行列式的代数余子式展开
把某个行列式的用代数余子式展开实际上也是求行列式的另一种方法,可以表示成:
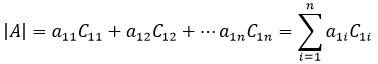
代数余子式本身是n - 1阶行列式,它可以继续展开成n - 2阶行列式……如此展开下去,直到1阶行列式为止,其核心思想是把一个复杂的高阶行列式转换成多个简单的低阶行列式。
由于行列式根据任何一行展开都可以,所以:
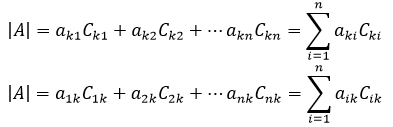
二阶行列式的代数余子式
用代数余子式可以解释二阶行列式的计算公式。二阶行列式可以用一阶代数余子式展开:
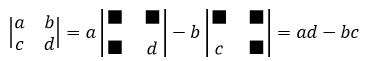
由于b是第1行第2列,1 + 2 = 3是奇数,所以b对应的代数余子式C12是以符号开头的。
作者:我是8位的





 浙公网安备 33010602011771号
浙公网安备 33010602011771号