概率统计20——估计量的评选标准
对总体参数进行估计的方式多种多样,为了评判估计量的优劣,我们需要借助一些评选标准。
这些乱七八糟的符号
我觉得参数估计总是人为地设计各种门坎,里面参杂着各种符号,一会儿是X,一会儿是x;一会儿是θ,一会儿是θ(X);还有诸如“总体参数”、“待估计参数”这类名词,究竟是几个意思?
有必要先理清这些符号。
我们用全国18~50岁的男性身高为例,所有18~50岁的男性是总体。在概率统计中,当我们说到总体,就是指一个具有特定概率分布的随机变量,这个随机变量用X表示,X符合某某分布。n表示总体的数量,假设这些男性有3亿,那么n就等于3亿。在做统计的时候肯定不能普查所有人,这样成本也太高了,因此才有抽样。当然抽样也有多种形式,比如均匀抽样、拒绝抽样等,这是另外的话题,在数据分析专栏中将陆续展开。
现在调查了100万个符合条件的男性,这些男性就构成了“整体中的一个样本”,用X1, X2, …, Xm表示,Xi表示样本中的第i个男性,m是样本的容量,m等于100万。样本中的每个男性都有特定的身高,是一个具体的数值,这个值用小写的x表示,x10 = 176cm表示样本中的第10个数据的值是176cm,此时X10 = x10。这有点类似于P(X=x)的意思,X表示随机变量本身,x表示某个特定的数值。
值得注意的是,如果用X1, X2, …, Xm表示样本,则强调样本是随机的,是理论上的、尚未诞生的样本,样本中的每个数据都是一个随机变量;如果用x1, x2, …, xm表示样本,则强调样本中的随机变量已经有了特定的取值,是已经拥有的样本。
此外,n的值不一定很大,如果调查某个特定班级的平均身高,那么n的值就只是这个班级的学生数,比如n=60。n也不一定是个确定的值,比如从建国到现在全国人民一共消费了多少斤啤酒,没有具体的数,只知道这个数大到没边。
现在我们知道18~50岁的男性身高符合某个均值为μ,方差为σ2的正态分布X~N(μ, σ2),μ和σ2称为“总体的参数”,正是这两个值决定了分布的具体形态,用大Θ表示总体参数的集合。总体参数不止一个,这里的μ和σ2都是总体的参数。θ是总体中的某一个参数,它可以代表μ,也可以代表σ2,有点变量的意思,可能用x比用θ更好理解,但是x已经被占用了。此外,用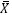 表示样本的均值,用S2表示样本的方差。
表示样本的均值,用S2表示样本的方差。
现在θ的具体值是多少不知道,需要根据样本X1, X2, …, Xm估计总体参数θ,具体估计量用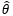 表示。
表示。 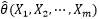 表示
表示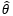 是由具体的样本X1, X2, …, Xm估计出来的,
是由具体的样本X1, X2, …, Xm估计出来的, 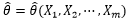 仅仅是为了强调这一点,至于怎么估计是另一回事。这也有点类似于y = y(x),第一个y是个具体的数值,这个数值是由x决定的,第二个y是一个映射关系,至于是什么映射关系是另一回事。有时候也把m个样本记作X = {X1, X2, …, Xm},因此有了
仅仅是为了强调这一点,至于怎么估计是另一回事。这也有点类似于y = y(x),第一个y是个具体的数值,这个数值是由x决定的,第二个y是一个映射关系,至于是什么映射关系是另一回事。有时候也把m个样本记作X = {X1, X2, …, Xm},因此有了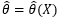 ,如果用θ表示μ,就有了
,如果用θ表示μ,就有了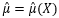 。这里的X不再是总体,而是来自于总体中的样本,至于X到底是总体还是样本,需要根据上下文确定。
。这里的X不再是总体,而是来自于总体中的样本,至于X到底是总体还是样本,需要根据上下文确定。
多个参数产生的问题
已知总体的均值是μ,方差是σ2>0,但是不知道二者的具体数值,作为补偿,我们拥有总体中m个数据样本,X1, X2, ……,Xm。现在想要通过这些样本估计总体的概率分布模型,即通过样本估计μ和σ2的具体数值。
已知总体有期望和方差两个数字特征,但不知道具体值,这比直接说啥也不知道强不了多少。
假设我们已经使用直方图之类的工具分析过样本,或直接咨询过领域内的相关专家,得知总体应当符合正态分布,X~N(μ, σ2)。现在我们可以用多种方法估计μ和σ2?
点估计和连续性修正(概率统计17)中的介绍,样本矩的估计量是:

一维正态分布的最大似然估计(概率11)中,最大似然估计也能得到类似的结论:
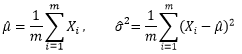
当m很大时,1/m和1/(m-1)的差距也很小,可以认为矩估计和最大似然估计的结论相等。我们能否因此得出一个结论,说两种估计法在任何分布下得到的结论都相同?
还是估计总体的均值和方差,这次从样本的分析中得知,总体可能符合X~[a, b]的均匀分布。
在再看大数定律(概率统计18).中我们已经知道均匀分布的密度函数,从而求得均匀分布的均值和方差:
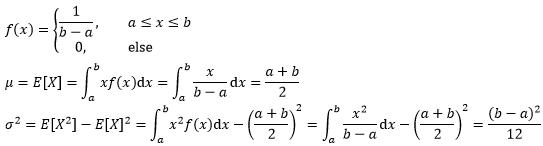
使用矩估计求得样本的均值和方差时,我们将认为样本矩等于总体矩,从而得到一个关于a和b的方程组,进而求得a和b的矩估计量:

这里也可以看出,矩估计的优点就是简单,不管总体服从什么分布,样本矩的计算方法都一样。
现在来看均匀分布下样本的最大似然估计。
用xmin和xmax表示样本值中最小的和最大的,对于X~[a, b]来说,所有样本的取值都在a,b之间,即xmin ≥ a,xmax ≤ b,似然函数是:
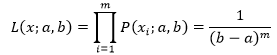
之后的目标是根据样本找到L(x;a,b)最大时a,b的取值:
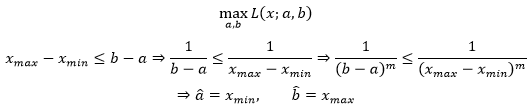
这个结果和矩估计明显不同。
现在的问题是,我们分不出这两个估计量的优劣。这就是我们要面对的新问题。
我们用 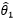 和
和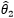 表示两种方案的估计量。对于不同的估计量,与真实值的差误差也不同,无法仅凭一个数值来评估估计量,而是使用一条曲线:
表示两种方案的估计量。对于不同的估计量,与真实值的差误差也不同,无法仅凭一个数值来评估估计量,而是使用一条曲线:
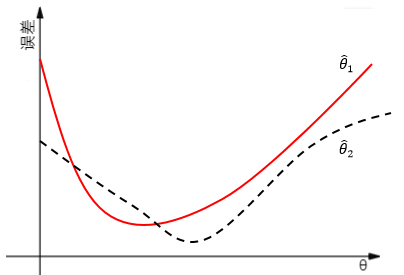
对于某些估计而言 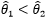 ,对于另外一些则可能相反。这就好比两个人的考试成绩,甲的语文成绩比较好,而乙的数学成绩更优秀。能否找出一个全优的学生呢?也就是对于整体中的全部参数,我们都希望估得最佳结果,以使得根据样本估计的分布接近整体分布。这是个美好的愿望,随着待估计参数的增加,找到全优学生的难度也急剧增大。因此为了找出最优估计量,我们必须添加一些额外的评判规则。这就涉及到如何评估估计量的问题。较为常用的三个标准是无偏性、有效性和相合性。
,对于另外一些则可能相反。这就好比两个人的考试成绩,甲的语文成绩比较好,而乙的数学成绩更优秀。能否找出一个全优的学生呢?也就是对于整体中的全部参数,我们都希望估得最佳结果,以使得根据样本估计的分布接近整体分布。这是个美好的愿望,随着待估计参数的增加,找到全优学生的难度也急剧增大。因此为了找出最优估计量,我们必须添加一些额外的评判规则。这就涉及到如何评估估计量的问题。较为常用的三个标准是无偏性、有效性和相合性。
无偏性
X1, X2, …, Xm是来自于总体中的样本,θ是总体分布的参数,θ∈Θ,根据样本可以得到θ的估计量:

如果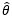 的数学期望存在,且:
的数学期望存在,且:
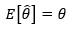
如果对于整体中的任意θ,上式都成立,则称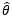 是θ的无偏估计量。
是θ的无偏估计量。
这到底是啥意思?参数为什么能有期望?
无偏性的数学解释
首先需要回顾第一节的内容,清楚地了解这些符号的真正含义。
设总体X的均值为μ,方差是σ2>0,它们都是整体分布的参数,且都是待估计的未知参数。既然μ和σ2都是和总体分布有关的参数,它们自然都可以用θ表示,作为估计量的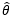 也就代表了
也就代表了 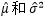 。在这个例子中,“
。在这个例子中,“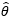 是θ的无偏估计”意味着:
是θ的无偏估计”意味着:
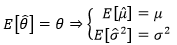
如果使用矩估计,则根据再看大数定律(概率统计18)中的内容,样本均值的期望与方差是:

这表明样本均值是整体均值的无偏估计。
样本的方差是:

这里之所以用Xi而不是xi,是为了强调样本的随机性,可以简单地理解为计划抽取一个随机样本,但还没有真正开始抽取。
现在看看E[S2]是多少。
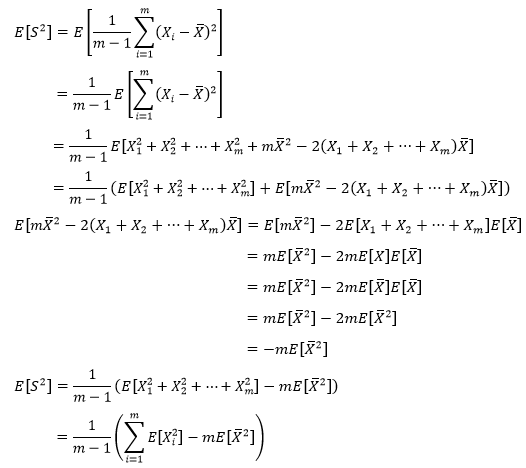
根据方差的性质:
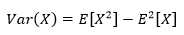
对于样本中的任意一个随机变量来说,方差和期望都相等:
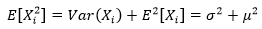
此外:
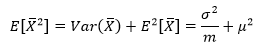
最终:
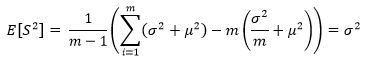
上面的结论表明,样本方差S2也是总体方差的无偏估计,这也附带说明了样本方差的系数是1/(m-1)的原因,如果取1/m,则估计量无法确保无偏性。
从这个例子中也看出,无论总体符合什么分布,样本均值都是整体均值的无偏估计,样本方差也都是总体方差的无偏估计。
无偏性的意义
样本X1, X2, …, Xm是随机的,因此根据这些样本得出的估计量 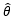 也是随机的,我们已经多次重申过这一点。既然
也是随机的,我们已经多次重申过这一点。既然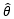 是随机的,那么一个自然的结论是:根据样本的不同,有些估计量可能偏大,有些可能偏小。反复将这一估计量使用多次,就“平均”来说其偏差为零。
是随机的,那么一个自然的结论是:根据样本的不同,有些估计量可能偏大,有些可能偏小。反复将这一估计量使用多次,就“平均”来说其偏差为零。
在科学技术中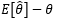 称为以
称为以 作为θ估计的系统误差。无偏估计的实际意义就是无系统误差。
作为θ估计的系统误差。无偏估计的实际意义就是无系统误差。
既然如此,是否意味着无偏估计一定好呢?通常来讲是的,但也不尽然,比如下图中,有偏的甲明显更优于无偏的乙。
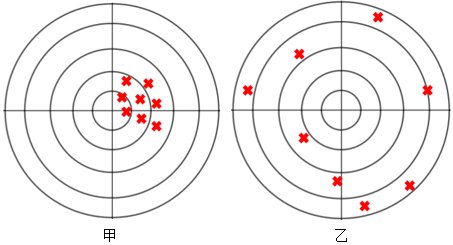
不同的无偏估计量
设总体X服从指数分布,概率密度为:
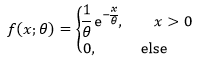
其中参数θ未知,X1, X2, …, Xm是来自X的样本,根据指数分布的性质:
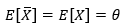
因此样本均值是参数θ的无偏估计量。
然而估计量不止一种,下面的mZ也是θ的无偏估计量:

Z具有概率密度:

可见一个未知参数可能有不同的无偏估计量。
有效性
同一个参数为什么会出现不同的无偏估计量呢?我们可以想象一个场景:任何人都可以估计明天的天气,至于是否准确另当别论。同样是估计天气,气象局的天气预报显然更准确。但就无偏性来说,普通人和天气预报的平均偏差都为0。这就好比甲乙二人的射击比赛,甲的成绩明显高于乙,但无偏性却告诉我们二者的成绩相同,这显然是荒谬的:
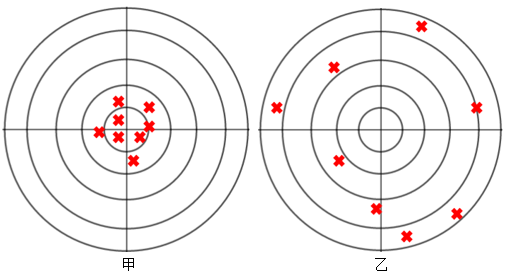
对于上图来说,谁的成绩越接近靶心,谁的成绩就越好,这也正是有效性的基本逻辑。对于参数θ的两个无偏估计量 ,谁和θ更靠近,谁就越好。一种自然的方式是比较不同的无偏估计量与θ之差的绝对值,但是绝对值不易处理,于是使用平方误差法,这也是一种常用的较为简便的方式。如果对于整体中的任意θ,都有:
,谁和θ更靠近,谁就越好。一种自然的方式是比较不同的无偏估计量与θ之差的绝对值,但是绝对值不易处理,于是使用平方误差法,这也是一种常用的较为简便的方式。如果对于整体中的任意θ,都有:
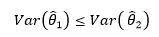
则称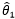 比
比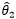 有效。
有效。
再次强调的是,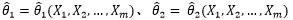 都是随机值,因此才通过期望来去掉随机性,进而比较二者谁更有效:
都是随机值,因此才通过期望来去掉随机性,进而比较二者谁更有效:
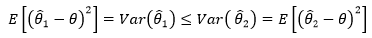
另一个值得关注的问题是,有效性还强调了对于任意θ∈Θ都成立。如果总体参数θ中包含两个待估计变量,只有当方案1的两个估计量全部优于方案2时,才能说方案1比方案2更有效。
对于上节的指数分布来说:
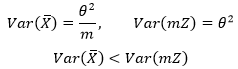
因此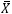 比mZ更有效。
比mZ更有效。
相合性
简单而言,如果当样本的容量增大时,估计量逐渐收敛于待估计参数的真实值,那么称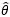 是θ的相合估计量。
是θ的相合估计量。
相合性是对一个估计量的基本要求,如果估计量不具有相合性,那么无论样本的容量有多大,都无法将参数估计得足够准确,这种估计已经有点近似于胡乱猜测。
优化的策略
有了评选标准之后,我们就可以使用一些优化策略,找出最优估计量。
无偏性为估计量加上了限制,有了这条限制,大多数不太好的估计量会被排除。经过无偏性的筛选后,再使用有效性求得的最优解称为最小方差无偏估计量(uniformly minimum variance unbiased estimate,UMVUE)。
尽管我们可以通过减少候选项的方式找出最优解,但需要认清的事实是,找到任何情况下都适用的全能最优解绝非易事。既然如此,不妨改变策略,弱化最优解的定义,只要满足相合性和渐进有效性,就认为这个解是可以接受的。
渐进有效性:当样本容量n→∞时, 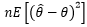 收敛于理论边界。
收敛于理论边界。
最大似然估计就是这种策略下最常用的方案。
在最小方差无偏估计中,我们实际上是想找到总分最优的估计量,但这种方法假设所有参数都是平等的,并没有为参数分配恰当的权重。贝叶斯估计采用了另一种思路应对这个问题。
无论最小方差无偏估计还是最大似然估计,我们都认为待估计参数θ是个确定的值,比如1949年10月1日中华人民共和国成立,这是一个明确的日期。而在贝叶斯估计中,把θ也看作一个变量,所求的是θ的分布,也就是后验分布,如果后验分布较窄,则可信度较高,否则可信度较低。这类似于估计1949年10月1日中华人民共和国成立的概率是多少。贝叶斯估计的难点在于后验概率的计算较为复杂。关于更多先验和后验的问题将在后续章节陆续展开。
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”



 浙公网安备 33010602011771号
浙公网安备 33010602011771号