概率统计17——点估计和连续性修正
原文 | https://mp.weixin.qq.com/s/NV3ThVwhM5dTIDQAWITSQQ
概率(probabilty)和统计(statistics)是两个相近的概念,其实研究的问题刚好相反。
概率是使用一个已知参数的模型去预测这个模型所产生的结果,并研究结果的相关数字特征,比如期望、方差等。假设现在已知一个射击运动员的得分服从均值为8.2,方差为1.5的正态分布,就可以对这名运动员下一次射击的得分情况有个大致的预估。
统计与概率正好相反,是先有一堆数据,然后利用这些数据推测出模型和模型的参数。现在来了一名陌生的运动员,我们对他一无所知,不过他宣称自己是一名优秀的职业运动员。在进行了一系列射击测试后,教练组收集到了一批这名运动员的成绩,通过观察数据,认为他的成绩符合正态分布(也就是确定了模型),之后再进一步通过数据推测模型参数的具体值。对于正态分布来说,参数是均值和方差。
这样看来,我们碰到的大多数问题都是统计问题,虽然概率是随机事件的客观规律,但遗憾的是,这个规律总是作为未知量出现的,作为补偿,我们拥有一系列数据样本,虽然这些样本可能远小于整体,但仍然可以以点带面,根据这些样本对整体参数进行估计,得出关于整体概率分布的近似值。这个根据样本对总体参数进行估计的过程就是参数估计。根据参数性质不同,可分为点估计和区间估计。
点估计就是用样本统计量的某一具体数值直接推断未知的总体参数,得到的是一个具体的参数值。我们之前讲过的矩估计、最大似然估计、贝叶斯估计都是点估计。
我们以矩估计为例,重新看看怎样由样本估计总体。
总体数量和样本数量
我们经常用n表示总体的数量,究竟什么才算总体呢?
总体总是给人以“多”的概念,但事实并非如此,不同问题的“总体”数量可能相差很远。比如一个啤酒厂一年生产的罐装啤酒是1000万,一个班级的学生数是60人,无论是1000万还是60,都是总体。用n表示总体的数量。
既然是用样本估计总体,当然少不了抽样,关于抽样可参考:数据分析(4)——闲话抽样 | 看似公平的随机抽样是否真的公平?。 用m表示样本的数量。
估计总体的均值
医生的判断很大程度依赖于血液检测的结果。从抽血结束到取得报告单需要一段时间,这段时间并不确定,也许运气较好,十几分钟就拿到了,也可能等上一小时。现在得到了一组样本,X = {x1, x2, ……, xm},其中每个数据代表了一名患者取得报告单前的等待时间。我们的目标是根据这组样本对整体的平均等待时间做一个估计。
计算方式很简单,只需要计算样本的均值就可以了:
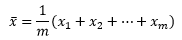
我们认为样本的分布与整体的分布相似,这个均值是根据目前已知的数据对总体的最佳近似描述。这种用样本均值估计总体均值的方法称为矩估计,估计的结果是总体均值的点估计量。
下面的代码展现了整体分布和抽样分布的关系:
import numpy as np import matplotlib.pyplot as plt from scipy import stats fig = plt.figure(figsize=(10, 5)) plt.subplots_adjust(hspace=0.5) # 调整子图之间的上下边距 mu, sigma_square = 30, 5 # 均值和方差 sigma = sigma_square ** 0.5 # 标准差 xs = np.arange(15, 45, 0.5) ys = stats.norm.pdf(xs, mu, sigma) ax = fig.add_subplot(2, 2, 1) ax.plot(xs, ys, label='密度曲线') ax.vlines(mu, 0, 0.2, linestyles='--', colors='r', label='均值') ax.legend(loc='upper right') ax.set_xlabel('X') ax.set_ylabel('pdf') ax.set_title('X~N($\mu$, $\sigma^2$), $\mu$={0}, $\sigma^2$={1}'.format(mu, sigma_square)) for i in [1, 2, 3]: m = 10 ** i # 样本数量 np.random.seed(m) X = stats.norm.rvs(loc=mu, scale=sigma, size=m) # 生成m个符合正态分布的随机变量 X = np.trunc(X) # 对数据取整 mu_x = X.mean() # 样本均值 ax = fig.add_subplot(2, 2, i + 1) ax.hist(X, bins=40) ax.set_xlabel('X') ax.set_ylabel('频度') ax.set_title('m={0},样本均值={1}'.format(m, mu_x)) plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 # plt.rcParams['axes.unicode_minus'] = False # 解决中文下的坐标轴负号显示问题 plt.show()
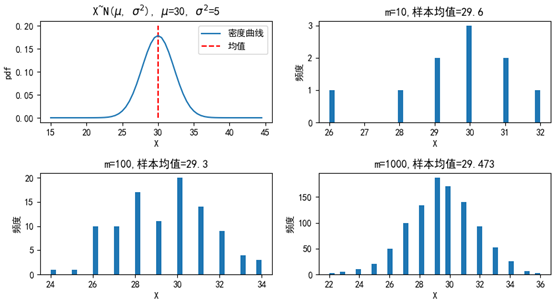
可以看到,抽取的样本越多,样本的分布越接近整体的分布。这里有问题的是均值的符号,在各种资料中一会是μ,一会是戴帽子的μ,一会是x拔,到底用哪个?

过去我们一直说某些问题符合X~N(μ, σ2)的分布,这里μ是总体均值;在最大似然估计中得出的结果用 表示,说明这是通过样本对整体均值的一个点估计量。
表示,说明这是通过样本对整体均值的一个点估计量。
估计总体的方差
假设我们已经预先计算出了均值的点估计量,是否可以像计算总体方差一样计算样本方差呢?
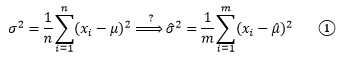
从上面的整体分布图可以看到,大部分数据集中在均值附近,极端值出现的概率很低,这意味着对于抽样来说,样本数越小,抽到极端数值的可能性就越小。方差刻画了数据相对于期望值的波动程度,由于样本的极端值出现的概率很低,因此样本的波动很可能低于总体的波动,方差较整体方差更小。为了应对这种情况,我们经常看到的是另一个计算样本方差的公式:
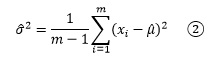
a/(m - 1)肯定大于a/m,这使得②的结果稍大于①,m的值越小,①和②的差别越明显。随着样本数量的增加,取得极端值的机会也变大,①和②的差别也会越来越小。将样本的方差作为总体方差的点估计量,通常用s2表示。
值得一提的是,如果我们有m个样本,在计算这些样本的实际方差时,直接用①;如果是用这些样本估计总体的方差,应该使用②。

估计总体的比例
很多人会在30分钟之内取得报告单,同样也有很多人要等更久。我们可以计算出样本中成功人数(30分钟之内拿到报告的人数)的比例,并用这个比例作为总体概率的点估计量:

到目前为止,点估计仍然很简单,所以经常有人吐槽:概率这么简单的玩意有啥值得研究的?
样本出现的概率
经过多年的统计分析,医院已经明确告知,每个患者都有50%的概率会在30分钟内拿到报告单。我们用p=50%表示总体中所有在30分钟之内拿到报告的人数的占比。如果把一个患者在30分钟之内拿到报告看作成功,用随机变量X表示m个样本中的成功数量,那么X符合参数为m和p的二项分布,X~B(m, p),即成功次数符合试验次数和成功率的二项分布。保持试验次数m不变,二项分布近似于均值为mp、方差为mpq的正态分布(q = 1 - p)。
下面的代码画出了二项分布和其近似的正态分布:
import numpy as np import matplotlib.pyplot as plt from scipy import stats fig = plt.figure(figsize=(10, 6)) plt.subplots_adjust(hspace=0.8, wspace=0.3) # 调整子图之间的边距 p = 0.5 # 每次试验成功的概率 q = 1 - p # 每次试验失败的概率 m_list = [10, 15, 20] # 试验次数 c_list = ['r', 'g', 'b'] # 曲线颜色 m_max = max(m_list) # 二项分布 X~B(m,p) for i, m in enumerate(m_list): ax = fig.add_subplot(3, 2, i * 2 + 1) xs = np.arange(0, m + 1, 1) # 随机变量的取值 ys = stats.binom.pmf(xs, m, p) # 二项分布 X~B(m,p) ax.vlines(xs, 0, ys, colors=c_list[i], label='m={}, p={}'.format(m, p)) ax.set_xticks(list(range(0, m_max + 1, 2))) # 重置x轴坐标 ax.set_xlabel('X') ax.set_ylabel('pmf') ax.set_title('X~B(m, p)') ax.legend(loc='upper right') # 保持二项分布试验的次数m不变,二项分布近似于均值为mp、方差为mp(1-p)的正态分布: for i, m in enumerate(m_list): ax = fig.add_subplot(3, 2, i * 2 + 2) xs = np.arange(0, m + 1, 0.1) # 随机变量的取值 mu, sigma = m * p, (m * p * q) ** 0.5 ys = stats.norm.pdf(xs, mu, sigma) ax.plot(xs, ys, c=c_list[i], label='m={}, p={}'.format(m, p)) ax.set_xticks(list(range(0, m_max + 1, 2))) # 重置x轴坐标 ax.set_xlabel('X') ax.set_ylabel('pdf') ax.set_title('X~N(mp, mpq)') ax.legend(loc='upper right') plt.show()

某天来了20名患者,其中有12人在30分钟之内拿到了报告单(12个成功)。根据二项分布,这种情况出现的概率是:
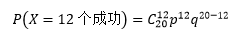
100天过去,每天都有20名患者接受验血,xi人在30分钟内拿到了报告,每天的样本都对应一个概率:
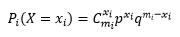
上式中所有mi的数量都是20,之所以用mi表示,是为了强调虽然每天的样本数量一致,但样本本身是不同的。如果将这些概率也看成随机变量,那么这些变量也必然会符合某一个分布,只要弄清这个分布,就能回答产生某个样本的概率。既然可以通过样本知道样本中成功数量的占比,那么这个分布也就等同于“样本中成功数量的占比”的概率。比如第10天的样本中成功数量的占比是p10=45%,我们的目标是了解p10产生的概率有多大,即P(p10)=?换句话说,我们希望知道所有Pi(X=xi)构成的分布。
我们用ps表示某个特定样本中成功数量的占比,借助期望和方差来窥探ps的分布。一个明显的关系是,如果总体中有50%的人可以在30分钟内拿到报告,那么我们也同样期望在样本中看到这个比例,这也是我们能够用样本估计总体的基础。用随机变量X表示样本中成功的数量,ps = X/m:
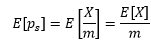
我们已经知道X~B(m, p),这里m是样本数量,p是每个样本成功的概率,是预先给出的。二项分布的期望是E[x] = mp,方差是Var(X)=mpq,q = 1 – p,因此:
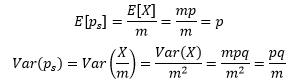
E[ps]告诉我们,样本中成功数量的占比与整体中成功数量的占比一致;Var(ps)告诉我们,m越大,ps的方差越小,样本中成功数量的占比越近总体中成功数量的占比,用ps来估计p越可靠。既然二项分布X~B(m, p)可以由X~N(mp, mpq)来近似,那么ps =X/m也可以由ps~N(p, pq/m)来近似。对于本例来说,p=0.25,pq/m=0.0125:

值得注意的是,比例的分布刻画的是样本成功数占比(即X/m)的变化情况,而二项分布刻画的是特定数量的样本中成功数(即X)的变化情况。比例的取值范围是[0, 1],因此在描述ps的分布时,随机变量的有效取值范围是[0, 1]。当m固定时,每个成功数占比都代表一个特定的样本,我们可以借用ps的分布计算从总体中抽样出某个固定数量样本的概率。
连续性修正
对于二项分布来说,保持试验次数n不变,二项分布近似于均值为np、方差为npq的正态分布。这里特别强调了“近似于”,是因为二项分布的随机变量是离散型的,而正态分布的随机变量是连续型,但是这又有什么关系呢?
这里先要了解一下离散型分布函数和连续型分布函数的特点。对于连续型分布来说,其分布函数是用密度函数的积分表示的:

对于积分来说,a~b的区间与是否包含a点或b点没什么关系,对于连续型随机变量的累积概率来说:
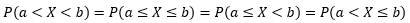
但是上式对于离散型随机变量并不成立。下面是一个离散型分布函数,纵坐标的c.d.f是累积分布函数(cumulative distribution function)的缩写:

上图向我们展示了P(X < 1) = 0,P(X ≤ 1) = 0.5。这意味着对于离散型随机变量来说,经常有P(x ≤ a) ≠ P(x < a)的情况(并不总是不等,这要看a的取值,对于上图来说,P(X < 1.5) = P(X ≤ 1.5)),而连续型随机变量总是有P(x≤a) = P(x<a)。
μ=50,σ2=25的正态分布X~N(μ, σ2)可以用来近似n=100,p=0.5的二项分布X~B(n, p),下图是二者的分布函数(注意这里的曲线是分布函数,而不是密度函数):
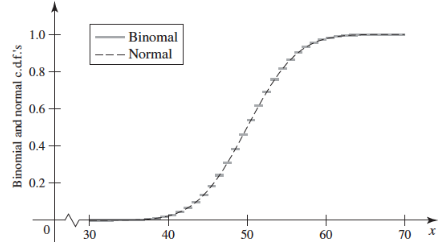
可以看出,由于二项分布的离散型随机变量只能取到整数,因此它的分布函数是阶梯状的,而正态分布的曲线穿过了每个阶梯的中心点,将阶梯分成了两部分,左半部分离散分布大于连续分布,右半部分则相反:

分别用FB(x)=PB(X≤x)和Fn(x)=Pn(X≤x)表示二项分布和正态分布的分布函数,对于整数x来说,在[x, x+0.5)区间内,FB(x) > Fn(x);在(x+0.5, x+1)区间内,FB(x) < Fn(x);只有在中心点,才有FB(x) = Fn(x)。
现在问题来了,用正态分布去做近似的时候,如果直接用FN(x)去近似PB(X<x),那么结果会偏大;如果用FN(x)去近似PB(X≤x),则结果会偏小:
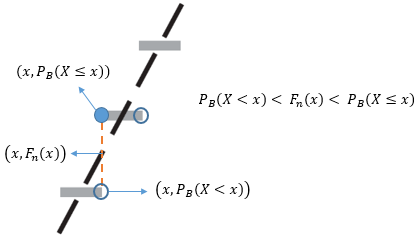
时大时小并不是个好主意,我们想要的是一个一致的近似,要么总是大,要么总是小。一个办法是对于X的正态连续性修正为±0.5,即用FN(x+0.5)去近似PB(X < x)和PB(X ≤ x),得到的结果不会偏小;或用FN(x-0.5)去近似PB(X < x)和PB(X ≤ x),得到的结果不会偏大。这有点类似于用黎曼和计算积分时选用左矩形公式还是右矩形公式:
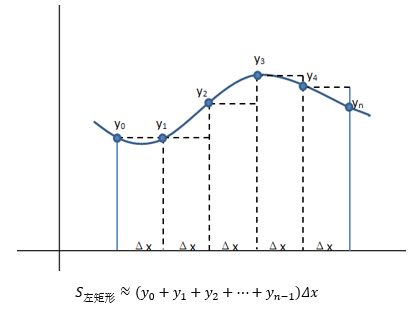
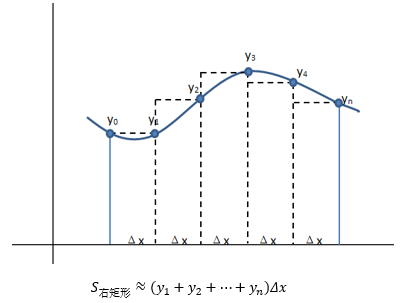
回顾上一节的内容,我们计算出了样本占比ps的正态分布近似,ps的连续性修正为:
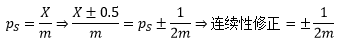
借助连续性修正可以求得:
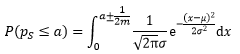
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”



 浙公网安备 33010602011771号
浙公网安备 33010602011771号