概率统计14——几何分布
我家小朋友年方1岁半,家里每天上午都要出去遛小孩。现在小朋友有两项爱好,在家翻垃圾桶,出门捡烟头。
翻垃圾桶可以有效地限制,捡烟头可是防不胜防。
也许烟头能散发出特殊的能量波动,小区的绿化带和草坪上的大部分烟头都能被小朋友准确地发现,如果他在不规则的前进路线中突然停下了,那肯定是看到了新的烟头。

错失奖励概率
在我的严密监视下,小朋友捡烟头的几率已经从原来的“绝不放过”下降到了现在的20%,如果他直到回家还没有烟头,就能得到一个棒棒糖作为奖励。当然,每个烟头对他来说仍然存在着独特的魅力,在最初遇到的3个烟头中没有经受住考验的概率是多少?
设随机变量X是小朋友最终捡起烟头时所发现的烟头个数,那么:

最初遇到的3个烟头中没有抵抗住诱惑的概率可以用P(X ≤ 3)表示:
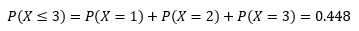
每个烟头都是一次考验,我的关注点是,小朋友在第几次考验时会捡起烟头?
质量函数
小朋友每次遇到烟头的行为都是一个独立的随机试验,试验只有成功和失败两种结果,且对于每个随机试验来说,成功的概率都是相同的。对于小朋友自己来说,捡起烟头是成功,错过才是失败,只要成功一次就没有棒棒糖,试验结束。现在用p表示成功率(捡起烟头的概率),q = 1 – p表示失败率,随机变量X表示第一次成功时所经历的试验次数,那么在进行了r次试验后才遇到第一次成功的概率(或者说在第r次试验取得成功前,需要经历r-1次失败的概率)可以表示为:
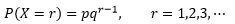
这个分布就是几何分布(Geometric distribution),X服从几何分布,记为X~GE(p)。
下面的python代码展示了r取不同值时的P(X=r)。
1 import numpy as np 2 import matplotlib.pyplot as plt 3 from scipy import stats 4 5 p = 0.2 # 成功率 6 print('X ~ GE({0})'.format(p)) 7 8 rs = np.array(range(1, 11, 1)) # 随机变量的取值 9 # 几何分布 X ~ GE(0.2) 10 ps = stats.geom.pmf(rs, p) # 每个随机变量对应的概率 11 for i, r in enumerate(rs): 12 print('P(X={0})={1}'.format(r, ps[i])) 13 14 plt.bar(left=rs, height=ps, width=0.5) 15 plt.xlabel('r, X=r表示第r次试验才成功') 16 plt.ylabel('P(X=r)') 17 plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 18 plt.show()
X ~ GE(0.2)
P(X=1)=0.2
P(X=2)=0.16000000000000003
P(X=3)=0.12800000000000003
P(X=4)=0.10240000000000003
P(X=5)=0.08192000000000002
P(X=6)=0.06553600000000002
P(X=7)=0.052428800000000025
P(X=8)=0.041943040000000015
P(X=9)=0.033554432000000016
P(X=10)=0.026843545600000015
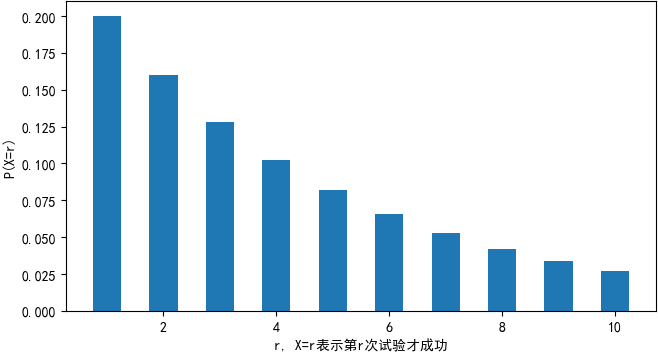
对于几何分布来说,r是大于等于1的自然数,并且只有成功的概率处于(0, 1)之间才有意义,因此当r = 1时,P(X = r)达到最大值,随着r的增大,P(X = r)也越来越小。
几何分布是一个典型的长尾分布,第一次就成功的概率是最高的,这看似有违直觉。这里需要注意的是,“第r次才取得成功”和“在r次之内取得成功”是两回事,后者才是概率越来越大。
实际中有不少随机变量服从几何分布,例如某产品的不合格率为0.05,则首次查到不合格品的检查次数X~GE(0.05)。
分布的形状
现在回到问题的关注点:小朋友在第几次考验时会捡起烟头?这个问题并不能确切地回答,可以回答的是,在r次考验之内捡起烟头的概率。这个概率可以用分布函数表示:
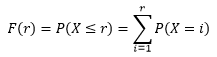
另一种计算方法是:
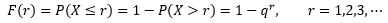
P(X > r)表示在取得第一次成功时,前r次试验都失败的概率。F(r)更为专业的说法是:为得到1次成功而进行r次伯努利试验,r的概率分布。
下面的代码展示了几何分布的形状:
1 fs = stats.geom.cdf(rs, p) # 每个r对应的分布 2 for i, r in enumerate(rs): 3 print('F({0})=P(X<={0})={1}'.format(r, fs[i])) 4 5 plt.bar(left=rs, height=fs, width=0.5) 6 plt.xlabel('r, X<=r表示前r次试验至少有一次成功') 7 plt.ylabel('F(r) = P(X <= r)') 8 plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 9 plt.show()
F(1)=P(X<=1)=0.19999999999999998)
F(2)=P(X<=2)=0.36)
F(3)=P(X<=3)=0.488)
F(4)=P(X<=4)=0.5904)
F(5)=P(X<=5)=0.67232)
F(6)=P(X<=6)=0.7378560000000001)
F(7)=P(X<=7)=0.7902848)
F(8)=P(X<=8)=0.83222784)
F(9)=P(X<=9)=0.865782272)
F(10)=P(X<=10)=0.8926258176)
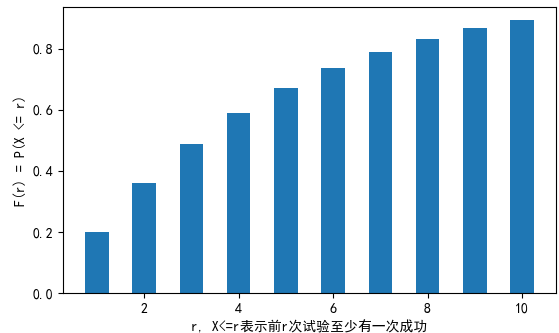
小朋友大约有89%的概率在10次考验内捡起烟头,他也因此很少得到棒棒糖。
期望和方差
X ~ GE(p),q=1-p,P(X = r) = pqr-1,当r→∞时:
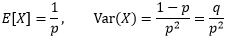
来看看是怎么得出的。
期望

可以根据几何级数的公式继续计算:
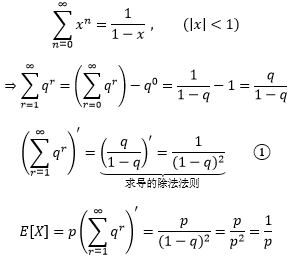
对于几何分布来说,p=0.2表示单次试验成功的概率是0.2,E[X]=1/p=5是在告诉我们,期望在第5次试验时获得成功,或者说5次试验中就有一次趋向成功。
方差
根据Var(X) = E[X2] – E[X]2来计算几何分布的方差:

将①代入:
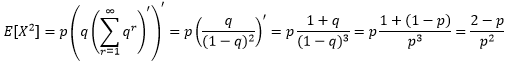
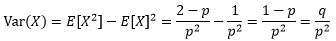
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”



 浙公网安备 33010602011771号
浙公网安备 33010602011771号