概率笔记10——矩估计和最大似然
估计
生活中我们经常估计一些数值，比如从家到学校要走多久？一颗大白菜大概多少斤？凭什么估计出具体数值呢？“估计”不是瞎猜，是根据已有数据计算的。从家到学校往返过多次，手上也拿过无数颗白菜，此时我们会凭借心中的尺度计算出一个大约的数值。
矩估计
矩估计，即矩估计法，也称“矩法估计”，是利用已有样本估计期望值的一种方法。
某个问题的数学期望客观存在的数学特征，是一个具体的数值，只是这个数值计算起来需要知道一些“已知条件”，而这些已知条件在现实世界中并不可知。幸运的是，我们可以随时得到一些随机样本，利用这些样本估计一个数值：
戴帽子的等号表示估计。每个xi都是一个简单随机样本，并且我们认为每个样本都是等可能的，这实际上是真实世界中一种不得已而为之的办法。在大数定律下的作用下，这个估计将会逐渐稳定，逼近真实值。
现在有甲、乙两个射击运动员站在我们面前，他们的平均成绩并没有贴在身上，如何判断他们的成绩呢？
一个符合经验的做法是让他们各打10枪，然后计算均值。比如xi是甲第i枪的成绩，那么我们对甲的估计是(x1+x2+…+x10)/10。这里使用的是简单的均值，并没有任何概率参与，原因是我们并不知道甲打出每一环的概率，只好认为是等权平均。数学期望是运动员的真实成绩，我们在计算数学期望时需要已知运动员打出每一环的概率，然而“已知”在并不总是存在于现实世界，因此才退而求其次，使用“估计”。
独立同分布
独立同分布是概率论中的一个概念，即一组数据彼此间互不干扰，在现实环境里随机出现。
独立已经介绍过多次，射击比赛中的每一次射击都是独立的，不会因为本次的结果影响下一枪（抛开运动员心理状态的变化）。如果是从一堆白球中取一个黑球，随着白球的减少，下次取出黑球的概率会不断变大，则不能称每次的取球行为相互独立。
“同分布”的意思是每次都从特定的集合中取结果，比如掷骰子，每次都从1~6中取结果，则称样本是同分布。如果夹杂着几个12面的骰子，则样本不是同分布的。
未知的密度函数
在连续型变量中，只要我们知道变量的概密度f(x)，就可以知道它的期望：
问题是f(x)通常是未知的，只知道它的模型，但不确定具体的模型参数。我们设这个未知的参数是θ，概率密度是f(x;θ)，表示f受到θ的影响，数学期望公式：
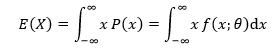
实际上θ是一个向量，例如：
示例 设连续型随机变量的概率密度是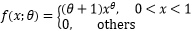 
，求θ的矩估计量。
可以先计算出X的矩估计：
只有0<x<1的时候才能计算θ：
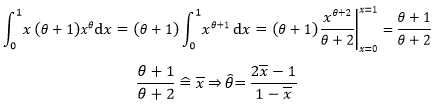
最大似然
最大似然估计方法（Maximum Likelihood Estimate，MLE）也称为最大概似估计或极大似然估计，是建立在最大似然原理的基础上的一种统计方法。
最大似然的含义
“似然”就是“可能性”的意思。我们经常听到“最大似然”，这个词来源于实际，下图解释了它的含义。
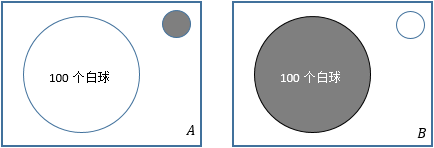
A、B是两个一模一样的箱子，A中有100个白球和1个黑球，B中有100个黑球和1个白球。现在从两个箱子中随意取出一个小球，结果是黑球，这个黑球是从哪个箱子中取出的？第一反应是“最有可能从B中取出的”，这符合通常的经验。这里的“最有可能”就是“最大似然”的意思。
似然和似然函数
假设有一个独立同分布的数据集X，它的参数是θ。现在从X中取出一些样本x={ x1, x2, …, xn}，P(x;θ)表示给定参数θ时，从X中取得这些样本x的可能性：
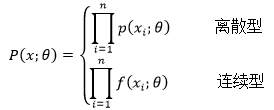
其中P(x;θ)类似于条件概率，但不等于条件概率，因为θ只是一个密度函数中的参数，并不是一个事件。
假设现在θ有两个取值θ1和θ2，对于X中的一些样本x={ x1, x2, …, xn}，如果P(x, θ1 )> P(x, θ2 )，就认为θ1对产生x的可能性（似然性）要大于θ2，P(x, θ1 )和P(x, θ2)就是似然，是对参数θ产生样本x的可能性的度量。
还是以射击为例，假设按运动员的成绩由高到低分为一级、二级、三级，甲打出了10枪x={9,9,10,10,8,9,9.5,9.5,9.5,9}。运动员的级别相当于影响成绩的参数θ，当θ等于一级时，甲打出这个成绩的可能性较高。
现在需要根据给定样本x来求P(x; θ)，由于样本是已知的，将所有x的值代入上面的公式，将得到一个只有θ的式子，这个式子称为θ的似然函数，记为L(x;θ)或L(θ)：
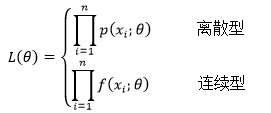
最大似然估计
知道了似然函数，最大似然估计就很容易理解了：对于一个给定的样本集，挑选使得P(x;θ)能够达到最大时的参数 作为θ的估计值，使得：
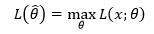
最终将求得θ的一个估值 ，在 时，似然函数的值最大。
极值点通常是在导数等于0的点取得，因此可以通过下式求得θ：
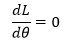
如果θ是n维向量，则：
对于一些特殊的密度函数（比如指数密度函数）来说，直接求dL/dθ太过繁琐，由于L与lnL在同一θ处取到极值，所以也经常使用：
示例
示例1
设样本的总体分布率为：P{X=x}=px(1-p)1-x，求p在观察样本{ x1, x2, …, xn }下的最大似然估计量。
这里只不过是把θ用p表示，现在我们做一下替换，变成熟悉的形式：
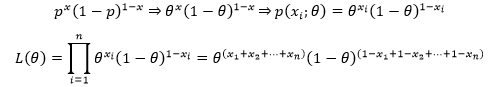
L(θ)是θ的指数形式，换成对数更为简单：
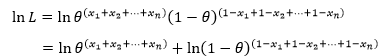
根据对数的基本公式继续计算：
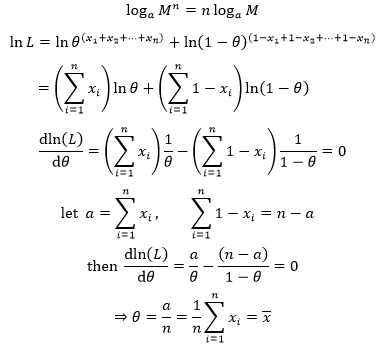
示例2
总体样本服从参数为λ的指数分布，{x1, x2, …, xn}是观察样本，求λ的最大似然估计值。
总体样本的概率密度是：
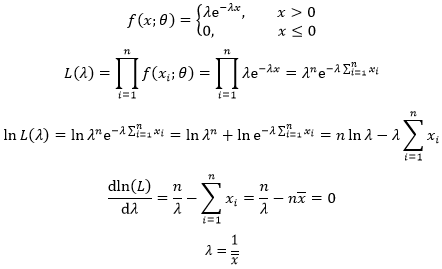
作者：我是8位的
出处：http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注公作者众号“我是8位的”
