异常检测(1)——局部异常因子算法
局部异常因子算法(Local Outlier Factor)通过计算“局部可达密度”来反映一个样本的异常程度,一个样本点的局部可达密度越大,这个点就越有可能是异常点。
k距离和k距离邻域
某一点P的k距离(k-distance)很容易解释,就是点P和距离点P第k近的点之间距离,但不包括P。假设P是学校,葛小伦、刘闯、赵信、蔷薇、琪琳、炙心6个同学都住在学校附近:
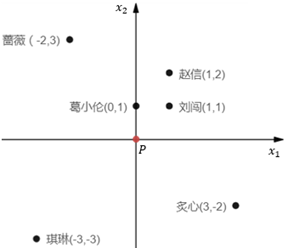
图1
为了简单前起见,将P放置在原点。用欧几里得距离表示每个同学的家到学校的距离,由近及远分别是葛小伦<刘闯<赵信<蔷薇=炙心<琪琳,距P最近的是葛小伦,第2近的是刘闯,第3近的是赵信,第4近的是蔷薇和炙心,第5近的是琪琳。
当k=t时,在数据集中用下式表示x(i)的k距离,其中x(k=t)表示距x(i)第k远的数据样本:

所谓P的k距离邻域(k-distance neighborhood of p),就是到P的直线距离小于P的k距离的所有数据样本构成的集合。在图9.1中,当k=3时,P的k距离邻域是{葛小伦、刘闯、赵信};当k=4时,P的k距离邻域是{葛小伦、刘闯、蔷薇、炙心}。
可以把P看作圆心,把P的k距离看作半径做一个圆,圆中的样本点就是P的k距离邻域:
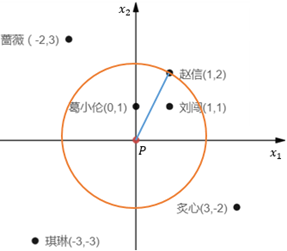
图2
可达距离
x(i)到x(j)的可达距离(Rechabiliby Distance)可以表示为:
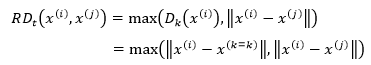
它的含义是,当x(i)距x(j)的距离比x(i)距x(k=t)更近时,直接用数值较大的|| x(i)- x(k=k)||表示x(i)到x(j)的可达距离,否则用|| x(i)- x(j)||表示。
以图1为例,当k=3时,距P第3近的同学是赵信,P的k距离邻域是{葛小伦、刘闯、赵信},则P到他们的可达距离都等于学校到赵信家的距离;P到蔷薇、炙心、琪琳的可达距离与学校到她们的实际距离相等:
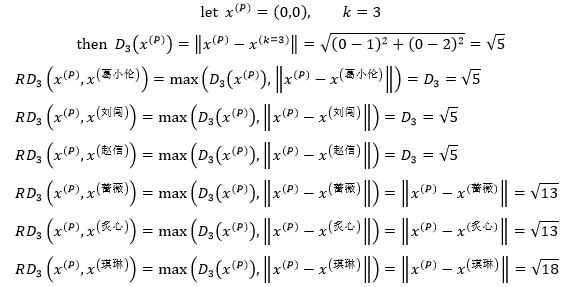
由于以x(i)的k近距离和x(j)的k距离并不相等,所以x(i)到x(j)的可达距离和x(j)到x(i)的可达距离并不相等:
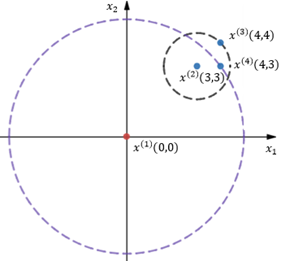
图3
在图3中,当k=2时,先计算x(1)到x(2)的可达距离,此时距x(1)第2近的点是x(4):
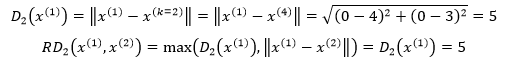
再来看看x(2)到x(1)的可达距离,距x(2)第2近的点是x(3):
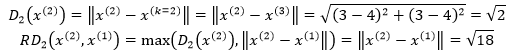
由此可见:
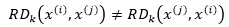
局部可达密度
点与点之间的密度很容易理解,点之间距离越远,密度越低,距离越近,密度越高。局部可达密度与总体密度类似,只不过是用k距离邻域计算的,所以称为“局部”。
假设x(i)的k距离邻域中有N个样本点,用xN表示,xN(t)表示xN中的第t个样本点,那么x(i)的局部可达密度(local reachability density)可以写成:
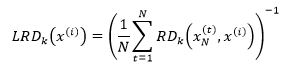
上式中x(i)的局部可达密度是x(i)的k距离邻域中所有样本点到x(i)的可达距离的平均值的倒数。 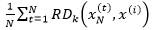 代表xN中样本点的密集程度,密集程度越高,该值越小,它的倒数(x(i)的局部可达密度)的值越大,x(i)和xN越可能是同一簇;反之,如果x(i)是异常数据,那么xN中的样本点到x(i)的可达距离将会取这些样本点到x(i)的直线距离,这个距离将远大于xN中样本点的k距离,最终导致
代表xN中样本点的密集程度,密集程度越高,该值越小,它的倒数(x(i)的局部可达密度)的值越大,x(i)和xN越可能是同一簇;反之,如果x(i)是异常数据,那么xN中的样本点到x(i)的可达距离将会取这些样本点到x(i)的直线距离,这个距离将远大于xN中样本点的k距离,最终导致 较大,它的倒数(x(i)的局部可达密度)的值较小。简单而言,x(i)的局部可达密度越大,x(i)越靠近它邻域中的点;x(i)的局部可达密度越小,x(i)越远离它邻域中的点。
较大,它的倒数(x(i)的局部可达密度)的值较小。简单而言,x(i)的局部可达密度越大,x(i)越靠近它邻域中的点;x(i)的局部可达密度越小,x(i)越远离它邻域中的点。
局部异常因子
有了局部可达密度,就可以进一步定义局部异常因子(local outlier factor):
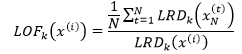
上式的分子表示x(i)的k距离邻域中的所有样本点的局部可达密度的均值,分母是x(i)的局部可达密度。它实际上是通过比较x(i)的密度和其邻域的密度来判断x(i)是否是异常点,x(i)的密度越低,LRDk(x(i))越小,LOFk(x(i))的值越大,x(i)越可能是异常点;x(i)的密度越高,LRDk(x(i))越大,LOFk(x(i))的值越接近1或小于1,x(i)越可能是正常的样本点。
算法实现
我们已经介绍了局部异常因子算法,来看看它是如何工作的。先来创建一些测试数据:
1 import numpy as np 2 import matplotlib.pyplot as plt 3 4 def create_train(): 5 np.random.seed(42) # 设置seed使每次生成的随机数都相等 6 # 生成100个2维数据,它们是以0为均值、以1为标准差的正态分布 7 X_inliers = 0.3 * np.random.randn(100, 2) 8 # 构造两组间隔一定距离的样本点作为训练数据 9 X_inliers = np.r_[X_inliers + 2, X_inliers - 2] 10 # 构造20个可能的异常数据,从一个均匀分布[low,high)中随机采样 11 X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2)) 12 # 将X_inliers和X_outliers连接起来作为训练集 13 return np.r_[X_inliers, X_outliers] 14 15 def display(X): 16 plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 17 plt.rcParams['axes.unicode_minus'] = False # 解决中文下的坐标轴负号显示问题 18 plt.title("局部异常因子(LOF)") 19 plt.scatter(X[:, 0], X[:, 1], color='k', s=3., label='样本点') 20 21 plt.axis('tight') # 让坐标轴的比例尺适应数据量 22 plt.xlim((-5, 5)) # x坐标轴的刻度范围 23 plt.ylim((-5, 5)) # y坐标轴的刻度范围 24 # plt.xlabel("预测误差数: %d" % (n_errors)) 25 legend = plt.legend(loc='upper left') 26 legend.legendHandles[0]._sizes = [10] 27 plt.show()
create_train()创建了一个数据集,这个数据集中包含了两簇正常的样本和20个可能的异常样本,之所以是“可能的异常样本”,是由于X_outliers中的数据是随机采样的,可能靠近正常的样本簇:
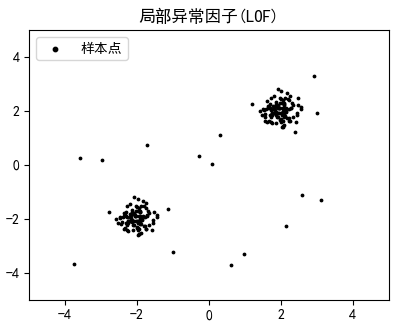
接下来按照前面的介绍依次实现数据集中每一个样本的k距离、k距离邻域、可达距离、局部可达密度和局部异常因子,并修改display(),将每个样本点的异常因子标记在图像上。完整代码:
1 import numpy as np 2 import matplotlib.pyplot as plt 3 4 def create_train(): 5 np.random.seed(42) # 设置seed使每次生成的随机数都相等 6 # 生成100个2维数据,它们是以0为均值、以1为标准差的正态分布 7 X_inliers = 0.3 * np.random.randn(100, 2) 8 # 构造两组间隔一定距离的样本点作为训练数据 9 X_inliers = np.r_[X_inliers + 2, X_inliers - 2] 10 # 构造20个可能的异常数据,从一个均匀分布[low,high)中随机采样 11 X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2)) 12 # 将X_inliers和X_outliers连接起来作为训练集 13 return np.r_[X_inliers, X_outliers] 14 15 def display(X): 16 plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 17 plt.rcParams['axes.unicode_minus'] = False # 解决中文下的坐标轴负号显示问题 18 plt.title("局部异常因子(LOF)") 19 plt.scatter(X[:, 0], X[:, 1], color='k', s=3., label='样本点') 20 21 max_lof, min_lof = max(LOF), min(LOF) 22 # 每个样本点的半径,样本点越异常,半径越大(归一化处理) 23 radius = [1000 * ((x - min_lof) / (max_lof - min_lof)) for x in LOF] 24 plt.scatter(X[:, 0], X[:, 1], s=radius, edgecolors='r', facecolors='none', label='异常度') 25 26 plt.axis('tight') # 让坐标轴的比例尺适应数据量 27 plt.xlim((-5, 5)) # x坐标轴的刻度范围 28 plt.ylim((-5, 5)) # y坐标轴的刻度范围 29 # plt.xlabel("预测误差数: %d" % (n_errors)) 30 legend = plt.legend(loc='upper left') 31 legend.legendHandles[0]._sizes = [10] 32 legend.legendHandles[1]._sizes = [20] 33 plt.show() 34 35 D_K = [] # X中每个样本点的k距离 36 NEIGHBORS = [] # X中每个样本点的k距离邻域 37 LRD = [] # X中每个样本点的局部可达密度 38 39 def euclid(x_i, x_j): 40 # 两点间的欧几里得距离 41 return np.linalg.norm(x_i - x_j) 42 43 def all_D_k(X, k): 44 for x_i in X: 45 # x_i距所有样本点的欧几里得距离 46 x_and_d = [(x_j, euclid(x_i, x_j)) for x_j in X if (x_i != x_j).any()] 47 x_and_d = sorted(x_and_d, key=lambda x: x[1]) # 按照距离排序 48 D_K.append(x_and_d[k - 1][1]) # x_i的k距离,此处假设x_and_d中没有重复的距离 49 NEIGHBORS.append([x for x, d in x_and_d[:k]]) # x_i的k距离邻域 50 for x_i in X: # 计算每个样本点的局部可达密度 51 neighbors = neighbors_k(x_i, X, k) # x_i的k邻域 52 LRD.append(1 / (sum([rd(x_t, x_i, X, k) for x_t in neighbors]) / len(neighbors))) 53 54 def d_k(x, X, k): 55 # x的k距离 56 i = np.argwhere(X == x)[0, 0] # x在训练样本中的索引 57 return D_K[i] 58 59 def neighbors_k(x, X, k): 60 # x的k距离邻域 61 i = np.argwhere(X == x)[0,0] # x在训练样本中的索引 62 return NEIGHBORS[i] 63 64 def rd(x_i, x_j, X, k): 65 # x_i到x_j的可达距离 66 return max(d_k(x_i, X, k), euclid(x_i, x_j)) 67 68 def lrd(x, X, k): 69 # x的局部可达密度 70 i = np.argwhere(X == x)[0, 0] # x在训练样本中的索引 71 return LRD[i] 72 73 def lof(X, k): 74 # 数据集中每个数据样本的局部异常因子 75 LOF = [] 76 for i, x_i in enumerate(X): 77 neighbors = neighbors_k(x_i, X, k) # x_i的k邻域 78 LOF.append(sum([lrd(x_t, X, k) for x_t in neighbors]) / len(neighbors) / lrd(x_i, X, k)) 79 return LOF 80 81 if __name__ == '__main__': 82 X = create_train() 83 k = 20 84 all_D_k(X, k) # 计算X中每个样本点的第k近的距离 85 LOF = lof(X,k) 86 display(X) 87 88 for i, lof in enumerate(LOF): 89 print(lof, '\t', end='') 90 if (i + 1) % 7 == 0: 91 print()
all_D_k将每个样本点的k距离、k距离邻域、局部可达密度缓存起来,以便后续计算局部异常因子时避免大量重复运算。
每个样本的圆代表了该点的局部异常因子,圆的半径越大,该点越倾向于异常点:
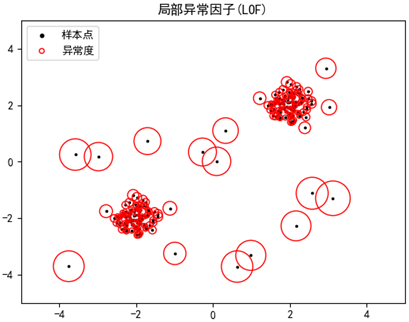
程序最后还显示了每个样本点的异常因子,最后20个样本的局部异常因子比其它值更大于1:
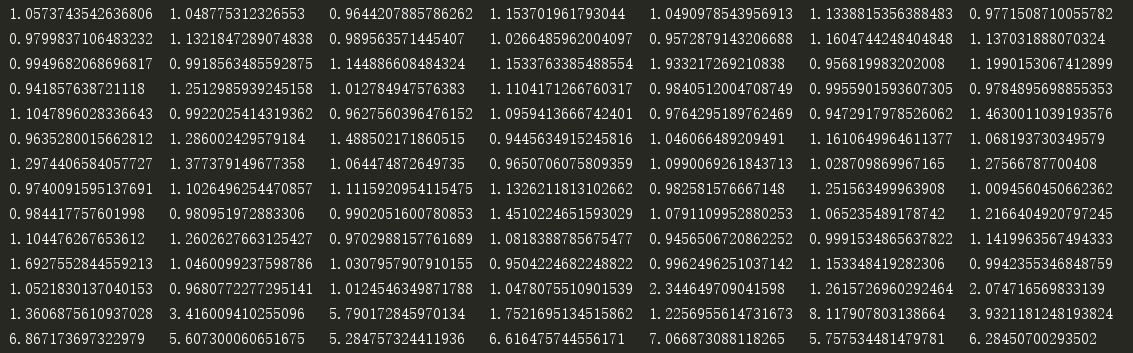
在实际应用中,可以让所有异常因子和一个自定义的阈值比较,如果LOF(x(i))大于该阈值,则认为x(i)是异常数据。
sk-lean中有关于局部异常因子的模块,可参考官方的示例:
https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.LocalOutlierFactor.html
作者:我是8位的



 浙公网安备 33010602011771号
浙公网安备 33010602011771号