递归的逻辑(4)——递归与分形
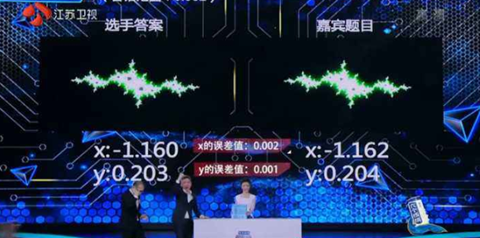
《最强大脑》第四季的一期节目中,挑战者余彬晶挑战的项目是“分形之美”。这是一个数学推理项目,章子怡女神和不懂球的胖子都一脸迷茫。
分形的概念
分形(Fractal)一词,是曼德布罗特创造出来的,其原意具有不规则、支离破碎等意义,分形几何学是一门以非规则几何形态为研究对象的几何学。由于不规则现象在自然界是普遍存在的,因此分形几何又称为描述大自然的几何学。
分形通常被定义为“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状,即具有自相似的性质。”
分形图无处不在,绵延的海岸线,从远距离观察,其形状是极不规则的,但是从近距离观察,其局部形状又和整体形态相似;一颗参天大树,它的每一片叶子和枝干,都和主枝显现出了高度的相似性;一片雪花的每片花瓣都在放大后都显出了原图案惊人的相似性。

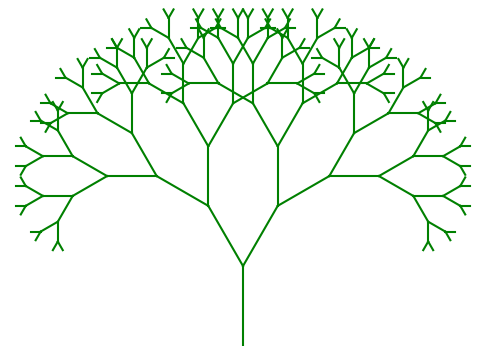
既然分形图的每一部分都是整体的缩小,那么很自然地会联想到自身调用自身的程序。我们尝试用递归去绘制一颗分形树,下图是绘制的目标:
极坐标系下的向量旋转
虽然绘制的目标是二维图形,但是比起刻度尺来,树的坐标关系要复杂的多,继续在直角坐标系下处理就显得有点笨拙了,此时不妨试试极坐标。
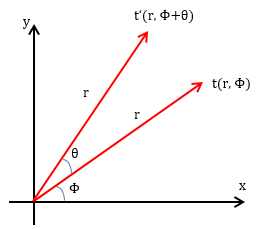
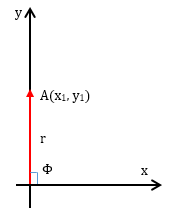
极坐标用向量的长度和角度来表示坐标中的点,一个典型的极坐标如下:

r是向量的长度,φ是向量与x轴逆时针方向的夹角,点t可以用(r,φ)来表示。可以看出,极坐标系仍未脱离原来的直角坐标系,仅仅是将直角坐标系上的点换了一种表示法,如果将点t 转换成直角坐标系的表示法,那么:

这也是极坐标到直角坐标的转换公式。
接下来将向量逆时针旋转θ,得到新的t’点:
t’点的坐标:
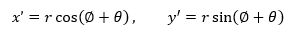
树的主干垂直于x轴,简单起见,可以让它附着在y轴上,这相当于φ等于90°:
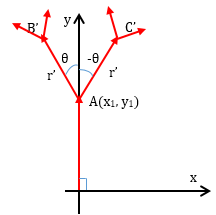
接下来,把一个稍短的向量r’向左旋转θ角得到点B,向右旋转-θ角得到点C:

如此一来可以得到B和C的坐标:
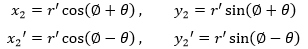
作为树的枝干,还需要将两个新向量上移,让它们以A为起点:
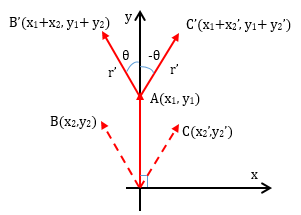
现在得到了树的两个枝干以及枝干端点的坐标:
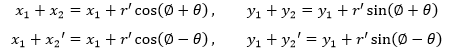
继续按照上述方法进行下去将会得到更多的枝干:
编写代码
知道原理后就可以编写相关代码:
1 class Fractal: 2 def __init__(self, fai, theta, depth): 3 ''' 4 分形图的基础形状 5 Attributes: 6 fai: 向量的初始角度 7 theta: 向量每次逆时针旋转的角 8 depth: 树的深度, 当depth == 0时停止分形 9 ''' 10 self.fai = fai 11 self.theta = theta 12 self.depth = depth 13 14 def draw(self, ax): 15 def draw_line(x1, y1, fai, depth, ax): 16 if depth == 0: 17 return 18 # 由于np.cos和np.sin使用的参数是弧度,所以需要先把角度转换成弧度 19 radian = np.radians(fai) 20 # 旋转后的坐标 21 x2 = x1 + np.cos(radian) * depth 22 y2 = y1 + np.sin(radian) * depth 23 ax.plot([x1, x2], [y1, y2], color='g') 24 draw_line(x2, y2, fai + self.theta, depth - 1, ax) 25 draw_line(x2, y2, fai - self.theta, depth - 1, ax) 26 draw_line(0, 0, self.fai, self.depth, ax) 27 28 if __name__ == '__main__': 29 fig, ax = plt.subplots() 30 plt.axis('off') 31 plt.axis('equal') 32 fractal = Fractal(90, 30, 8) 33 fractal.draw(ax) 34 plt.show()
我们用数的深度表示向量的长度,每一层枝干的长度都比上一层少1,直到深度是0为止。每一层枝干都是由上一层枝干的终点坐标、偏斜角和枝干长度决定的。fai的初始值是90°,用draw_line(0, 0, 90, depth)来画树的主干,这样才能保证主干是附着在y轴上,主干的终点坐标:
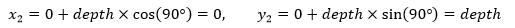
弧度和角度的转换公式是1rad=180°/π,π是无限不循环小散,因此python中这个转换是不精确的。如果直接运行np.cos(np.radians(90)),不会得到0,而是得到6.123233995736766e-17,这是一个相当小的数,可以当作0处理。
运行结果如下:
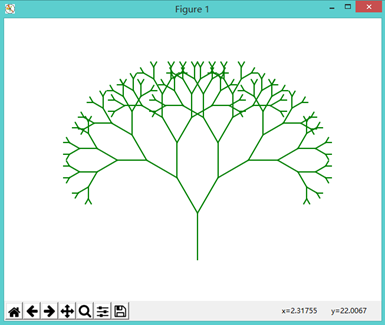
可以通过改变初始深度来观察树的分型过程:
if __name__ == '__main__': # 观察分形过程 fig = plt.figure() for i in range(1, 9): ax = fig.add_subplot(3, 3, i) fractal = Fractal(90, 30, i) plt.axis('off') plt.axis('equal') plt.title('depth=' + str(i)) fractal.draw(ax) plt.show()
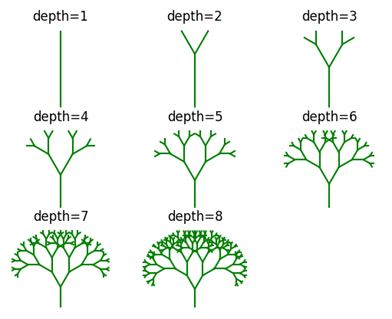
在绘制depth =1的分形树时,代码中plt.axis('equal')这句话是必须的,它将使x轴和y轴的定标系数相同,即单位长度相同。如果将其注释掉,由于角度和弧度间的不精确转换,将得到一条斜线:
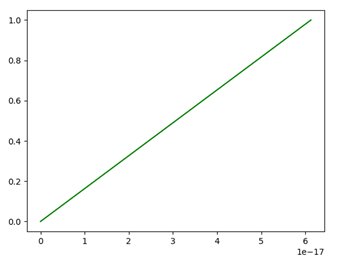
斜线是根据(0,0)和(6e-17, 1)绘制的。在添上plt.axis('equal')后,这个微小的斜率就可以忽略不计了:

通过改变旋转角,可以得到一些有趣的分形:
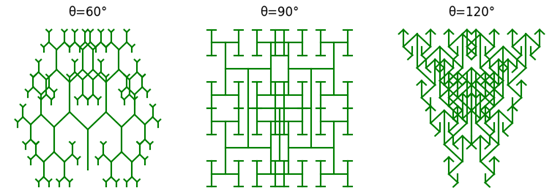
作者:我是8位的



 浙公网安备 33010602011771号
浙公网安备 33010602011771号