递归的逻辑(2)——特征方程和递归算法

递归关系的基本解法

　　无论是fabo_2还是fabo_3，在计算时都需要遵守递归表达式，即求f(n)的值时必须先求得n之前的所有序列数。这就让我们有了一个设想，能否将斐波那契数列的递归表达转换成普通的函数映射？这样就可以在常数时间内求得f(n)。

特征方程和特征根

　　首先要明确的是，没有一个通用的方法能够解所有的递归关系，但是一些解法对于某些规则的递归相当有效，其中的特征方程法就可以用来求得斐波那契数列的显示表达。

　　当一个递归关系满足：

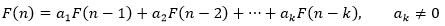
　　则称递归关系为k阶的线性（所有F的次数都是1）常系数（a₁,a₂,...,a_k都是常数）齐次（每一项F次数都相等，没有常数项）递归关系。

　　我们的目标是寻找递归关系的显示表达，这就相当于寻找一个能够表达F(n)函数，令这个函数是：

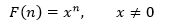
　　根据递归表达式：

　　这就使问题变成了解方程问题，这个方程称为递归关系的特征方程。方程会产生k个跟x₁,x_2,…,x_k，这些跟称为特征根或特征解，当特征解互不相同时，则递归关系的通解是：

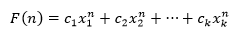
　　其中c₁,c₂,…,c_k是常数，只要求得这些常系数就得到了通解的固定形态。

　　注：这种方法仅适用于没有重跟的常系数线性齐次递归关系。

斐波那契的显示表达式

　　斐波那契数列正好是常系数线性齐次递归关系，因此可以转换为下面的特征方程：

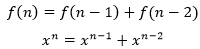
　　接下来是求解特征根：

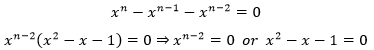
　　由于已经知道在斐波那契数列中x > 0，所以x^n-2≠0，结果只能是x²-x-1=0，这就可以计算出两个特征根：

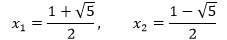
　　两个特征根互不相同，f(n)的通解满足：

　　由于已知f(0)=f(1)=1，因此可以将通解转换为方程组：

　　终于可以求得斐波那契数列的显示表达了：

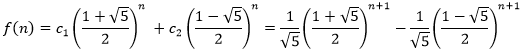
　　这是个很神奇的表达，用无理数表示了有理数。这样斐波那契数列的代码就更直接了：

import math

# 直接利用显示公式计算斐波那契数列
def fabo_2(n):
    f = (((math.sqrt(5) + 1) / 2) ** (n + 1) - ((math.sqrt(5) - 1) / 2) ** (n + 1)) / math.sqrt(5)
    f = round(f, 1)
    if f > int(f):
        return int(f) + 1
    else:
        return int(f)

if __name__ == '__main__':
    for i in range(0, 14):
        print('f({0}) = {1}'.format(i, fabo_2(i)))

　　Python直接使用显示公式将会得到一个浮点数，因此必须额外加上5~9行的处理。

黄金分割

　　现在对斐波那契数列的f(n)求极限：

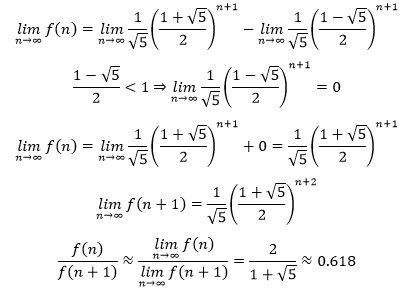
　　这就是著名的黄金分割，一个兔子繁殖的故事最终居然和黄金分割点联系到一起，是不是有些不可思议？

递归算法

　　我们已经见识过不少递归程序，它提供了一种解决复杂问题的直观途径，这一节我们将看到更多关于递归的算法。

可疑的递归

　　在程序设计中递归的简单定义是一个能调用自身的程序，然而程序不能总是调用自身，否则就没有办法停止，所以递归还必须有一个明确的终止条件；另一个指导原则是——每次递归调用的参数值必须更小。

　　看看下面的程序是否是合理的递归？

# 可疑的递归
def suspicious(n, k):
    print('\t' * k, 'suspicious({0})'.format(n))
    if n == 1:
        return 1
    elif n & 1 == 1:
        return suspicious(n * 3 + 1, k + 1)
    else:
        return suspicious(n // 2, k + 1)

if __name__ == '__main__':
    suspicious(3, 0)

　　如果参数n是奇数，suspicious使用3n+1来调用自身；如果n是偶数，使用n/2来调用自身。显然并不是每次都使用更小的参数调用自身，这不符合递归的原则，我们也没法使用归纳法来证明整个程序是否会终止。

　　代码的运行结果：

　　虽然对于suspicious(3)来说，它最后终止了，但我们无法证明它是否会对某个参数有任意深度的嵌套。为了避免不必要的麻烦，还是让递归程序更明确一点——每次递归调用的参数值都更小。

动态编程

　　斐波那契的递归代码很优美，它能够让人以顺序的方式思考，然而这段代码只能作为递归程序的演示样品，并不能应用于实践。在运行时便会发现，当输入大于30时速度会明显变慢，普通家用机甚至无法计算出f(50)。可以通过运行下面的代码清晰的看到变慢的原因：

def fabo_test(n):
    if n < 2:
        return 1
    else:
        print('\t' * (6 - n), 'f({0})'.format(n))
        return fabo_test(n - 1) + fabo_test(n - 2)
if __name__ == '__main__':
    fabo_test(6)

　　第二次递归会忽略上一次所做的所有计算，所以很不给面子的出现了大量重复，这将导致相当大的开销。这段代码说明的问题是，写一个简单而低效的递归方法是相当容易的，我们需要小心这种陷阱。

　　知道问题的所在就可以对症下药，只要把计算过的数据存储起来就好了，这种方法称为动态编程，它消除了重复计算，适用于任何递归计算，能够把算法的运行时间从指数级改进到线性级，其代价是我们可以负担得起缓存造成的空间开销，是典型的空间换时间。

# 存储所有计算过的斐波那契数
fabo_list = [1, 1]
# 用递归计算斐波那契序列
def fabo_4(n):
    if n < len(fabo_list):
        return fabo_list[n]
    else:
        fabo_n = fabo_4(n - 1) + fabo_4(n - 2)
        fabo_list.append(fabo_n)

        return fabo_n

if __name__ == '__main__':
    for i in range(40, 51):
        print('f({0}) = {1}'.format(i, fabo_4(i)))

　　运行结果：

小偷的背包

　　一个小偷撬开了一个保险箱，发现里面有N个大小和价值不同的东西，但自己只有一个容量是M的背包，小偷怎样选择才能使偷走的物品总价值最大？

　　假设有5个物品A,B,C,D,E，它们的体积分别是3,4,7,8,9，价值分别是4,5,10,11,13，可以用矩形表示体积，将矩形旋转90°后表示价值：

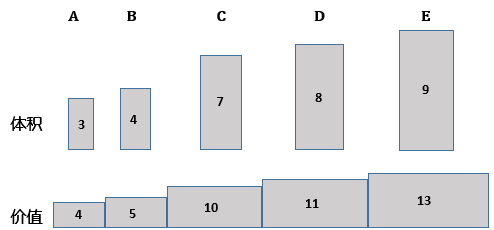
　　下图展示一个容量为17的背包的4中填充方式，其中有两种方式的总价都是24：

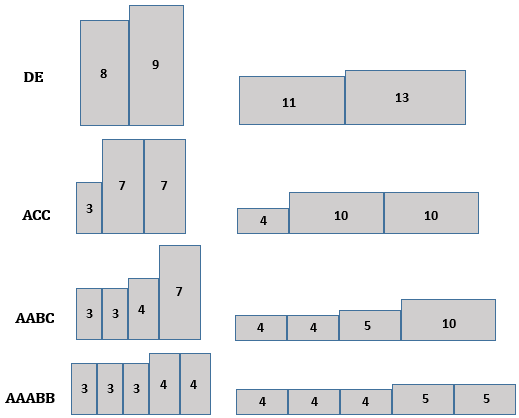
　　背包问题有很多重要的实应用，比如长途运输时，需要知道卡车装载物品的最好方式。我们基于这样的思路去解决背包问题：在取完一个物品后，找到填充背包剩余部分的最佳方法。对于一个容量为M的背包，需要对每一种类型的物品都推测一下，如果把它装入背包的话总价值是多少，依次递归下去就能找到最佳方案。这个方案的原理是，一旦做出了最佳选择就无需更改，也就是说一旦知道了如何填充较小容量的背包，则无论下一个物品是什么，都无需再次检验已经放入背包中的物品（已经放入背包中的物品一定是最佳方案）。

　　可以根据这种方案编写代码：

class Goods:
    ''' 物品的数据结构  '''
    def __init__(self, size, value):
        '''
        :param size: 物品的体积
        :param value: 物品的价值
        '''
        self.size = size
        self.value = value

def fill_into_bag(M, goods_list):
    '''
    填充一个容量是 M 的背包
    :param M: 背包的容量
    :param goods_list: 物品清单，包括每种物品的体积和价值，物品互不相同
    :return: (最大价值，最佳填充方案)
    '''
    space = 0       # 背包的剩余容量
    max = 0         # 背包中物品的最大价值
    plan = []       # 最佳填充方案

    for goods in goods_list:
        space = M - goods.size
        if space >= 0:
            # 在取完一个物品（goods）后，填充背包剩余部分的最佳方法
            space_plan = fill_into_bag(space, goods_list)
            if space_plan[0] + goods.value > max:
                max = space_plan[0] + goods.value
                plan = [goods] + space_plan[1]

    return max, plan

def paint(plan):
    print('最大价值：' + str(plan[0]))
    print('最佳方案：')
    for goods in plan[1]:
        print('\t大小：{0}\t价值：{1}'.format(goods.size, goods.value))

if __name__ == '__main__':
    goods_list = [Goods(3, 4), Goods(4, 5), Goods(7, 10), Goods(8, 11), Goods(9, 13)]
    plan = fill_into_bag(17, goods_list)
    paint(plan)

　　运行结果：

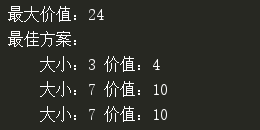
　　遗憾的是，fill_into_bag方法同样只能作为一个简单的试验样品，它犯了和fabo_test同样的错误，第二次递归会忽略上一次所做的所有计算，要花指数级的时间才能计算出结果！为了把时间降为线性，需要使用动态编程技术对其进行改进，把计算过的值都缓存起来，由此得到了背包问题的2.0版，当然，我们并不想把这个算法告诉小偷：

# 字典缓存，space:(max,plan)
sd = {}
def fill_into_bag_2(M, goods_list):
    '''
    填充一个容量是 M 的背包
    :param M: 背包的容量
    :param goods_list: 物品清单，包括每种物品的体积和价值，物品互不相同
    :return: (最大价值，最佳填充方案)
    '''
    space = 0       # 背包的剩余容量
    max = 0         # 背包中物品的最大价值
    plan = []       # 最佳填充方案

    if M in sd:
        return sd[M]

    for goods in goods_list:
        space = M - goods.size
        if space >= 0:
            # 在取完一个物品（goods）后，填充背包剩余部分的最佳方法
            print(goods.size, space)
            space_plan = fill_into_bag_2(space, goods_list)
            if space_plan[0] + goods.value > max:
                max = space_plan[0] + goods.value
                plan = [goods] + space_plan[1]
    # 设置缓存，M空间的最佳方案
    sd[M] = max, plan

    return max, plan

　　

---

　　 作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”