最长公共子序列 LCS

今天退役了，根据惯例要写一篇小作文，如果你能能读完这篇小作文，我会很高兴。

这篇小作文会介绍一下我在打 ICPC 期间学过的 LCS 相关的算法，希望能提高大家的理解。

\(\text{LCS}\) 问题：字符集为 \(\Sigma\)，你需要求两个字符串 \(A, B\) 的最长公共子序列。

1. 经典做法
2. 经典做法，小字符集
3. 排列/随机数据
4. 线性空间求解方案（Hirschberg, 1975）
5. 压位算法（Lloyd, 1985）

经典情况

经典做法：称串串长度分别为 \(n\) 与 \(m\)，复杂度为 \(O(nm)\)，与字符集无关。
令 \(f(x,y)\) 表示 \(A\) 的前 \(x\) 个字符，和 \(B\) 的前 \(y\) 个字符，产生的 \(\text{LCS}\) 长度。

\[f(x,y) = \begin{cases} f(x-1,y-1)+1, & A_x = B_y \\ \max \{ f(x-1,y), f(x,y-1) \}, & A_x \ne B_y \end{cases} \]

这个相信大家入门的时候都学过，我们这样设计状态以后，可以按顺序 \(O(1)\) 转移出答案。

---

这个问题有一个图论的刻画方法，得到的是一样的转移方程：
令网格图边权为 \(0\)，斜边为 \(1\)，问题此时变成了求左上角到右下角的最长路：
厚颜无耻地用一下 Diaosi 的图片。

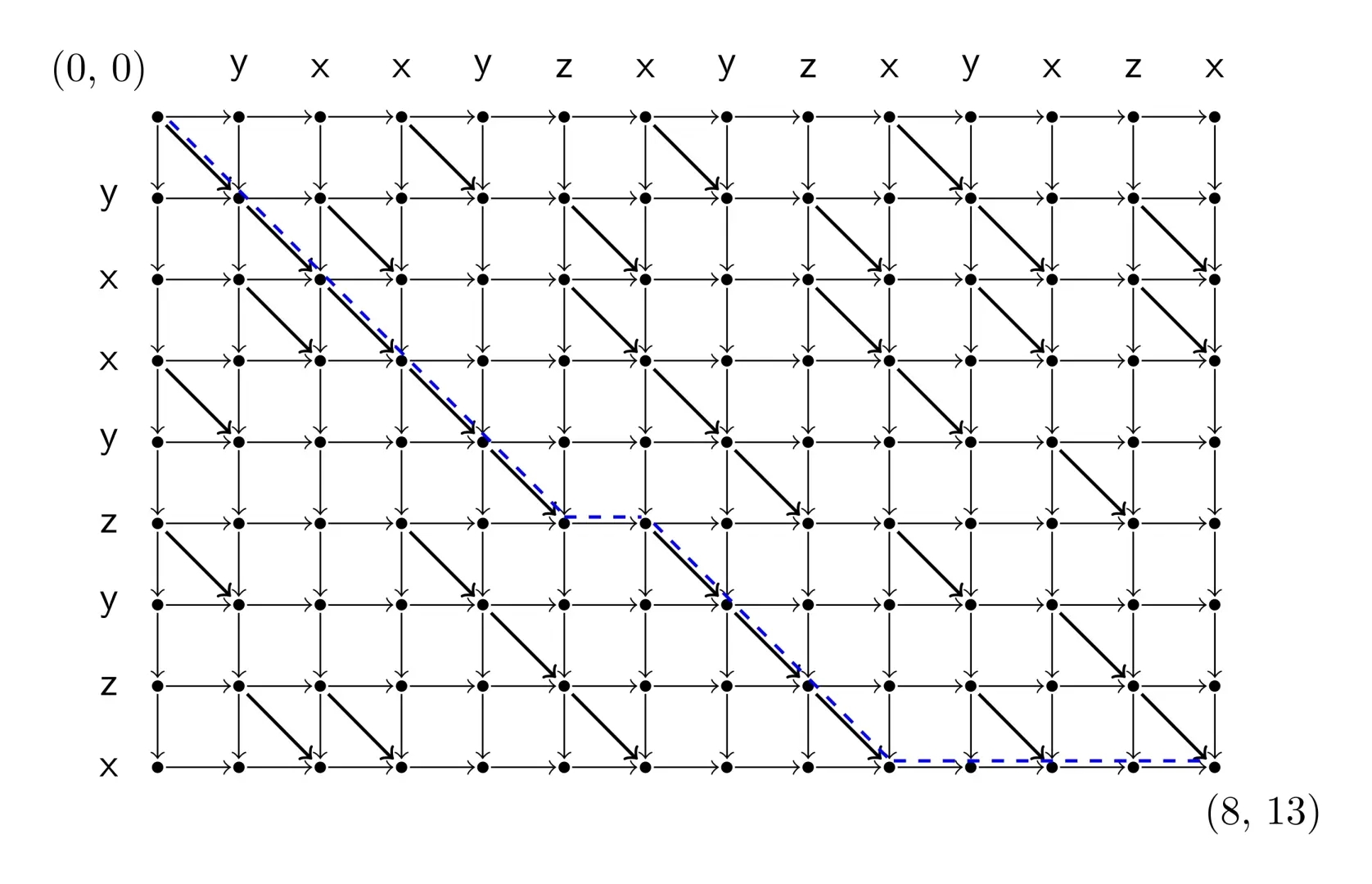
这个刻画非常有用，我们过会儿还会反复提到这个，这里先放一个例题

[HAOI2010] 最长公共子序列：

给定两个串 \(a, b\)，串长不超过 \(5000\)，请求出 LCS 的长度，以及方案数。
这里认为只要匹配的下标不同就算不同（不需要本质不同）。

Solution

长度 \(f\) 很好求，但是方案数 \(g\) 并不是非常简单，因为在 \(f\) 转移的同时累加方案数，可能在没有斜线的方格处重复计数（左上角先转移给右、下两个状态；随后右、下再转移给右下角，这样会重复多算一次）

要知道什么时候会重复计数呢？当且仅当 \(f(x,y) = f(x,y+1) = f(x+1,y) = f(x+1,y+1)\)。
这个时候可以先正常转移，累加到 \(g(x+1,y+1)\) 上面，如果多算了，就减去 \(g(x,y)\)。

从这点上看，图论刻画的一个好处就是直观；不过我们过会儿再直观，允许我先把简单的讲掉。

经典情况 2

给定长度为 \(n,m\) \((n \le 10^6, m\le 10^3)\) 的两个字符串 \(a, b\)，求 LCS，字符集比较小。
保证 \(a\) 显著比 \(b\) 长。

Solution

原始做法的状态空间为 \(f(10^6, 10^3 )=10^3\)，但注意答案到不会超过 \(m\)：

我们可以调换第一维和答案维度，得到 \(f(\text{ans}, y)=x\)，具体含义是：
一个指针指向 \(y\) ，得到 \(\text{ans}\) 的答案时，另一个指针 \(x\) 最小的位置。

我们对长串 \(a\) 预处理每个下标 \(p\) 后面最近的每种字符的下标 \(\text{nxt}(p,c)\)。

首先每个 \(f(\text{ans}, y) = p\) 的值 \(p\) 可以无条件转移给 \(f(\text{ans}, y + 1)\)。
同时状态 \(f(\text{ans} + 1, y + 1)\) 可以被转移得到 \(\text{nxt}(p,a_{y+1})\) 的值。

这样就得到了 \(O(n|\Sigma|+m^2)\) 的复杂度。

这个其实是 DP 优化的经典套路：“xxx 转最优化”，所以在这里讲这个题，主打的就是一个突兀。

经典情况 3.1

给定两个长度为 \(n (n \le 10^5)\) 的排列 \(a, b\)，求 LCS。
[ Link ]

Solution

产生一个新序列 \(C\)，其中 \(C_i\) 是数字 \(A_i\) 在 \(B\) 中的下标，E.g.

\(\text{A}=[5,1,3,4,2] \quad \text{B}=[3,1,5,4,2]\)
\(\text{C}=[ \color{#f44336} 3, \color{black} 2,1, \color{#f44336}{4,5} \color{black}] =[ 3,2, \color{#f44336}{1,4,5} \color{black}]\)

对 \(C\) 求最长上升子序列 \(\text{LIS}\) 就是答案，故时间复杂度是 \(O(n \log n)\)
同时把 \(\text{LIS}\) 视作下标（红色）在 \(A\) 中的值，恰好就是 \(\text{LCS}\) 的方案。
这里能看出两种 \(\text{LCS}\) 是 \(3,4,2\) 和 \(5,4,2\)（当然还有别的方案）

此时对 \(\text{LIS}\) 计数，能得到 \(\text{LCS}\) 的数量，建立了两者之间的联系。
但是这个 “排列” 的限制能不能放宽一点呢？

经典情况 3.2

给定长度为 \(n, m\) \((n,m\le 10^6)\) 的两个随机字符串，字符集 |\(\Sigma\)| 大于字符串长度，求 \(\text{LCS}\)。

Solution

将每个 \(B\) 中的字符出现位置列出来，并且倒序放置。

\[\begin{array}{lll} \text{A} &= [a,a,a,b,b] \quad & \text{B} &=[c,a,b,a,b,a] \\ a &= [6,4,2], \quad & b &=[5,3], \quad c = [1] \\ \end{array} \]

按 \(\text{A}\) 中的顺序把数组替换进去，其 LIS 即为答案，期望时间为 \(O(n \log n)\)
\(C=[6,4, \color{#f44336} 2, \color{black} 6, \color{#f44336} 4, \color{black}2, \color{#f44336} 6, \color{black} 4,2,5,3,5,3]\)
\(C=[6,4, \color{#f44336} 2, \color{black} 6,4,2,6,4,2,5, \color{#f44336} 3,5, \color{black}3]\)

因为排列 / 随机数据下每种字符只有常数 \(O(1)\) 个。
倒序是因为如果匹配了后面的字符，则不能回头匹配前面的字符。

4 线性空间求解方案

给定长度为 \(n, m\) \((n,m \le 5000)\) 的字符串 \(a, b\)，不限制字符集，求 LCS 的一个具体方案。
要求算法的空间是 \(O(n + m)\)。

Solution 0

Naïve 一些，我们可以在 \(O(nm^2)\) 时间内，用线性空间确定方案。

具体来说，可以进行 \(m (m \le n)\) 轮 \(O(nm)\) 的算法：

• 记录每个状态是从哪里转移过来的 / 找到行内最后的断点；
• 每次可以确定目前尾部水平的若干步，和有垂直分量的一步。

这里再放一次这个图论刻画的图片，大家理解一下。

暴力算法比较难受的地方是，因为只能使用线性空间，会导致没办法记录之前状态是从哪里转移而来的（在滚动数组的时候删掉了，只留下了最后两行之间的转移方向），这样只能知道数值，而不能直接确定方案。

Hirschberg 算法

《A linear space algorithm for computing maximal common subsequences》
作者：D. S. Hirschberg Link 原文

考虑分治，我们正常跑一次 \(\text{dp}\)，可以在 \(O(nm)\) 时间里求出中线上每个点的 \(f(·,y)\) 的值。

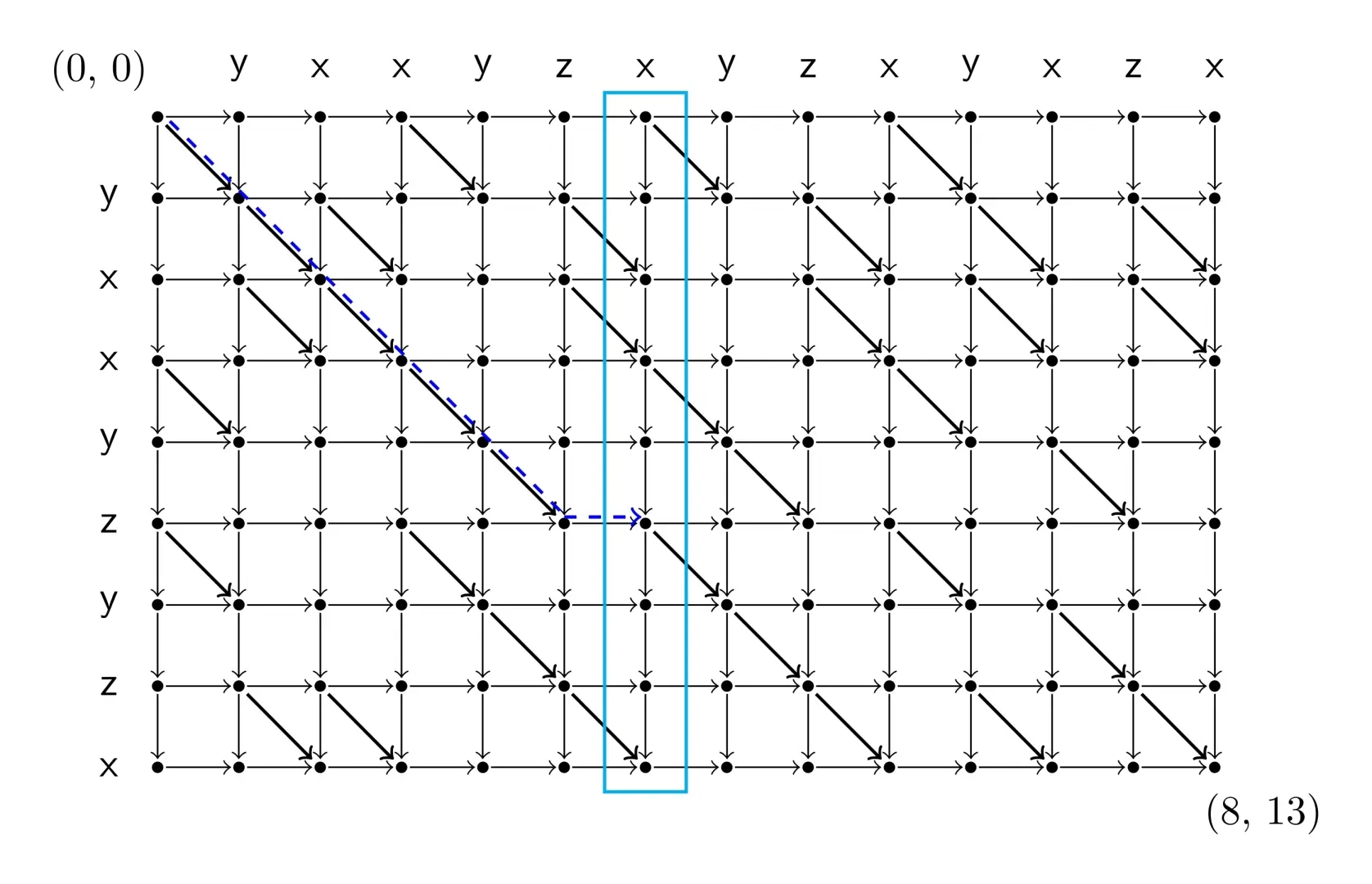
同时也可以在反图上求出中线上每个点的 \(g(·,y)\) 的值。

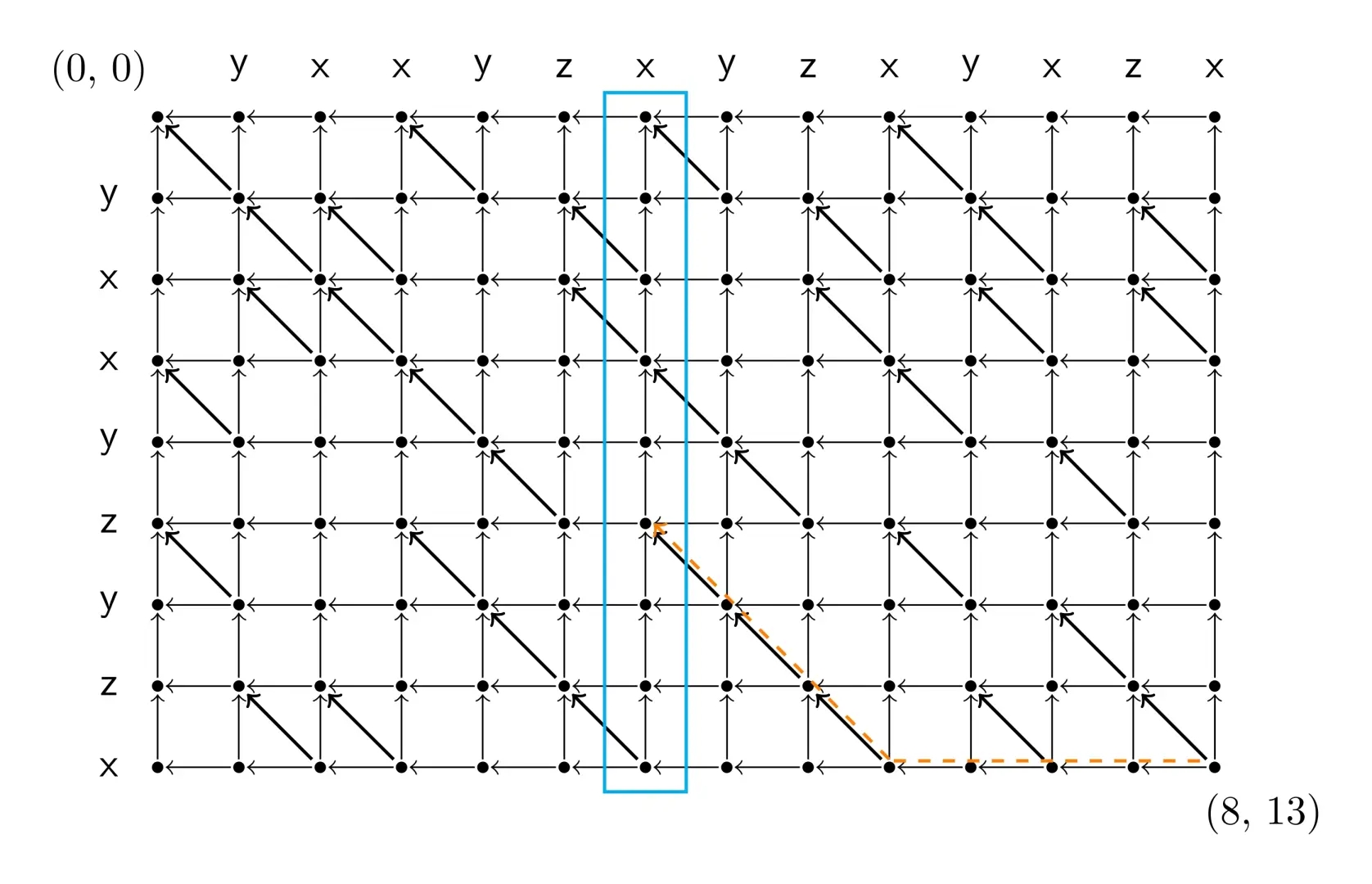
找到中线上任一最大的 \(f + g\)，可以钦定这个点在路线上，递归进两个子矩形求解路径点。

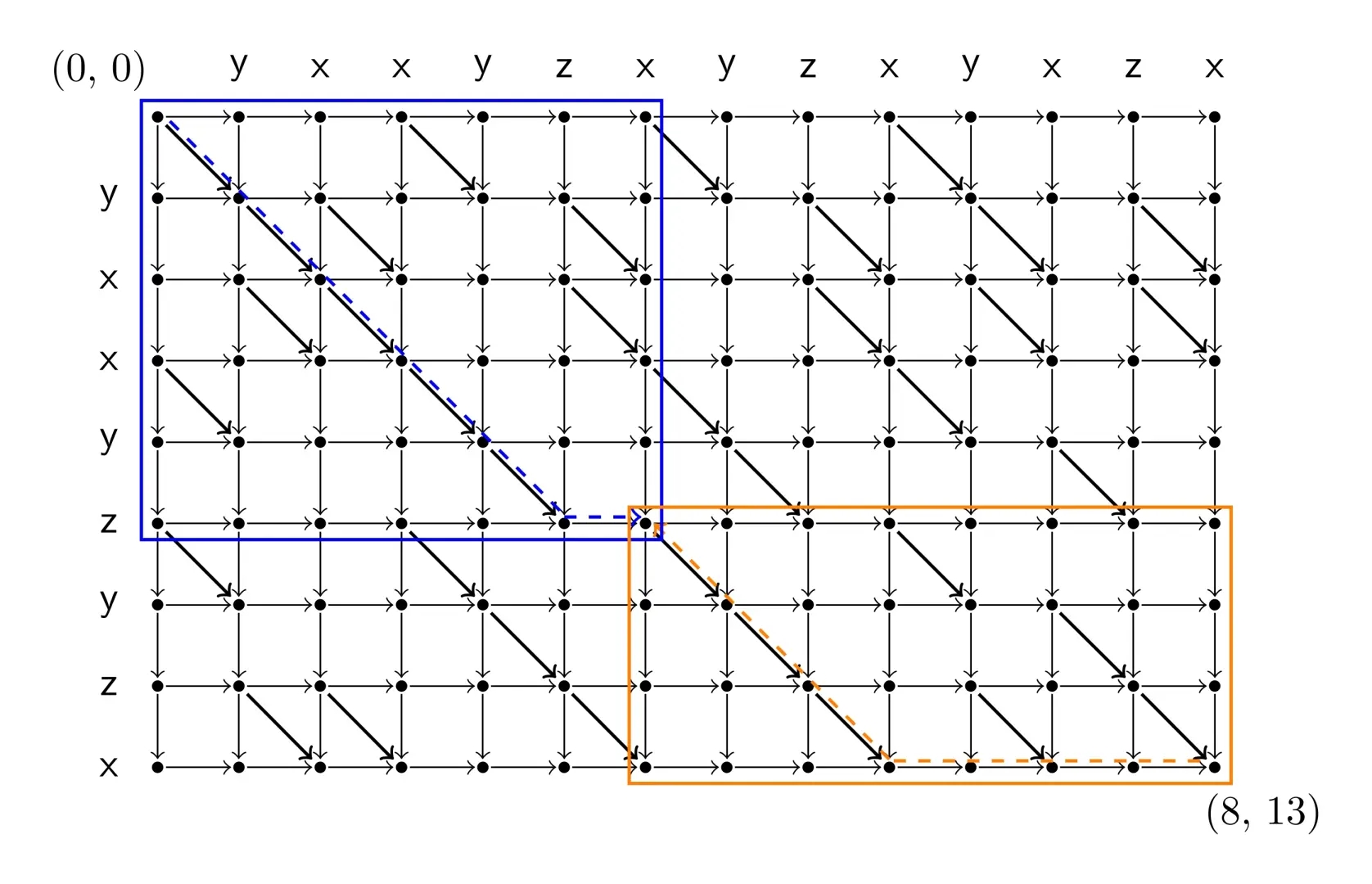
这样做以后，每层所有矩形的长度 \(n\) 减半，而所有矩形的高度之和为 \(m\)，
那么复杂度是 \(T(n) = T(n/2) + nm = \Theta(nm)\)，分析的时候其实 \(m\) 是固定值，此外算法真正的常数还要再乘一个分治的 \(2\)（这个可以考虑线段树的节点数）。

5 压位算法

给定长度为 \(n, m\) \((n,m \le 70000)\) 的字符串 \(a, b\)，任意字符集，求 LCS。
loj6564

《A BIT-STRING LONGEST-COMMON-SUBSEQUENCE ALGORITHM》
作者：Lloyd ALLISON 和 Trevor I. DIX Link 原文

这一问题可以在 \(O(nm/\omega)\) 时间内解决，我们微调一下原文顺序。主要关注算法的动机，以及具体流程。

Alphabet-strings

对于每个字符 \(c\)，用一个 \(\text{bitset}\) 表示 \(c\) 在串 \(a\) 的什么位置出现了。

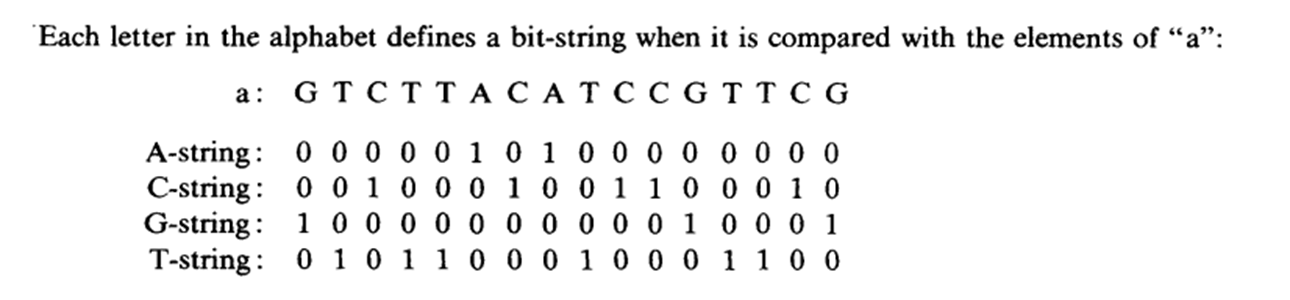
可以看出这一步空间和时间都是 \(O(|a||\Sigma|/\omega)\) 的，因为字符集大小不会比串长更大。

Matrix-M

回到最早的 \(O(nm)\) 算法，我们还有三个性质

\[\begin{cases} f(x,y) \ge f(x, y-1) \\ f(x,y) \ge f(x-1, y) \\ |f(x,y) - f(x, y-1)| \le 1 \end{cases} \]

把状态放在二维平面上，每行单调不减，且相邻之差不超过 \(1\)。
这启发我们在行内做差分（得到在行内差分的矩阵 \(M\)），而利用 \(\text{bitset.count()}\) 就可以还原答案。
形式化地，\(f(x,y) = \sum_1^k M(x, k)\)

算法流程

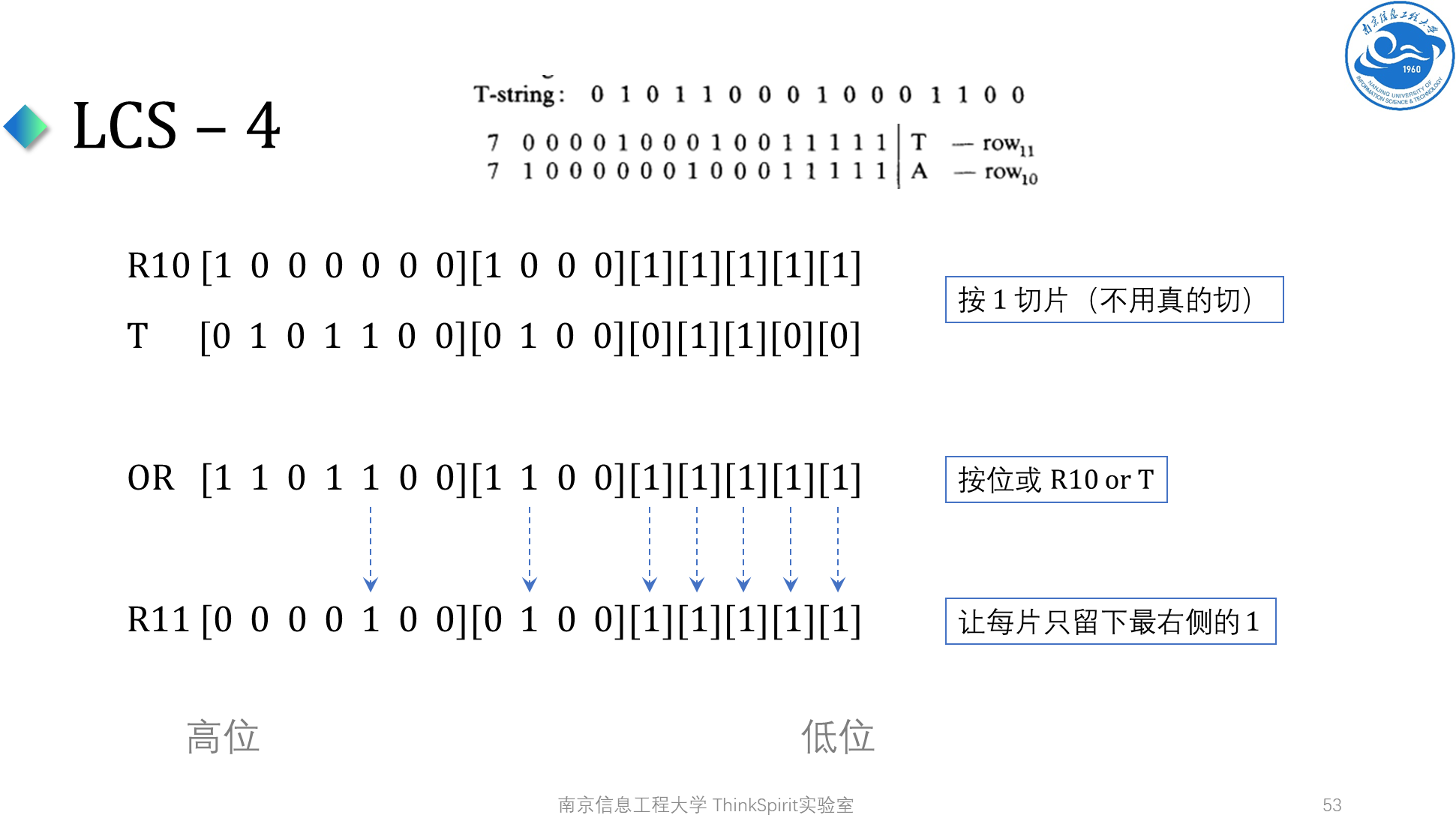
这样就做完了，最后一步可以用位运算完成，下面说明一下这个算法每一步在做什么，以及正确性

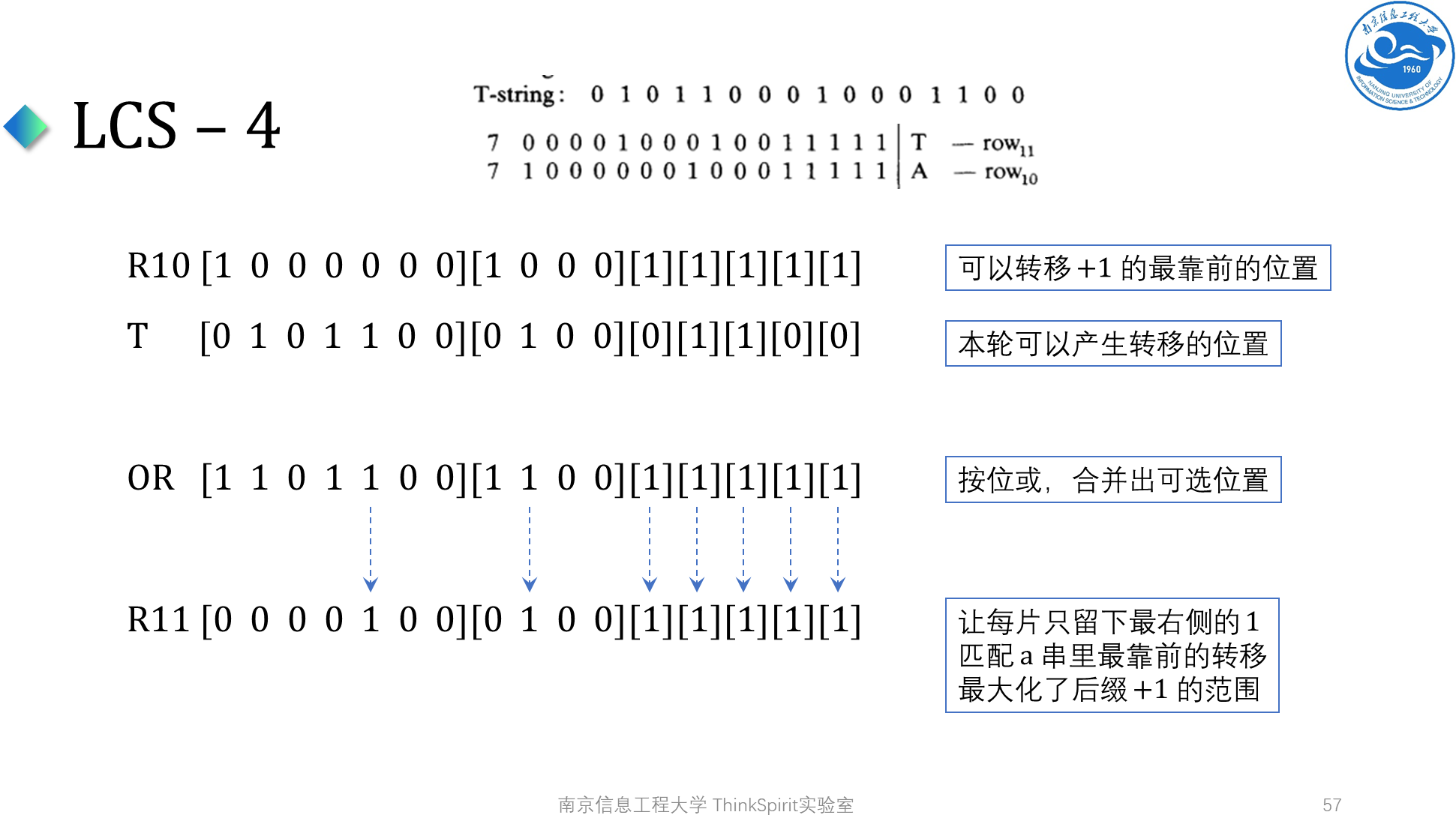
如何理解这个算法呢？大家可以考虑图论刻画，在网格图上，我们按行转移，先从上一行转移到下一行，然后在行内取前缀 max。取 max 这一步，在行内差分的情况下，本质上是最大化了后缀加一的范围，完成了上述算法的最后一步，即留下每片最靠前的 \(1\)，这个就是这个算法做的事情。

真正的小作文

我在开头说过，这个是我的退役小作文，所以我要讲一些和算法关系不大的东西，先放一下课件的图片。

我设计了很久，最后决定在左下角放一个坏女人（我在 ICPC 没打出什么成绩，还是星奏你带我奏吧）。

我想每个站在赛场上的人们，都会有那么独一无二的心愿，但真正实现愿望的人恐怕不会很多。即便如此，也正是理解了这样的真相，我才坚持到了最后，我们才真正地站在了那片黑色屏幕的森林中央。

老实说，我并没有那样的才能。但是这世上并不是用才能的好坏来决定能否成功的。
衷心希望，你能够实现你的梦想。