广义串并联图

学长 rinne 也从 ICPC 退役了，根据惯例，他也要写一篇小作文（点头）

---

2019 年，吴作同在集训队论文《公园》命题报告中正式引入了这个结构。在这种特殊图上，存在一组收缩操作，存在一类 DP 方法。具体的正确性证明可以在集训队论文里找到，这里暂略。我们非常 naïve 地介绍一下这个特殊图，以及所谓的 “广义串并联图” 算法。

前置知识

因为网上 OIer 的资料（除了论文原文）基本都出现了一个错误的描述，我们先介绍一些概念：

细分操作：在某条边上，新增一个二度点。这个操作 不改变 原图顶点度数。

细分图：若 \(G_2\) 可以从 \(G_1\) 通过若干次细分操作得到，则 \(G_2\) 是 \(G_1\) 的细分图。

同胚：如果两张图 \(G_1, G_2\) 分别存在细分图，满足 \(G_1’ = G_2’\)，那么 \(G_1\) 和 \(G_2\) 同胚。

不难看出，利用细分操作，可以定义出一定的拓扑关系。

---

广义串并联图
对于任意 \(4\) 个节点，都不存在 \(6\) 条两两没有公共边的路径连接这个节点中的每一对节点。

错的：如果无向图 \(G\) 上不存在同胚于 \(K_4\)（四个点的完全图） 的子图，那么图 \(G\) 是广义串并联图。
这个广泛网传的说法是必要不充分的，过会儿会讲一下。

下面这俩不是广义串并联图（暂时不容易用肉眼快速判断）：

一些常用性质：

• 如果无重边，满足 \(m \le 2n\)，且是平面图（但平面图不一定是广义串并联图）
• 通过收缩\(^\dagger\)操作，最后会剩下一个点（充要，可以作为广义串并联图的判定手段）

\(\dagger \quad\) 收缩操作（由三个子操作组成，没有顺序要求）：

• 删 1 度点（Rake）：删除一个 1 度点（和一条边）
• 缩 2 度点（Compress）：删除一个 2 度点（将它两侧的点用一条新边连接，即细分的逆操作）
• 叠合重边：把多条重边合成为一条边

---

这里用第二个性质，即通过收缩\(^\dagger\)操作，最后会剩下一个点，来判断一下前面两个图是不是广义串并联图。
所以第一个图不是广义串并联图（只能进行 \(4\) 次缩二度点的操作，最后无法收缩成一个点）

值得注意的是，这个图并不同胚于 \(K_4\)，广泛网传的说法看来并不充要。
而前面那个三角形的图，也不是广义串并联图（它就没办法进行收缩操作）。

具体应用

我们利用下面一些题目，介绍一下怎么利用这个算法进行 DP。有一些题目，尤其是仙人掌上的，是可以在圆方树上 DP 的。这类 “广义串并联图” 技巧是更加通用的算法，可能有额外的代价。

[SNOI2020] 生成树

给定带标号无向连通图 \(G\)，已知 \(G\) 在删掉一条边后是一颗仙人掌。求 \(G\) 的生成树个数。
（仙人掌：不存在两个拥有公共边的简单环的无向连通图）
\(n \le m \le 2 \times 10^5\)

首先可以说明这个图是广义串并联图：仙人掌 \(4\) 个点之间最多有 \(4\) 条不交路径，再加一条边不超过 \(5\) 条。我们介绍一下怎么在这种图上，利用 “收缩” 操作进行 DP。

对每条边 \(e\) 设置 \(f(e)\) 表示，只考虑 \(e\) 这个结构，使 \((u, v)\) 连通的方案数。
类似地， 再设置 \(g(e)\) 表示，只考虑 \(e\) 这个结构，使 \((u, v)\) 不连通的方案数。
这个 \(g\) 可能比较反直觉，但是我们过会儿就知道为什么这么设置状态了。

根据定义，初始 \(f(e) = g(e) = 1\)，再设置 \(ans = 1\)。
然后我们加上收缩操作：删 1 度点 / 缩 2 度点 / 叠合重边。

删 1 度点（消去串联结构）
对于 $1$ 度点，那么它在结构上的地位可以类比成叶子。 如果和外部不连通，一定无法构成生成树，故必须连通。我们直接 $ans=ans \times 𝑓_𝑒$ 然后删掉这个点和边。E.g. 一条链/树。

叠合重边（消去并联结构）

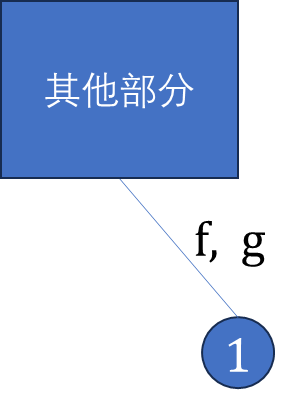
• \(f=f_1⋅g_2+f_2⋅g_1\)，这里没有 \(f_1⋅f_2\)，否则不是生成树了。
• \(g=g_1⋅g_2\)。

可以看出设计 \(g\) 的原因，重边是并联结构（环），断边才能产生生成树。

缩 2 度点（消去串联结构）

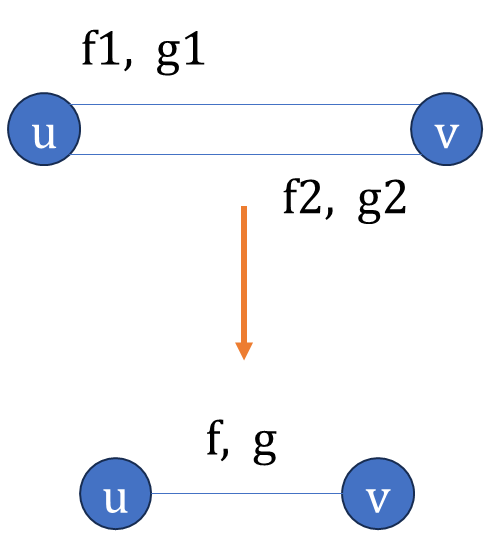
• \(f=f_1⋅f_2\)，因为要使 \(u, v\) 连通。
• \(g=g_1⋅f_2+g_2⋅f_1\)，没有 \(g_1⋅g_2\)，不然会裂开。

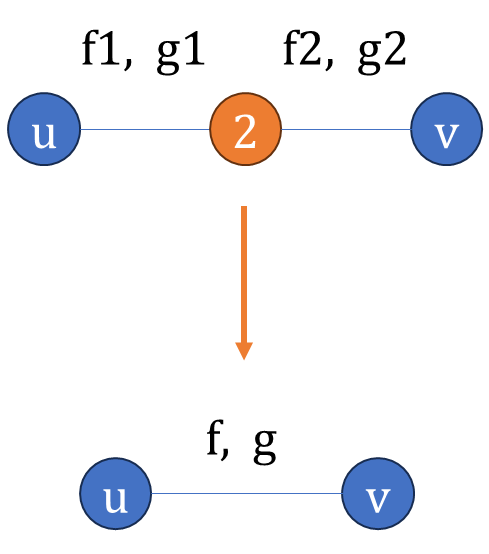
可以证明这么做，把图删到只剩一个点的时候，\(\text{ans}\) 即为答案。可以理解为，在广义串并联图上，收缩操作给出了一个正确的通用 DP 顺序，因为这个图很特殊，只要转移方程对了，答案就是对的。

实际上，在开始收缩以后，每条边是原图的一个 “结构”，而非一条边。 我们只要保证 “结构” 之间的转移是正确的，答案就是正确的。 三种操作没有顺序要求，在实现时只需要用类似拓扑排序的做法。 因为是无向边，所以我们要支持对正反边进行修改（用 map 存图），下面是我板子里的加边，拓扑的部分很好写我就不放了，大家去看别人的代码也一样 233。

using info = pair<int, int>; // DP 维护的信息
map<int, info> G[maxn];

void add(int u, int v, int f1, int g1) {
  if (G[u].count(v)) {  // 有重边
    auto [f2, g2] = G[u][v];
    auto f = (f1 * g2 % M + f2 * g1 % M) % M;
    auto g = g1 * g2 % M;
    G[u][v] = G[v][u] = info(f, g);
    return;
  }

  G[u][v] = G[v][u] = info(f1, g1);
}

QOJ856 Cactus

给定一棵仙人掌，用 \(k\) 种颜色给每个结点染色，满足相邻的结点颜色不同，求方案数，对大质数取模。
\(n \le m \le 4 \times 10^5, k \le 10^9\)

我们尝试仿照前面的做法，考虑设 \(f\) 表示两端颜色一样的方案数，\(g\) 为不同的。
在叠合重边时 \(f=f1⋅f2 / k\) 即对每个 \(f\) 先除以 \(k\)（钦定两端变成 \(1\)），然后再乘 \(k\) 复原数量。
这个时候 \(g\) 就更加麻烦，这里介绍一个技巧，直接提前钦定颜色，在转移的时候把种类数乘回去。

钦定：点 \(u\) 总是颜色 \(1\)，这样最后乘 \(k\) 就是答案（对所有颜色循环位移）。

• 用 \(f\) 表示确定两端颜色一样的方案数，因此这里表示 \(u, v\) 都是 \(1\) 颜色;
• 用 \(g\) 表示两端不同的方案数，且两端必须染 \(1\) 和 \(2\);
  在过程中乘 \(k-1\)，可以让 \([2, n]\) 的颜色循环位移。
• 初始 \(f = 0, g = 1, \text{ans} = k\)

这样我们就可以列出转移方程，大家可以暂停阅读，手玩一下，比较趣味生煎的：

• 叠合重边：
  \(f = f_1⋅f_2\)
  \(g = g_1⋅g_2\)
• 删 1 度点：\(\text{ans} = \text{ans}⋅(f+(k−1)g)\)
• 缩 2 度点：
  \(f = f_1⋅f_2+ g_1⋅g_2(k-1)\)
  \(g=f_1⋅g_2+f_2⋅g_1+g_1⋅g_2(k−2)\)

这样就比较取巧地做完了，这个钦定的手法应该不是特别东雪莲，值得学习，同时还避免了除法操作。

习题 1

给定一个广义串并联图，你要给边定向，求产生 DAG 的方案数。
\(n \le m \le 4 \cdot 10^5\)

Hint

让 $f$ 表示只通过这个结构，$u→v$ 的方案数（视为有向边）。

让 \(g\) 表示只通过这个结构，\(u↛v\) 且 \(v↛u\) 的方案数。

初始 \(f=1, g=0, \text{ans}=1\)。

此外还能观察到（同一条无向边）正反边的 \(f\) 其实数值是一样的。

Solution

• 叠合重边：
  \(f =f_1 · g_2+f_2 · g_1+f_1 · f_2\)
  \(g=g_1 · g_2\)
• 删 1 度点：
  \(\text{ans} = \text{ans}⋅(2f+g)\)
• 缩 2 度点：
  \(f =f_1·f_2\)
  \(g=2f_1·g_2+2f_2·g_1+2f_1·f_2+g_1·g_2\)

小结

如果这张图已经是广义串并联图，简单的情形是利用边来完成 \(\text{dp}\)。 主要使用的操作有三种：删 1 度点 / 缩 2 度点 / 叠合重边。在把图收缩成一个点后，就完成了 \(\text{dp}\) 的过程。这个 \(\text{dp}\) 的过程可能无法直接设和答案一样形式的状态。因为有三种非常不寻常的收缩操作，要支持的是 “结构” 之间的转移。

稍微一般的情形

接下来我们介绍一类放宽的问题，连通图满足 \(m \le n+k\) 而 \(k\) 较小。

考察收缩的三种操作，均不会使操作后的 \(m - n\) 变大，依然满足 \(m \le n+k\)。
收缩完成后，点的度数都至少是 \(3\)，所以还满足 \(2m \ge 3n\)。联立两个式子，可以得到一个不等式组，对应的含义是，最后无法操作时，会留下来一个 \(n \le 2k, m \le 3k\) 的结构。只要额外对这种结构做一些计算（此时边权是新的 \(f, g\)）。

abc419_g :: Count Simple Paths 2

给定数据范围很特殊的无向连通图。求出从 \(1\) 走到 \(n\) 恰好走了 $ 1, 2 \dots n - 1$ 条边的 简单路径 数量。
\(n,m\le 10^5, m-n \le 20\)

想一下，其实是一棵树加了很少的边，那么中间很多链是可以缩成一条边的。

• 删 1 度点：因为必须是简单路径，可以直接删除一度点，因为走不进去。
  注意如果顶点是 \(1\) 和 \(n\)，这个时候不删，直接跳过。
• 叠合重边：不叠。
• 缩 2 度点：考虑二度点的形态，完全可以缩边，直接合成大边权！
  特别地，如果 \(u \to v \to u\) 可以直接删掉（除非 \(v\) 是 \(1\) 和 \(n\) 则不要删）。

最后会剩下来至多 \(40\) 个点 \(60\) 条边，爆搜一下 \(1\) 到 \(n\) 的所有路径。这个做法其实等价于建了一颗虚树。

为什么复杂度是对的呢，因为本质不同的 \(S\) 到 \(T\) 的简单路径数量至多为 \(2^{m-n+1}\)。

真 · 广义串并联图

哈哈，广义串并联图是图的性质，而 “广义串并联图方法” 才用来代指那种 DP。
下面这些题目里，我们使用广义串并联图的性质，而不是什么传奇地痞算法。

广为人知题

给你一个 广义串并联图，用 \(3\) 种颜色给点染色，使得相邻顶点不同色。输出一个构造方案。
\(n,m \le 10^5\)

我们先把图合并成一个点，然后把合成顺序反过来，倒着染色即可。如果数据范围是 \(m-n \le k\) 的那种，先合并串并联图，后得到一个子图，可以先爆搜子图的答案，然后就能倒着染色了。

这样做是对的，是因为我们只能新增 \(1\) 或 \(2\) 度点，一定可以用第三种颜色做到合法。

爆搜有 \(O(1.33^{n})\) 的算法 [ link ]，但是我读了一下，感觉比较原神，完全根本压根不推荐大家读这个。

[JOI Open 2022] 放学路

给定 正边权 的无向图，问是否存一条 \(1\to n\) 的简单路径 \(S\)，满足 \(S\) 的长度和 \(1 \to n\) 的最短路不一样。
只要判断是否有解。

\(n,m \le 2 \cdot 10^5\)

这个题非常妙，部分分的提示非常关键，所以如果丢进 XCPC 恐怕就是深水炸弹了，可惜它已经问世了。第三个子任务：\(m - n \le 13\)。

Hint

首先我们假设整张图点双联通（或者说，去掉和 $1,n$ 路径完全无关的点）

手玩发现，如果出现了 “对于 \(4\) 个节点，存在 \(6\) 条两两没有公共边的路径连接这个节点中的每一对节点” 的结构，那么一定存在答案，因为是正边权，就算最短路经过其中，绕一下一定可以走出非最短路。就是说如果这个图不是广义串并联图，那么输出有解。

那么如何只考虑那些与 \(1,n\) 路径有关的点呢？
我们直接加一条 \((1,n,w)\) 其中 \(w\) 是最短路长度的边，这样如果有关，一定同时和 \(1,n\) 在同一个点双里。

现在现在只需要考虑是广义串并联图的情形。

Solution

进行 “收缩” 操作：

• 叠合重边：边权一样则变成一条边，不同则合成一条 \(-1\) 的边，表示有解。
• 删 1 度点：不要删 \(1\) 和 \(n\)，其他点可以直接删掉。
• 缩 2 度点：两条边边权相加。

这样最后一定只会剩下一条边 \((1, n)\)，这个时候考察这条边的权值，如果是 \(-1\) 则有解，否则无解。

[CCPC 2023 北京市赛] 最小环

给定一张特殊的有向图，边权为正。你要求出图上的最小环大小。保证图弱连通。
\(n,m \le 3 \cdot 10^5, m-n\le 1500\)

看到数据范围，有点熟悉，但是有点陌生。

类似前面几个题的做法，不过这个题是有向图，所以略有不同：

• 叠合重边：保留一条最小权的边。
• 删 1 度点：入度为 1 或者出度为 1 可以直接删掉，因为不在环上。
• 缩 2 度点（缩入度为 1 且出度为 1 的点）：边权相加。
  注意如果是 \(u\to v \to u\) 就不缩，防止出现自环。

处理完以后我们发现图的规模变成了 \(O(k)\)，\(k\le 1500\) 的，这样可以直接暴力了。
枚举环上的点 \(x\)，然后在正反图上分别跑最短路，暴力计算答案。

一些习题

BZOJ4316 小 C 的独立集

给定一个仙人掌 \(G\)，求 \(G\) 的最大独立集 \(T\) 的大小。独立集的意思是 \(G\) 的导出子图 \(T\) 里没有边。
\(n,m\le 10^5\)

本题的转移是 \(\max\) 的结构，而非计数，故不容易在删一度点的时候统计答案。对于这种情况，我们尝试对点也设置一些状态（因为最后剩下一个点），尝试在转移的时候更新边和点的 \(\text{dp}\) 状态，把答案挂给最后一个点。

对顶点维护 \(g_u(01)\) 表示 \(u\) 是否被选入时的答案。维护 \(f_e(01, 01)\) 表示两端点是否被选入，且不考虑 \(u, v\) 的贡献的答案。因为储存时是有向边，所以可以钦定两个维度依次对应从 \(u\) 指向 \(v\)。
初始 \(g_u(1) = 1\)，以及 \(f_e(1, 1) = – \text{INF}\)，其他状态都是 \(0\)。

• 叠合重边：
  四个状态 \(f_e (x,y)=f1(x,y)+f2(x,y)\)
• 缩 2 度点：枚举二度点的状态 \(y=01\)
  \(f_e (x,z)=f1(y,𝑥)+g_u (y)+f2(y,z)\)
  注意这里的状态位置，因为这两条边是 \(u\) 为起点的。
• 删 1 度点：
  设删除了 \(u\) (其连向 \(v\))，\(\text{chmax}(g_v(t), g_u(t\text{ ^ }1)+f_e (t\text{ ^ }1,t))⁡\) 这样能把边的贡献挂到点上。

本题细节是注意在更新每条边时，正确更新其反边的值。
对最后一个点的两个状态取 \(\max\)，这样就解决了这个题。

[HNOI/AHOI2018] 毒瘤

给定一个特殊的连通图 \(G\)，求 \(G\) 的最大独立集 \(T\) 的大小。
\(n,m\le10^5,m-n\le 10\)

在前面那个题基础上，最后会剩下来至多 \(2k\) 个点，\(3k\) 条边，我们 \(2^{2k}\) 枚举每个点选了没有，然后暴力 \(\text{check}\) 计算答案。注意存在更加好的做法。

「2019 集训队互测 Day 3」公园

论文原题。

给你一个广义串并联图，你要给点黑白染色。点 \(x\) 染成黑色会有 \(w_x\) 贡献，白色则为 \(s_x\) 贡献。
对于边 \(e\)，如果两端点颜色一样，有 \(c_e\) 贡献，不同则有 \(d_e\) 贡献。
有 \(q\) 次修改，每次改一个贡献的值，求可以得到的最大贡献。

\(n,m,q \le 10^5\)

先不带修，对每条边维护 \(f_e(01, 01)\) 表示选了没有。我们记录收缩的转移过程，得到的是一棵二叉树（因为操作的点度数不超过 2）。在这个树上做动态 dp 即可，具体做法可以参考 P4719。

CF2164F2 Chain Prefix Rank

给定一棵根为 \(1\) 的树，以及序列 \(a\)，求有多少排列 \(p\) 满足：

• 点 \(u\) 恰好有 \(a_u\) 个祖先 \(v\)，满足 \(p_v \lt p_u\)

\(n \le 5 \cdot 10^5\)

玩一下一条链的情况，我们发现如果从上到下确定，其实是能确定每个点的 rank 的（知道头上的前驱和后继是哪个点）。我们可以根据大小关系建出一个 DAG：

• 我们加入点 \(x\) 时，找到头上的前驱 \(p\) 和后继 \(s\)，连 \(p \to x \to s\)。
  比较巧妙的是，这样得到的是一个广义串并联图，这里借用 xujindong_ 的图（和题解的思路）。

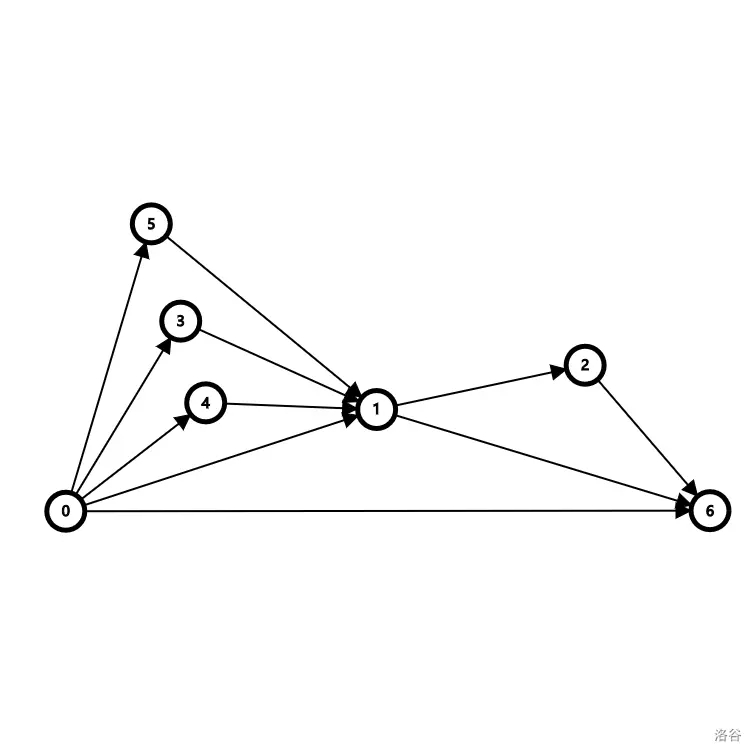
方便起见，我们在原始树根的头上再加两个点 \(1 \to 0 \to n+1\)，强制这两个点必须是最大和最小，这样不影响答案。建出这张 DAG 图后，从下面开始往上合并，将上面的两条边和最下面的一条边合并，三个点分别叫 \(u \to p \to v\)。设 \(f\) 表示这条边的方案数，\(g\) 表示这条边上的点数（不含端点）。

点数的转移是简单的 \(g'_{u,v} = g_{u,v} + g_{u,p} + g_{p,v} + 1\)，加起来就行。
然后计算方案数 \(f'_{u,v} = f_{u,v} \cdot f_{u,p} \cdot f_{p,v} \cdot \binom{ g'_{u,v} }{ g_{u,v} }\)，因为并联结构可以随便插入而不影响相对大小。