Advanced Algorithm —— LP Rounding

https://tcs.nju.edu.cn/slides/aa2025/LPRounding.pdf

Unrelated Machine Scheduling

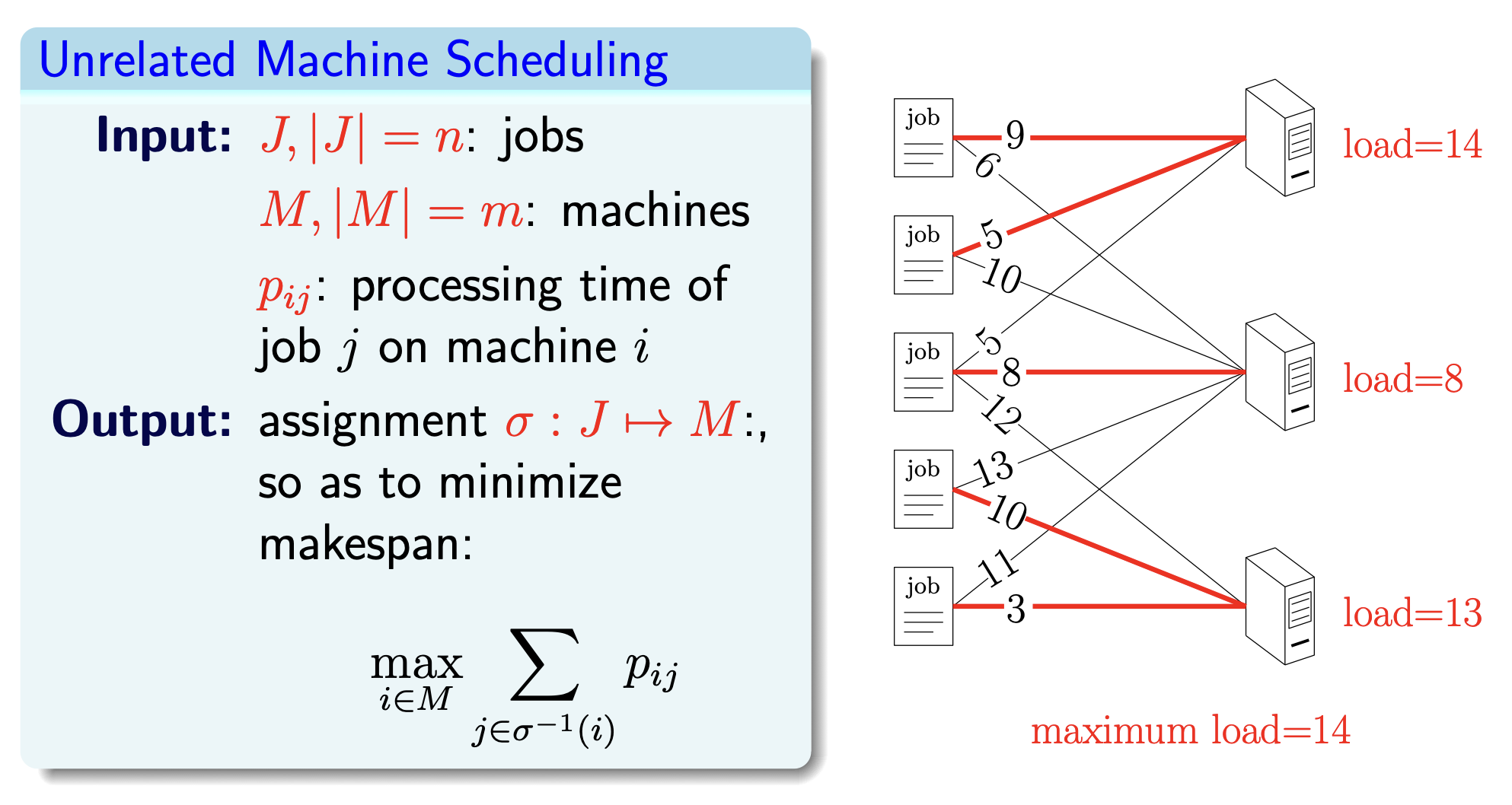
转化为判定形式，判定所有机器的 load 能否均不超过 \(T\)

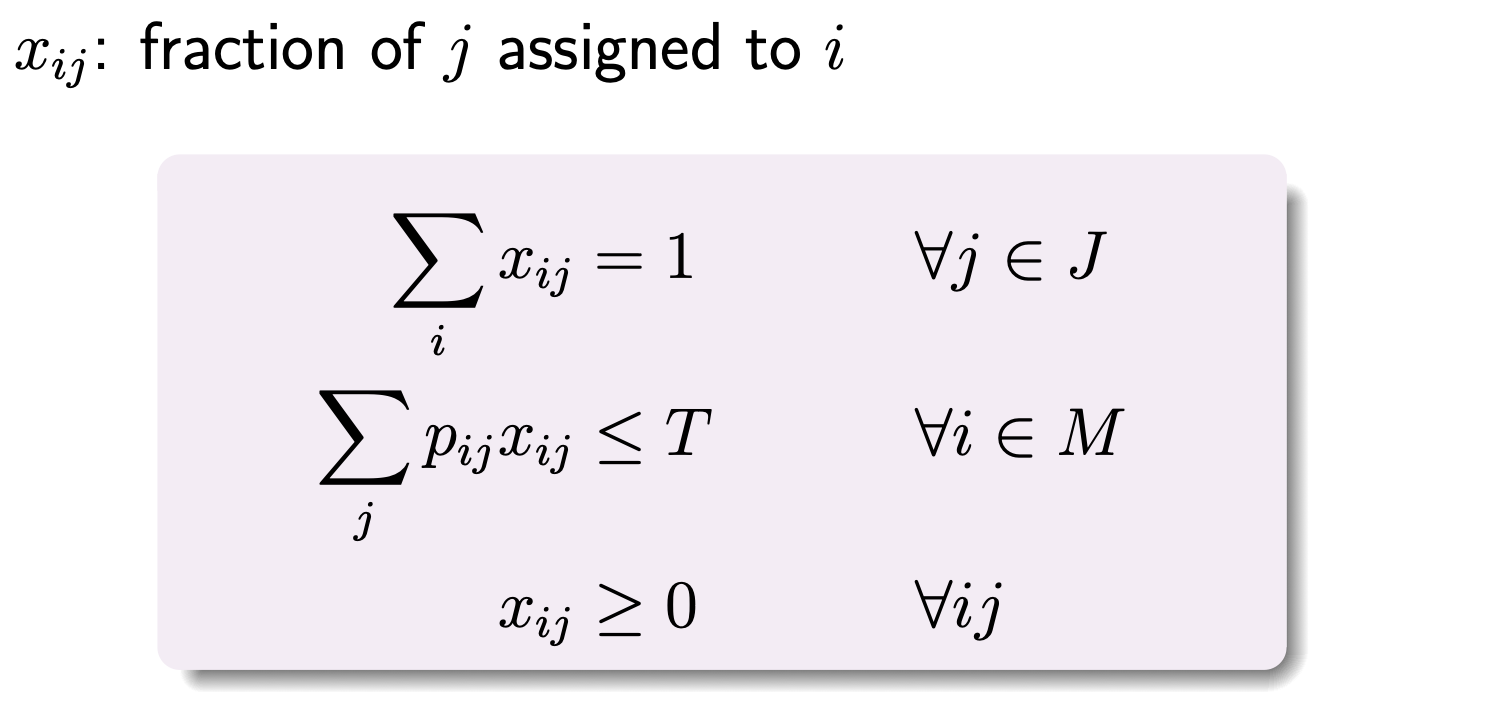
一个问题是 integrality gap 可能会非常大，如 1 个任务，\(n\) 个机器，在每个机器时间上都是 1。整数最优解是分给任意一个机器，是 1。但 LP 会均分这个任务，最优解为 \(1/n\)。这样 integrality gap 是 \(n\)。

为了解决这个问题，当 \(p_{ij} > T\) 时，令 \(x_{ij}\) 必须为 0，这样就需要令 \(T\) 为二分的常数，不能为 LP 的变量。

fix 一个机器 \(i\)，将 \(x_{ij}>0\) 的任务 \(j\) 按照 \(p_{ij}\) 降序排列，分别建一个 sub-machine，令每个 sub-machine 承担不超过 1 的 fraction（按照顺序分配即可，只有每个机器的最后一个 sub-machine 拥有的 fraction 可能小于 1，其余均为 1）。

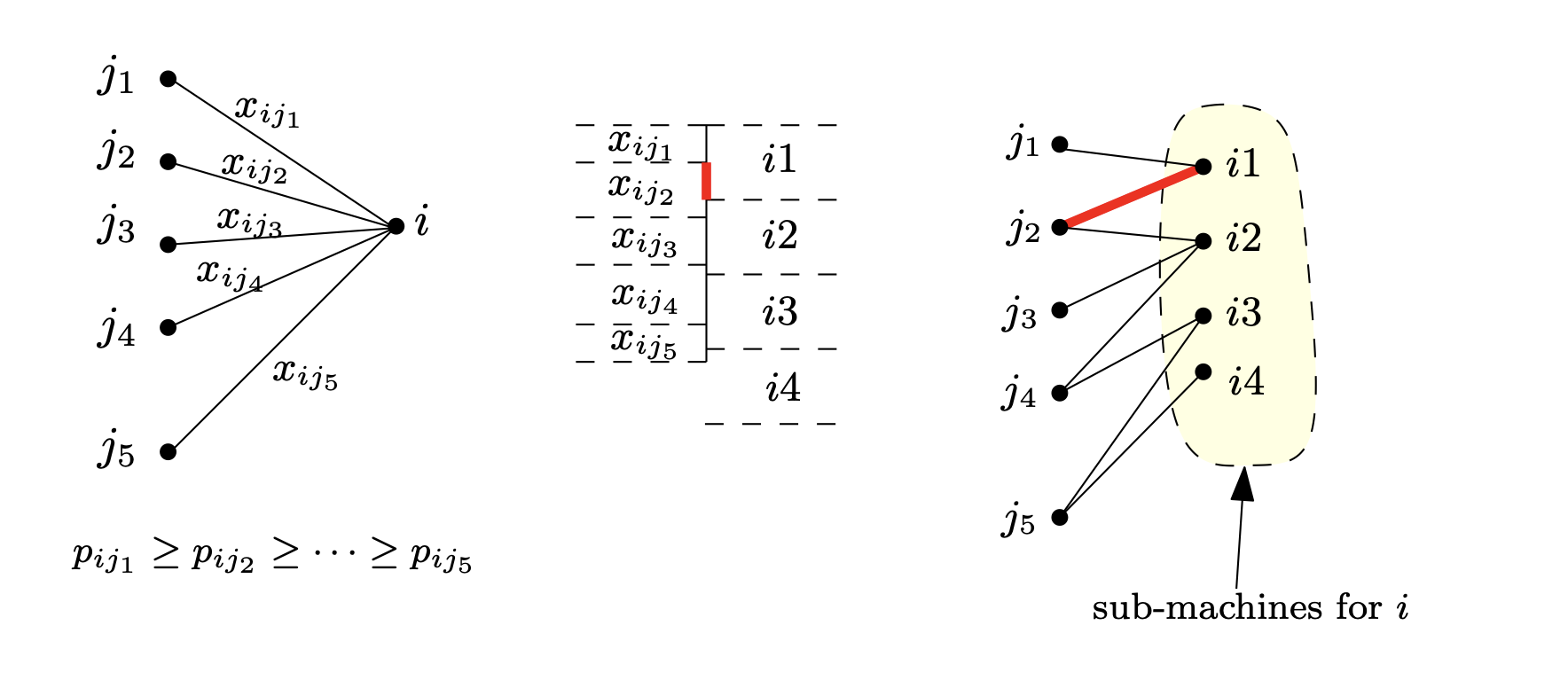
之后这对应了二分图匹配的 LP （即每个点 \(v\) 有一个 constraint 为 \(\sum_{u} x_{uv}\le 1\)），直接进行一个二分图匹配，让每个任务都匹配一个 sub-machine。

这样最坏的情况，就是对于一个 设施的每一个 sub-machine 都分到了连接到该设施的第一个任务（因为从大到小排序了）

就是凑一下系数可以发现近似比为 2。另外这个 2 也是 integrality gap，考虑 \(n+1\) 个任务分到 \(n\) 个机器，所有时间都是 1。这样整数解必然有一个机器运行两个任务，时间为 2。而 LP 可以让每个机器运行 \(1+1/n\) 个任务。所以 integrality gap 为 \(2/(1+1/n)\approx 2\)。

Congestion Minimization

\(k\) 对源汇，每对需要 1 单位流量。最小化流量最大的边的流量。

源点均为 \(s\)，汇点均为 \(t\)：令每条边容量为 1，求 s 到 t 的最大流 \(L\)，答案为 \(\lceil k/L\rceil\)。
源点均为 \(s\)，汇点不同：二分，判定 \(c\) 是否可行。建立超级汇点，每个汇点向超级汇连容量为 1 的边。每条边容量为 \(c\)，从 \(s\) 出发 \(k\) 的流量，cehck 是否都能到超级汇。
源汇均不同的话无法用上面的做法，因为这样会丢失点对关系，无法保证从 \(s_i\) 出发的流量到达 \(t_i\)。

\(C\) 表示最大拥塞，有一个 typo，左边的 LP 的第二个限制应为对所有 \(e\) 均有 \(\sum_{i,P\in \mathcal P_i,e\in P} x_P \le C\)。

左边是一个指数级变量个的 LP，\(s_i\) 到 \(t_i\) 之间的每条路径 P 之间有一个变量 \(x_P\)，表示这个路径的 fraction。右边的 LP 和左边等价，就是将路径的 fraction 放到了每条边上，可以通过逐渐求增广路的方式转化为左边的 LP。

具体算法为：

根据上面的算法，一条边的期望拥塞为 \(\sum_{i,P\in \mathcal P_i,e\in P} x_P\) 是不超过 \(C\) 的。

用 chernoff bound，限制每条边的拥塞超过 \((1+\delta)C\) 的概率不超过 \(\frac{1}{2n^2}\) 这样通过 union bound 可以 w.h.p 保证 ratio 为 \(\delta\)。

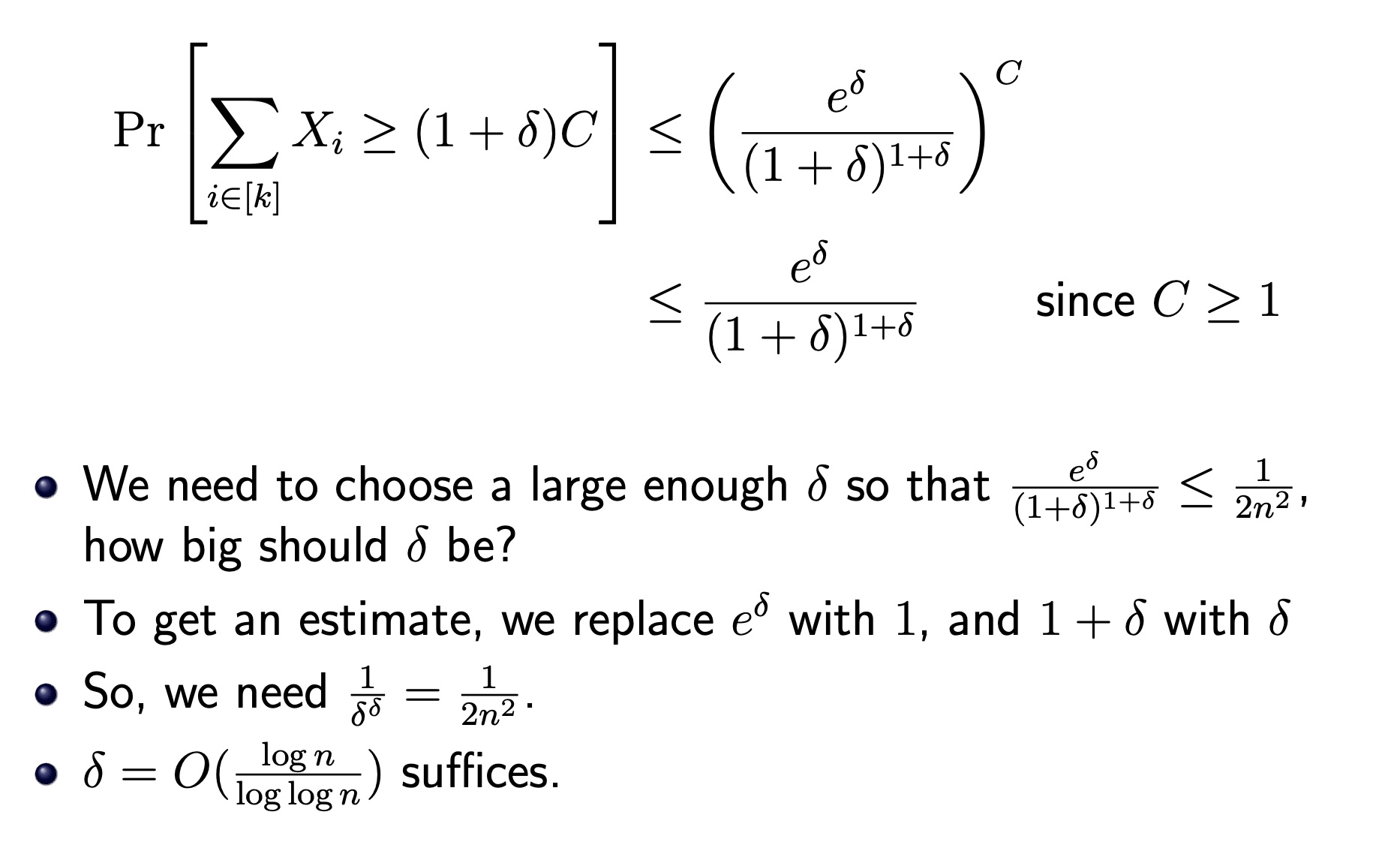
因为这里令 \(\delta \rightarrow \infty\) ，所以 chernoff bound 中的界 \(\frac{e^\delta}{(1+\delta)^{1+\delta}} \approx \frac{e^\delta}{\delta^\delta} = O(\frac{1}{\delta^\delta})\)。