Lagrangian Relaxation for the k-Median Problem: New Insights and Continuity Properties
https://people.orie.cornell.edu/shmoys/pdf/kmedian-esa.pdf
这篇文章是对于 JV algorithm 的改进。JV 对于 facility location 问题可以得到一个 3-approx 的 LMP。根据 facility location 和 k-median 的转化关系,如果存在 \(z\) 使得 JV 对于 \(z\) 为设施开放成本的 facility location 能够输出一个开放 \(k\) 个设施的解,那么就对于 k-median 也得到了一个 3-approx。但遗憾的是,JV 随着 \(z\) 的变化,开放的设施数量并不是连续的,所以如果使用 JV 来解 k-median 可能需要选择参数 \(z_1,z_2\) 得到两个解 \(\mathcal S_1,\mathcal S_2\) 满足 \(|\mathcal S_1|\le k \le |\mathcal S_2|\),即一个 3-approx 的 bi-point solution,而从 bi-point solution 转化到整数解会再损失一个 2,所以最终是 6-approx 的。
本文修改 JV 使得其具有了连续性的性质,但是本文的需要求最大独立集,所以不是多项式复杂度的。(与之对比,JV 只需要求一个极大独立集,JV 具体流程可以看这一篇博客)所以得到了一个只基于线性规划的 3-approx 的算法,这说明了 k-median 的 LP 的 integrality-gap 不会超过 3,即 \(opt/LP\le 3\)。(如果存在一个 instance 满足 \(opt> 3LP\),那么算法给出一个成本不超过 \(3LP<opt\) 的解,矛盾)
那为什么存在一些 k-median 的算法的近似比小于 3,不能说明 integrality-gap 的上界更小呢?因为这些算法并不是完全基于 LP 的,如这篇 \(1+\sqrt3\) 的文章。考虑下面这个经典的 gap 2 的情况。
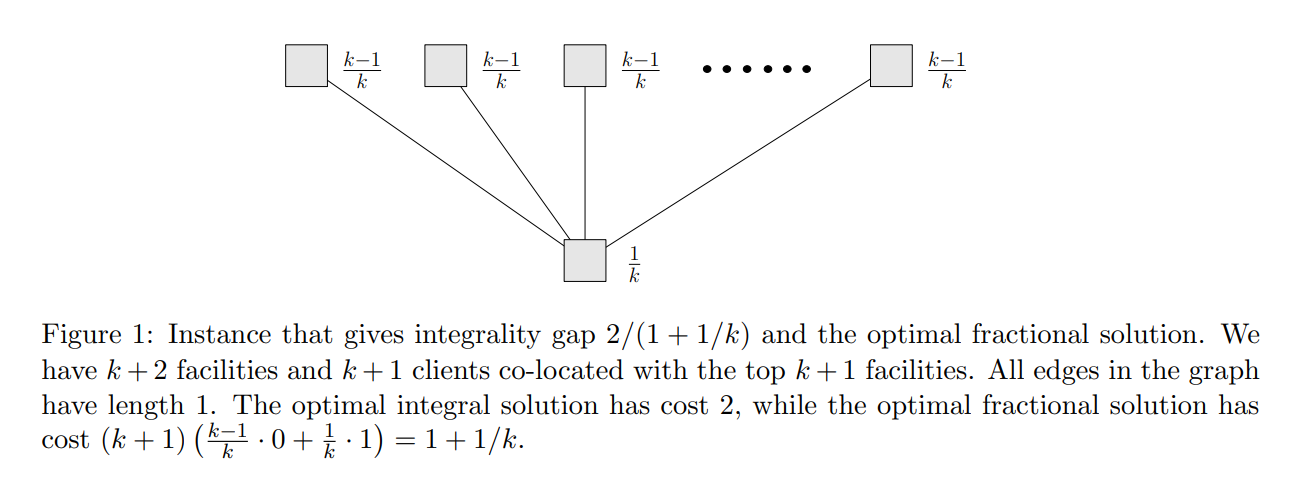
这篇文章的思路就是通过多开一些设施,使得整数最优解 opt 减少,但仍和开放 \(k\) 个的 LP 比较,这样会使得 integrality-gap 下降。如果允许开 \(k+1\) 个设施,那么上面这个星型图的整数最优解可以达到 0。考虑一些更复杂的情况,整个 instance 包含 2 个上面这样的星型,这样 LP 约为 2,可以在第一个星型中开放 \(k+1\) 个叶子,cost 为 0;在第二个星型中开放 \(k-2\) 个叶子以及中心,这样 cost 为 3。所以 integrality gap 为 \((0+3)/2=1.5\),可以看到多开放设施对于复杂的 instance 也可以降低 integrality gap。
JV 回顾

初始所有变量均为 0,令所有用户均为活跃状态,所有活跃用户的 \(v_j\) 均匀增加。
当 \(v_j\) 增加到 \(c_{ij}\) 时,称 \((i,j)\) 这条边变紧了。这个时候为了满足对偶规划的限制,增加 \(v_j\) 的同时也需要增加 \(w_{ij}\)。
当 \(w_{ij}\) 增加到一定程度时,会使得某些设施的限制 \(\sum_{j\in C}w_{ij}\le f_i\) 变紧,这个时候称设施 \(i\) 变紧,\(i\) 进入待开放状态。这个时候对 \(i\) 有贡献的用户 \(j\) (\(v_j\ge c_{ij}\))不能再继续增加,使得这些 \(j\) 变为不活跃。还可能出现一种情况是 \(i\) 变紧后,用户 \(j\) 因为对 \(i\) 还没有贡献仍然活跃,但当 \((i,j)\) 变紧时,接下来继续进行的话也会对 \(i\) 产生贡献,需要令 \(j\) 变为不活跃。
进行完这一阶段后,构建一个二分图 \(H(z)\),\(z\) 表示设施开放的成本。如果 \(w_{ij}>0\) 则将边 \((i,j)\) 加入 \(H(z)\)。再构建冲突图 \(G(z)\),这个图仅包含待开放设施,如果两个设施之间存在冲突边,当且仅当在 \(H(z)\) 中存在他们存在一个公共的邻居。JV 算法选择的是 \(G(z)\) 的一个极大独立集。(不一定是一个最大独立集)
使用 JV 算法解 k-median
JV 算法原文:https://dl.acm.org/doi/pdf/10.1145/375827.375845 P10
对于 k-median 引入拉格朗日乘子 \(\lambda\) 之后就变成了 UFL 问题。原 JV 算法的不连续性,导致了无法仅通过调整 \(\lambda\) 返回一组开放 \(k\) 个设施的解,所以使用 JV 算法得到一个 bi-point solution,之后再转化成一个整数解,转化成整数解会再损失一个 2-approx,所以是一个 6-approx。
通过 JV 算法得到两组解 \(S_{s},S_{l}\) 满足 \(k_1=|S_{s}|<k<|S_{l}|=k_2,ak_1+bk_2=k\),使用的拉格朗日乘子分别为 \(z_1,z_2\) 且满足 \(z_1>z_2\)。令 \(z_1-z_2<c_{\min}/12n_c^2\),其中 \(n_c\) 是客户点数量,\(c_{\min}\) 是最小的非零边长度。根据 JV 算法的性质,有
其中 cost 表示连接成本,\(\alpha\) 表示对偶解。
尝试将 \(cost(S_l)\le 3(\alpha_l-z_2k_2)\) 中的 \(z_2\) 替换成 \(z_1\):
将上式乘 \(b\) 加上 \(cost(S_s)\le 3(\alpha_s-z_1k_1)\) 乘 \(a\) 得:
其中 \(\alpha = a \alpha_s+b \alpha_l\)。
可以发现 bi-point solution 满足拉格朗日乘子为 \(z_1\) 的对偶规划(因为 \(z_1\) 是 \(z_1,z_2\) 中较大者,\(z\) 在对偶规划中用作上界)。
还需要说明 \(\alpha - k z_1 \le OPT\),其中 OPT 是 k-median 的最优解。
这是是因为 \(\alpha \le \text{Dual-LP} = \text{Primal-LP} \le OPT + k z_1\),其中第一个 \(\le\) 是因为对偶规划是一个最大化的规划,可行解不会超过最优解。第二个 \(\le\) 是因为 \(OPT + k z_1\) 是 facility location 的一个整数解,其不小于 LP 的值。
JV 的不连续性
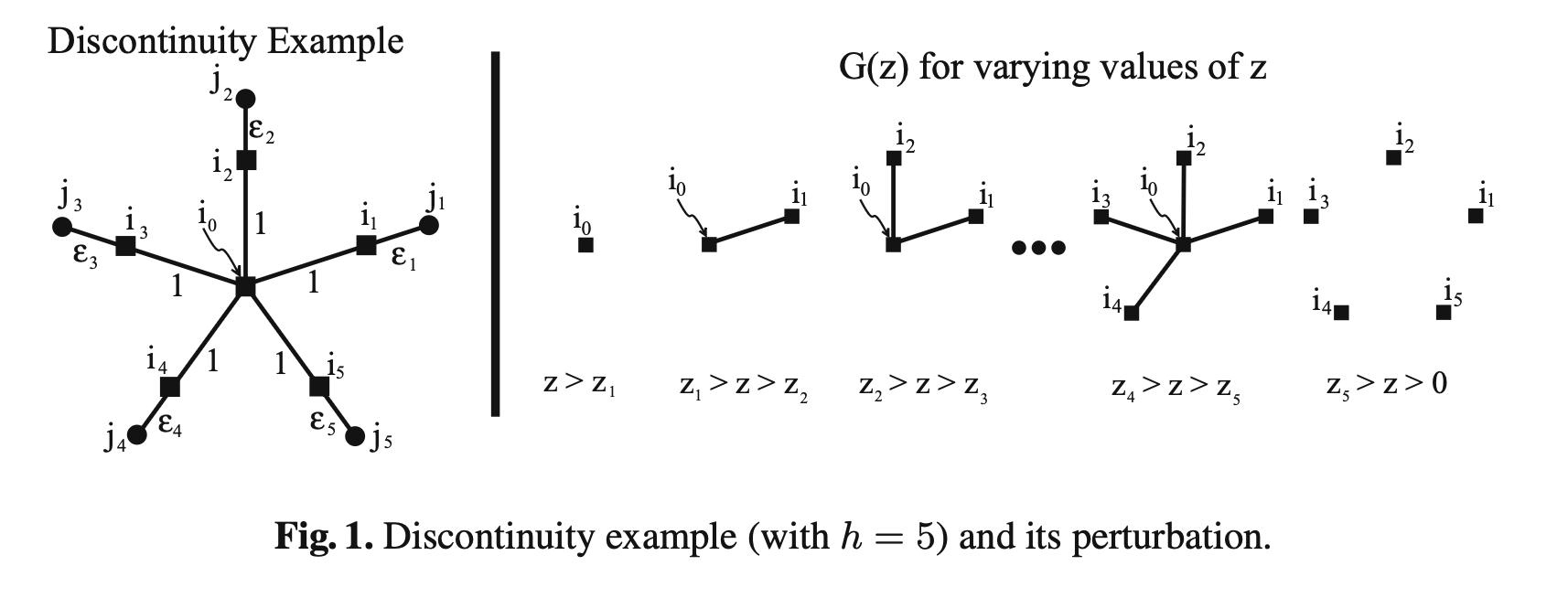
考虑上图左图,令所有的 \(\epsilon\) 均为 0,中心有一个设施,\(h\) 个 arm 端点上一个设施一个用户,到中心距离为 1。
那么当 \(z=z_0 = 1+\frac{1}{h-1}\) 时,开放中心的 cost 为 \(z_0+h = h+1+\frac{1}{h-1}\),开放 \(h\) 个 arm facility 时,cost 为 \(z_0h = h+\frac{h}{h-1}=h+1+\frac{1}{h-1}\)。所以当 \(z<z_0\) 时,会开放 \(h\) 个 facility;当 \(z>z_0\) 时,只开放中心的 1 个 facility。JV 的开放设施数量在 \(z_0\) 处不是连续的。
如果像上图那样给每个设施加一个偏移量,\(0=\epsilon_1<\dots<\epsilon_h\),那么会出现一系列的 critical value \(z_1,\dots,z_h\) 使得 \(z\) 每经过一个 critical value,开放设施的变化数量为 1,如上图右图。
退化性
定义在 JV 阶段一中边变紧和设施变紧为两种事件,如果一个 k-median 的 instance 是退化的,当且仅当存在一个时间点上至少有 3 个事件同时发生 或 至少两个时间点上有两个事件同时发生。
这篇文章将 k-median 的 instance 转化到 \(\mathbb R^{\mathcal C\times \mathcal F}_+\) 上,theorem3:
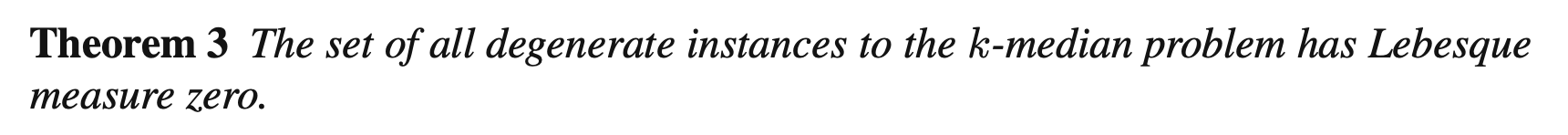
转化后退化的 instance 的测度为 0,应该就是不需要考虑退化的 instance 的意思。证明在全文版本中,但我并没有找到。
之后对于非退化的 instance 分析,这里的对 critical value 的正式定义为:使用该 value 作为开放成本进行算法,存在一个时间点,两个事件同时发生。

这里就是具体分析,当 \(z\) 越过一个 critical value 时,\(H(z)\) 会如何变化,\(G(z)\) 如何变化。因为只需要对非退化的 instance 分析,只需要分析六种情况。
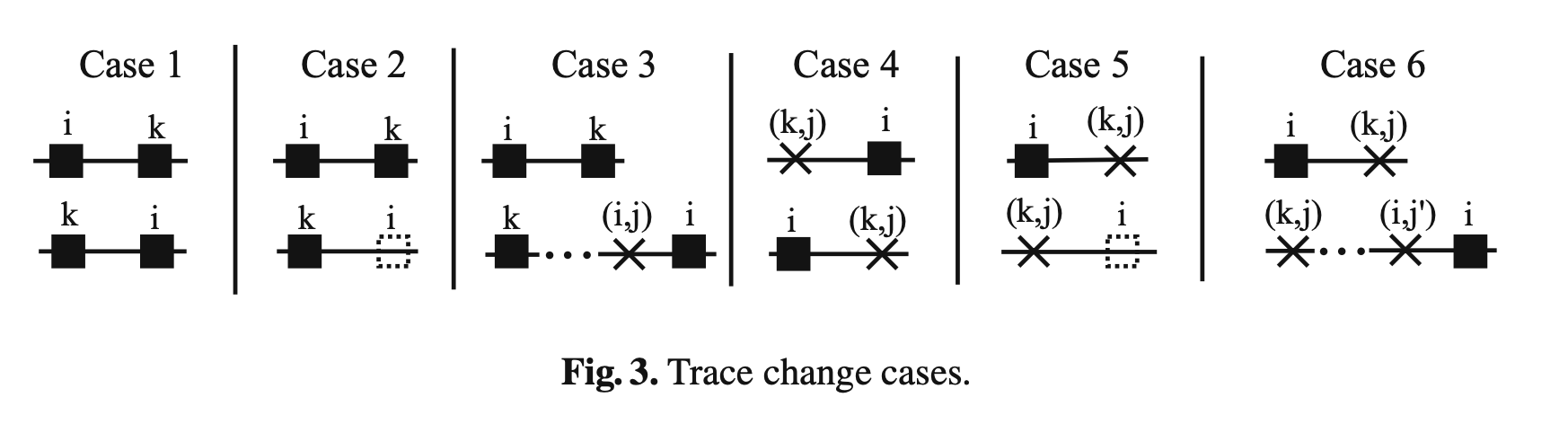
注意边变紧的时间都是在固定时刻的(如果可以变紧),设施变紧的时间受 \(z\) 的影响。
其中 case1 是说随着 z 的变化,两个设施变紧的时间的顺序发生了改变,这是由于对于不同的设施,对其有贡献的用户数量不同,增长率不同。
这几种情况的分析都是细节问题,不具体展开了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号