反射容斥
Part 0
有一张 \(n \times m\) 的网格图,每次只能向右或向上走,问从 \((0,0)\) 出发走到 \((n,m)\) 的方案数。
总共会走 \(n+m\) 步,选出 \(n\) 步向右走,方 案数即为 \(\binom{n+m}{n}\)。
Part 1
有一张 \(n \times m\) 的网格图,每次只能向右或向上走,问从 \((0,0)\) 出发走到 \((n,m)\) 且不接触到 \(y=x+1\) 直线的方案数。
考虑用总方案数减去接触到该直线的方案数,总方案数显然为 \(\binom{n+m}{n}\),只需求出接触到该直线的方案数即可。
考虑第一次接触到该直线的时候就将之后的路径与该直线对称,则最后到达的点即 \((m-1,n+1)\),方案数即为 \(\binom{n+m}{m-1}\)。
故方案数即为 \(\binom{n+m}{n}-\binom{n+m}{m-1}\)。
Part 2
将一条直线扩展为两条斜率为 \(1\) 的直线,仍然是从 \((0,0)\) 出发走到 \((n,m)\)。
若两条直线在 \((n,m)\) 同侧,则可视为一条限制,所以在此只考虑不在同一侧的情况。
不妨设上方的直线为 \(A:y=x+b1\),下方的直线为 \(B:y=x+b2\),终点为 \(P\)。
借用 Part 1 的思想考虑容斥,总方案依然为 \(\binom{n+m}{n}\)。考虑将不合法的路径接触直线 \(AB\) 的顺序写下来,大概为 \(A,B,AB,BA,AAB\cdots\),不妨将连续接触同一条直线缩成一次,则顺序为 \(A,B,AB,BA,\cdots\)。
有一个简单直观的容斥为:合法方案数=总方案数-序列开头为 \(A\) 的方案数-序列开头为 \(B\) 的方案数。
而开头为 \(A\) 的方案数似乎可以看成从 \((0,0)\) 走到 \(P\) 关于 \(A\) 的对称点的方案数?
发现不能这样简单的计算,因为这些方案还包括开头为 \(BA\) 的方案;同理,从 \((0,0)\) 走到 \(P\) 关于 \(B\) 的对称点的方案数也包括开头为 \(AB\) 的方案。同时减去这两项就会多减去开头为 \(AB\) 和 \(BA\) 的方案数,考虑如何求出这两项。
类比只接触一次的对称,以开头为 \(AB\) 举例,将路径接触 \(B\) 之后的一段沿 \(B\) 对称,然后将路径接触 \(A\) 之后的一段沿 \(A\) 对称(若先沿 \(A\) 对称会导致对称之后可能不接触 \(B\) 了)。
此时终点为 \(P\) 先沿 \(B\) 对称后沿 \(A\) 对称。发现此时仍然可能多记上开头为 \(BAB\) 的方案数,所以一直容斥下去直到终点不在第一象限即可。
发现我们每次向后加数,却是从后向前对称,不妨从结尾考虑,即:合法方案数=总方案数-结尾为 \(A\) 的方案数-结尾为 \(B\) 的方案数+\(\cdots\),此时就可以维护两个终点坐标,每次分别沿 \(A,B\) 对称,乘上容斥系数即可。
时间复杂度分析:发现每两次对称都会在经过终点的斜率为 \(-1\) 的直线上移动 \(b-c\) 的距离,所以时间复杂度为 \(\dfrac{n}{b-c}\)。
[SCOI2010] 生成字符串
模板题,设 \(dp_{i,j}\) 为左括号选了 \(i\) 个,右括号选了 \(j\) 个的方案数,则要求 \((i\ge j)\),求 \(dp_{n,m}\)。
转到网格图上,\(i \ge j\) 变为不接触 \(y=x+1\),变为 Part 1 内容。
Math Exam
解个方程,发现 \(a_1=1\),当 \(i\ge2\) 时,\(a_i=a_{i-1}+2\) 或 \(a_i=-a_{i-1}\),形式很不好看,经过神秘推导或神秘注意,设 \(b_i=\dfrac{|a_i+1|}{2}\),则有 \(b_0=0,b_1=1,b_i=b_{i-1}\pm 1\)。
此时发现是一维的,将 \(+\) 转化为向右走,\(-\) 转化为向上走,则根据绝对值与原题意的要求,有不接触直线 \(y=x+1\) 与 \(y=x-\dfrac{m+3}{2}\) 的要求,由于从 \((0,0)\) 出发,第一步只能向右走,所以 \(b_1\) 不必特殊处理。至此,此题转化为了 Part 2。
【集训队作业2018】count
此处有两个转化。
第一处转化参考 CF1748E,第二处转化考虑将笛卡尔树和括号序列结合。
首先有 \(n<m\) 无解。
其中 \(f_A(l,r)\) 为 \(A\) 序列的笛卡尔树上 \(l,r\) 的 \(lca\),则同构的条件即为两个序列的笛卡尔树形态相同。第一步转化为笛卡尔树形态计数。
设 \(F_u\) 为 \(u\) 子树内转化的括号序列,有 \(F_u=(F_{ls})F_{rs}\),设 \(dep_{u}\) 为 \(F_u\) 中括号最大嵌套深度,则 \(1 \sim m\) 的所有整数都在树中出现过的条件转化为 \(dep_{rt} \le m\)。
必要性:若 \(dep_{rt}> m\),则必须需要多于 \(m\) 个数才能填满整棵树。
充分性:由于有 \(n\ge m\),则令 \(a_{rt}=dep_{rt}\),最后选取若干条链将其权值增大微调即可。
则问题转化为对于整棵树形成的括号序列计数。
设 \(dp_{i,j}\) 为目前已经填了 \(i\) 个左括号与 \(j\) 个右括号的方案数,考虑约束有哪些。
首先由括号序列自身的 \(i \ge j\) 约束,而当前括号序列的深度可以转化为 \(i-j\),则还要求了 \(i-j \le m\),将 \(i\) 当作横坐标,\(j\) 当作纵坐标,转化到网格图上即为从 \((0,0)\) 出发,到达 \((n,n)\),不接触直线 \(y=x+1\) 与 \(y=x-(m+1)\) 的方案数。使用 Part 2 解决。
[JLOI2015] 骗我呢
发现值域为 \([0,m]\),则一行只有一个位置会 \(+2\),可以做出来简单 dp,优化过后变为 \(dp_{i,j}=dp_{i,j-1}+dp_{i-1,j+1}\)。
代数推导一点不会,组合意义天崩地裂。
考虑组合意义,将其放在网格图上,考虑将 dp 值变为到达 \((i,j)\) 的路径条数,dp 转移看为一条边。发现转移中有斜着的边,不好处理,所以将其平移。发现行末仍然有一条斜边,将其扩展为先向右再向下,于是得到一张网格图。由于将每一行行末扩展了,所以每一行长度为 \(m+1\),则问题变为在网格图上,从原点出发,到达 \((n+m+1,n)\) 的方案数。
如图:
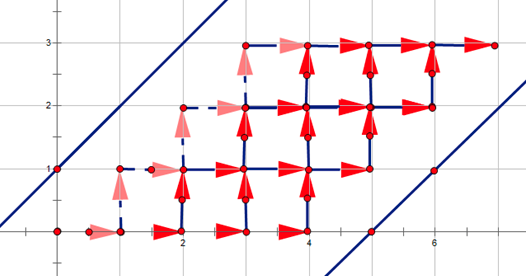
至此,将问题转化为了 Part 2,使用反射容斥即可线性求出答案。
[AGC070C] No Streak
先找直线的限制,发现只有一个即 A 胜场数始终大于等于 B 胜场数,则不妨设 \(f(a,b,x)\) 表示 A 胜了 \(a\) 场,B 胜了 \(b\) 场,平局了 \(x\) 场的方案数,将 \(a,b\) 当作坐标,则现在需要考虑的问题即为如何消去不接触 \(y=x+1\) 这条直线的限制。
发现如果直接按照 Part 1 中 \(ans=f(a,b,x)-f(b-1,a+1,x)\) 的式子(下文若无特殊说明,路径均指未对称的路径),不仅会多记录上第一次接触直线后仍然向上的路径(因为对称之后变成向上向右,从不合法变为合法了);还会少记录上第一次接触直线后向右的路径(因为对称之后变成连续两次向上,从合法变为不合法)。
发现合不合法都和第一次和直线接触后的移动强相关,所以分类讨论一下:
-
第一次接触直线后直接向右,对称后变成连续两次向上,所以不妨扣掉一次向上,即 \(f(b-1,a,x)\),最后在当前位置加上一次向上,形成双射。
-
第一次接触直线后停歇,此时可以任意走,仿照上述方法,扣掉一次停歇,即 \(f(b-1,a+1,x-1)\),但是会少计算上停上的情况,所以再减去扣掉一次停歇和向上的方案,即 \(f(b-1,a,x-1)\),与原路径形成双射。
最后的答案即为:\(f(b-1,a+1,x)-f(b-1,a,x)-f(b-1,a+1,x-1)-f(b-1,a,x-1)\)。
问题来到如何求出 \(f(a,b,x)\),由于每相邻的两个 a 之间都需要一个别的东西来隔开,所以枚举有 \(k\) 对 a 之间需要用 b 隔开,然后忽略 b,先只考虑只有 a 和 x 的情况,则 \(k\) 对 a 相邻的情况即为 \(\binom{a-1}{k}\)。
剩下的 \(a-1-k\) 个空都至少需要一个 x 隔开,而后剩下的 x 可以任意填在 \(a+1-k\) 个空中,使用插板法计算。
最后考虑 b,\(k\) 对相邻的 a 之间需要插入一个 b,剩下的 b 可以任意填在 \(a+1+x-k\) 个空中,但每个空至多填一个 b,依旧使用插板法计算即可。
最后得到:
本题需要对反射容斥的形态有深刻的理解。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号